| Time Limit: 5000MS | Memory Limit: 65536K | |
Description
There is a rectangular area containing n × m cells. Two cells are marked with “2”, and another two with “3”. Some cells are occupied by obstacles. You should connect the two “2”s and also the two “3”s with non-intersecting lines. Lines can run only vertically or horizontally connecting centers of cells without obstacles.
Lines cannot run on a cell with an obstacle. Only one line can run on a cell at most once. Hence, a line cannot intersect with the other line, nor with itself. Under these constraints, the total length of the two lines should be minimized. The length of a line is defined as the number of cell borders it passes. In particular, a line connecting cells sharing their border has length 1.
Fig. 1(a) shows an example setting. Fig. 1(b) shows two lines satisfying the constraints above with minimum total length 18.
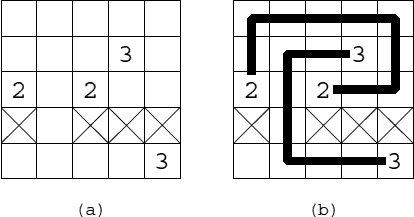
Figure 1: An example of setting and its solution
Input
The input consists of multiple datasets, each in the following format.
n m row1 … rown
n is the number of rows which satisfies 2 ≤ n ≤ 9. m is the number of columns which satisfies 2 ≤ m ≤ 9. Each rowi is a sequence of m digits separated by a space. The digits mean the following.
0:Empty
1:Occupied by an obstacle
2:Marked with “2”
3:Marked with “3”
The end of the input is indicated with a line containing two zeros separated by a space.
Output
For each dataset, one line containing the minimum total length of the two lines should be output. If there is no pair of lines satisfying the requirement, answer “0” instead. No other characters should be contained in the output.
Sample Input
5 5 0 0 0 0 0 0 0 0 3 0 2 0 2 0 0 1 0 1 1 1 0 0 0 0 3 2 3 2 2 0 0 3 3 6 5 2 0 0 0 0 0 3 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 2 3 0 5 9 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 2 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 9 9 3 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 3 9 9 0 0 0 1 0 0 0 0 0 0 2 0 1 0 0 0 0 3 0 0 0 1 0 0 0 0 2 0 0 0 1 0 0 0 0 3 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9 9 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 3 2 0 0
Sample Output
18 2 17 12 0 52 43
Source
#include<set> #include<queue> #include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> using namespace std; const int STATE = 59049+1000; const int Mod = 10007; #define For(i,n) for(int i=1;i<=n;i++) #define Rep(i,l,r) for(int i=l;i<=r;i++) #define Down(i,r,l) for(int i=r;i>=l;i--) struct statedp{ int head[Mod],next[STATE],f[STATE],state[STATE]; int size; void clear(){memset(head,-1,sizeof(head));size = 0;} void push(int st,int ans){ int Key = st % Mod; for(int p = head[Key];p!=-1;p=next[p]) if(st==state[p]){ f[p] = min(f[p],ans); return; } state[size] = st;f[size] = ans;next[size] = head[Key]; head[Key] = size++; } }dp[2]; int n,m,maze[12][12],code[12]; void init(){ For(i,n) For(j,m) scanf("%d",&maze[i][j]); } void dpblock(int i,int j,int cur){ int Lim = (j==m) ? (2) : (0); Rep(i,0,dp[cur].size-1) dp[cur^1].push(dp[cur].state[i] >> Lim , dp[cur].f[i]); } void shift(){ Down(i,m,1) code[i] = code[i-1];code[0] = 0; } int encode(){ int ret = 0; Rep(i,0,m) ret = ret << 2 | code[i]; return ret; } void decode(int st){ Down(i,m,0) code[i] = st & 3 , st >>= 2; } void dpblank(int i,int j,int cur){ Rep(k,0,dp[cur].size-1){ decode(dp[cur].state[k]); int Left = code[j-1] , Up = code[j]; if(maze[i][j]>=2){ if(Left&&Up) continue; int CODE = (maze[i][j]==2)?(1):2; if(Left||Up){ if(Left+Up!=CODE) continue; code[j-1] = code[j] = 0; if(j==m) shift(); dp[cur^1].push(encode(),dp[cur].f[k]); }else{ if(i<n && maze[i+1][j] != 1){ code[j-1] = CODE; code[j] = 0; if(j==m) shift(); dp[cur^1].push(encode(),dp[cur].f[k]); } if(j<m && maze[i][j+1] != 1){ code[j-1] = 0; code[j] = CODE; dp[cur^1].push(encode(),dp[cur].f[k]); } } continue; } if(Left && Up){ if(Left!=Up) continue; code[j-1] = code[j] = 0; if(j==m) shift(); dp[cur^1].push(encode(),dp[cur].f[k]+1); } else if(Left || Up){ int CODE = Left | Up; if(i<n && maze[i+1][j]!=1){ code[j-1] = CODE; code[j] = 0; if(j==m) shift(); dp[cur^1].push(encode(),dp[cur].f[k]+1); } if(j<m && maze[i][j+1]!=1){ code[j-1] = 0; code[j] = CODE; dp[cur^1].push(encode(),dp[cur].f[k]+1); } }else{ if(!maze[i][j]){ if(j==m) shift(); dp[cur^1].push(encode(),dp[cur].f[k]); } if(i<n && j<m && maze[i+1][j]!=1 && maze[i][j+1]!=1){ code[j-1] = code[j] = 1; dp[cur^1].push(encode(),dp[cur].f[k]+1); code[j-1] = code[j] = 2; dp[cur^1].push(encode(),dp[cur].f[k]+1); } } } } void DP(){ int cur = 0;dp[0].clear();dp[0].push(0,0); For(i,n) For(j,m){ dp[cur^1].clear(); if(maze[i][j]==1) dpblock(i,j,cur); else dpblank(i,j,cur); cur^=1; } int ans = 2147483647; Rep(i,0,dp[cur].size-1) ans = min(ans,dp[cur].f[i]); if(ans==2147483647) ans = -2; printf("%d ",ans+2); } int main(){ while(scanf("%d%d",&n,&m),m+n){ init(); DP(); } return 0; }