●赘述题目
算了,题目没有重复的必要。
注意理解:对答案造成贡献的是每个点,就是了。
举个栗子:
对于如下数据:
2 1
1 2 1
答案是 2;
●题解
方法:建图(难点)+最短路。
先来几个链接:(他们为我解题提供了思路,但有些部分看得我有点mengbi)
●http://blog.csdn.net/pure_w/article/details/55060079
●http://www.cnblogs.com/clrs97/p/5046933.html
●建图:
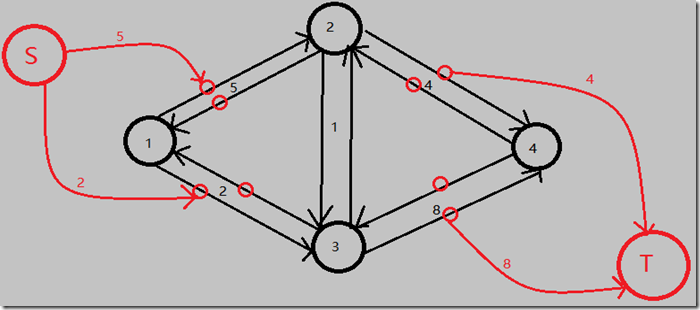
1.把原图的双向边拆成两条单向边(权值不变)。并把每条单向边看成一个点(称为新图点);
2.建立源点S,S向1号点的出边(新图点)建单向边,权值为那些出边的权值。
3.建立汇点T,n号点的入边(新图点)向T建单向边,权值为那些入边的权值。
效果如下:
接下来是比较暴力的建边
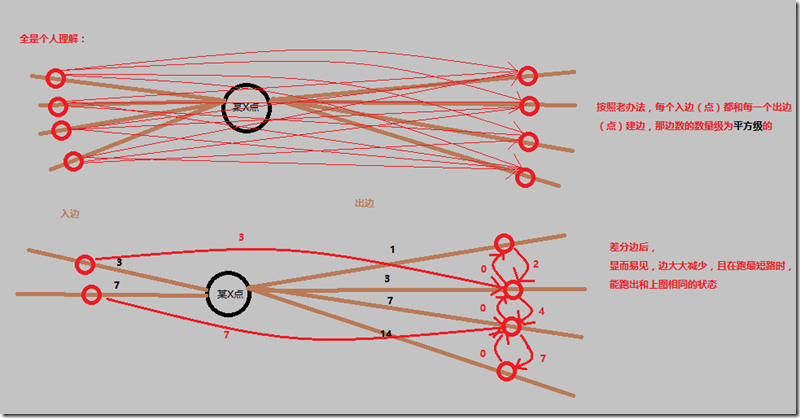
(4.)枚举每个原图点X,把它的每条入边(新图点)向每条出边(新图点)建边,权值为这两条出入边的较大权值。(这样导致边巨多)
然后是比较优化的建边
4.(似乎叫差分边),枚举每个原图点X,先把它的出边(新图点)从小到大排序,排序后相邻的出边(新图点)间建两条有向边,小的指向大的边权为两者权值之差,大的指向小的边权为0。再枚举它的每个入边(新图点),向该原图点X的与该入边(新图点)权值相同的出边建边(为什么一定存在权值相同的入边和出边呢?因为我们把无向边变成了两个有向边),权值就为该相同权值。
(4.)和4.的建图效果如下:
最后,新图已经建好,用4.建完图后,点和边的数量都可以接受,跑一个dijkstra就好啦!
●代码
#include<cstdio>
#include<cstring>
#include<queue>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
struct node{
int p;long long d;
bool operator <(const node &rtm) const {return d>rtm.d;}
};
struct edge{
int to,co,next;
}e[400005*2],E[2000000];
int headin[100005],headout[100005],head[400010],nextout[400005*2],nextin[400005*2];
int st[200005];
int n,m,dnt=2,ent=1,S,T,cnt,p;
ll dis[400010];
bool vis[400010];
bool cmp(int x,int y) {return e[x].co<e[y].co;}
void add(int u,int v,int c){
e[dnt]=(edge){v,c,0}; nextout[dnt]=headout[u];
e[dnt]=(edge){v,c,0}; nextin[dnt]=headin[v];
headout[u]=headin[v]=dnt++;
e[dnt]=(edge){u,c,0}; nextout[dnt]=headout[v];
e[dnt]=(edge){u,c,0}; nextin[dnt]=headin[u];
headout[v]=headin[u]=dnt++;
}
void ADD(int u,int v,int c) {E[ent]=(edge){v,c,head[u]}; head[u]=ent++;}
void make_something(int x){
cnt=0;
for(int i=headout[x];i;i=nextout[i]) st[++cnt]=i;
sort(st+1,st+cnt+1,cmp);
for(int i=1;i<cnt;i++) ADD(st[i],st[i+1],e[st[i+1]].co-e[st[i]].co),ADD(st[i+1],st[i],0);
for(int i=headin[x];i;i=nextin[i]) p=i^1,ADD(i,p,e[i].co);
}
void dijkstra(){
node u; int v;
memset(dis,0x7f,sizeof(dis));
priority_queue <node> q;
q.push((node){S,0}); dis[S]=0;
while(!q.empty()){
u=q.top(); q.pop();
if(vis[u.p]) continue; vis[u.p]=1;
for(int i=head[u.p];i;i=E[i].next){
v=E[i].to;
if(!vis[v]&&dis[v]>dis[u.p]+E[i].co){
dis[v]=dis[u.p]+E[i].co;
q.push((node){v,dis[v]});
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1,a,b,c;i<=m;i++) scanf("%d%d%d",&a,&b,&c),add(a,b,c);
// 建源点和汇点
S=dnt++; T=dnt++;
for(int i=headout[1];i;i=nextout[i]) ADD(S,i,e[i].co);
for(int i=headin[n];i;i=nextin[i]) ADD(i,T,e[i].co);
//枚举每一个原图点
for(int i=1;i<=n;i++) make_something(i);
dijkstra(); printf("%lld",dis[T]);
return 0;
}