Abstract
论文研究了卷积网络深度在大尺度图像识别设置中对其准确率的影响。主要贡献是使用一个带有非常小(3x3)卷积滤波器的架构对增加深度的网络进行了彻底的评估,这表明通过将深度推进到16 - 19个权重层,可以实现对先前art配置的显著改进。
Introduction
CNN取得重大成就离不开这三点:
- 大量的公开的公共数据集:large public image repositories, such as ImageNet
- 计算资源的大幅度提升(GPUs):high-performance computing systems, such as GPUs or large-scale distributed clusters
- 历届ILSVRC比赛的贡献:large-scale image classification systems
本文讨论了ConvNet架构设计的另一个重要方面—深度。
网络结构和配置
为了测量增加的对网络深度在一个公平的设置带来的改善,我们所有的受Ciresan等人的启发,ConvNet层的配置也采用了相同的原则。在本节中,我们首先描述ConvNet配置的一般布局(第2.1节),然后详细说明评估中使用的具体配置。
结构:
①在训练中,我们的是络一个固定大小的输入224×224 RGB图像。我们所做的唯一预处理是从每个像素中减去在训练集上计算的平均RGB值。
②在训练期间,我们的ConvNet的输入是固定大小的224×224 RGB图像。我们唯一的预处理是从每个像素中减去在训练集上计算的RGB均值。图像通过一堆卷积(conv.)层,我们使用感受野很小的滤波器:3×3(这是捕获左/右,上/下,中心概念的最小尺寸)。在其中一种配置中,我们还使用了1×1卷积滤波器,可以看作输入通道的线性变换(后面是非线性)。卷积步长固定为1个像素;卷积层输入的空间填充要满足卷积之后保留空间分辨率,即3×3卷积层的填充为1个像素。空间池化由五个最大池化层进行,这些层在一些卷积层之后(不是所有的卷积层之后都是最大池化)。在2×2像素窗口上进行最大池化,步长为2
③后面由5个max-pooling层执行,它们遵循一些conv层(不是所有conv层都遵循max-pooling)。Max-pooling是在一个22像素的窗口上执行的,步长为2。
一堆卷积层(在不同架构中具有不同深度)之后是三个全连接(FC)层:前两个每个都有4096个通道,第三个执行1000维ILSVRC分类,因此包含1000个通道(一个通道对应一个类别)。最后一层是soft-max层。所有网络中全连接层的配置是相同的。
④所有隐藏层均使用ReLU。
配置
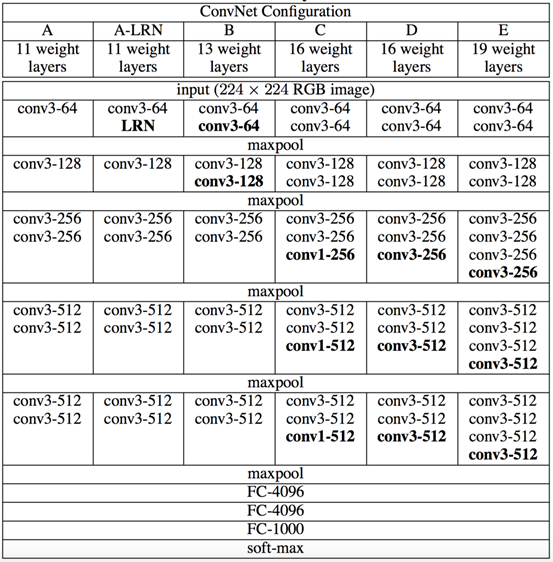
本文中评估的ConvNet配置在表1中列出,每列一个。接下来我们将按网络名称(A-E)来表示网络。所有配置都遵循2.1节提出的通用设计,并且仅是深度不同:从网络A中的11个加权层(8个卷积层和3个全连接层)到网络E中的19个加权层(16个卷积层和3个全连接层)。卷积层的宽度(通道数)相当小,从第一层中的64开始,然后在每个最大池化层之后增加2倍,直到达到512。
. ConvNet配置(以列显示)。随着更多的层被添加,配置的深度从左(A)增加到右(E)(添加的层以粗体显示)。卷积层参数表示为“conv⟨感受野大小⟩-⟨通道数⟩”。为了简洁起见,不显示ReLU激活功能。
网络的参数个数:
![]()
我们在整个网络使用非常小的3×3感受野,与输入的每个像素(步长为1)进行卷积。很容易看到两个3×3卷积层堆叠(没有空间池化)有5×5的有效感受野;三个这样的层具有7×7的有效感受野。那么我们获得了什么?例如通过使用三个3×3卷积层的堆叠来替换单个7×7层。首先,我们结合了三个非线性修正层,而不是单一的,这使得决策函数更具判别性。其次,我们减少参数的数量:假设三层3×3卷积堆叠的输入和输出有C个通道,堆叠卷积层的参数为3(32C2)=27C2个权重;同时,单个7×7卷积层将需要72C2=49C2个参数,即参数多81%。这可以看作是对7×7卷积滤波器进行正则化,迫使它们通过3×3滤波器(在它们之间注入非线性)进行分解。
结合1×1卷积层(配置C,表1)是增加决策函数非线性而不影响卷积层感受野的一种方式。即使在我们的案例下,1×1卷积基本上是在相同维度空间上的线性投影(输入和输出通道的数量相同),由修正函数引入附加的非线性。应该注意的是1×1卷积层最近在Lin等人(2014)的“Network in Network”架构中已经得到了使用。
训练图像大小:令S是等轴归一化的训练图像的最小边,ConvNet输入从S中裁剪(我们也将S称为训练尺度)。虽然裁剪尺寸固定为224×224,但原则上S可以是不小于224的任何值:对于S=224,裁剪图像将捕获整个图像的统计数据,完全扩展训练图像的最小边;对于S≫224,裁剪图像将对应于图像的一小部分,包含一个小对象或对象的一部分。
我们考虑两种方法来设置训练尺度S。第一种是修正对应单尺度训练的S(注意,采样裁剪图像中的图像内容仍然可以表示多尺度图像统计)。在我们的实验中,我们评估了以两个固定尺度训练的模型:S=256(已经在现有技术中广泛使用(Krizhevsky等人,2012;Zeiler&Fergus,2013;Sermanet等,2014))和S=384。给定一个ConvNet配置,我们首先使用S=256来训练网络。为了加速S=384网络的训练,用S=256预训练的权重来进行初始化,我们使用较小的初始学习率10−3。
设置S的第二种方法是多尺度训练,其中每个训练图像通过从一定范围[Smin,Smax](我们使用Smin=256和Smax=5122)随机采样S来单独进行归一化。由于图像中的目标可能具有不同的大小,因此在训练期间考虑到这一点是有益的。这也可以看作是通过尺度抖动进行训练集增强,其中单个模型被训练在一定尺度范围内识别对象。为了速度的原因,我们通过对具有相同配置的单尺度模型的所有层进行微调,训练了多尺度模型,并用固定的S=384进行预训练。
在测试时,给出训练的ConvNet和一个输入图像,它按以下方式分类。首先,将其等轴地归一化到预定义的最小图像边,表示为Q(我们也将其称为测试尺度)。我们注意到,Q不一定等于训练尺度S(正如我们在第4节中所示,每个S使用Q的几个值会改进性能)。然后,网络以类似于(Sermanet等人,2014)的方式密集地应用于归一化的测试图像上。即全连接层首先被转换成卷积层(第一FC层转换到7×7卷积层,最后两个FC层转换到1×1卷积层)。然后将所得到的全卷积网络应用于整个(未裁剪)图像上。结果是类得分图的通道数等于类别的数量,以及取决于输入图像大小的可变空间分辨率。最后,为了获得图像的类别分数的固定大小的向量,类得分图在空间上平均(和池化)。我们还通过水平翻转图像来增强测试集;将原始图像和翻转图像的soft-max类后验进行平均,以获得图像的最终分数。
由于全卷积网络被应用在整个图像上,所以不需要在测试时对采样多个裁剪图像(Krizhevsky等,2012),因为它需要网络重新计算每个裁剪图像,这样效率较低。同时,如Szegedy等人(2014)所做的那样,使用大量的裁剪图像可以提高准确度,因为与全卷积网络相比,它使输入图像的采样更精细。此外,由于不同的卷积边界条件,多裁剪图像评估是密集评估的补充:当将ConvNet应用于裁剪图像时,卷积特征图用零填充,而在密集评估的情况下,相同裁剪图像的填充自然会来自于图像的相邻部分(由于卷积和空间池化),这大大增加了整个网络的感受野,因此捕获了更多的上下文。虽然我们认为在实践中,多裁剪图像的计算时间增加并不足以证明准确性的潜在收益,但作为参考,我们还在每个尺度使用50个裁剪图像(5×5规则网格,2次翻转)评估了我们的网络,在3个尺度上总共150个裁剪图像,与Szegedy等人(2014)在4个尺度上使用的144个裁剪图像。
在这项工作中,我们评估了非常深的卷积网络(最多19个权重层)用于大规模图像分类。已经证明,表示深度有利于分类精度,并且深度大大增加的传统ConvNet架构(LeCun等,1989;Krizhevsky等,2012)可以实现ImageNet挑战数据集上的最佳性能。在附录中,我们还呈现了我们的模型很好地泛化到各种各样的任务和数据集上,可以匹敌或超越更复杂的识别流程,其构建围绕不深的图像表示。我们的结果再次证实了深度在视觉表示中的重要性。