#object: 研究元分析的调节效应
#writer: mike
#time: 2020,11,15
data <- read.csv("C:\Users\mike1\Desktop\大三人格与幸福感\dataOfTotal.csv",header = T,sep=",")
print(colnames(data))
#返回整体数据的缺失值的坐标
print(sum(is.na(data[,'内外倾'])))
#返回某一列数据的缺失值的坐标,这里没有纵坐标
print(which(is.na(data[,"内外倾"]),arr.ind = T))
#这是建立了一个副本,并且只有一列
data2 <- na.omit(data[,"内外倾"])
head(data2)
#删除一行数据,负数后面只能用数字表示,不能用字符串表示
data3 <- data[-15,]
print(rownames(data3))
library("meta")
#查看是否有缺失值
print(sum(is.na(data3[,"样本特征"])))
#查看数据的长度
length(data3[,"内外倾"])
#执行具体的函数,在这里变量不能有引号
res <- metacor(n=被试数,cor=内外倾,sm="ZCOR",byvar=样本特征,data=data3)
print(res)
#看组内某一个类别的效应的语句,注意subset的用法
res2 <- metacor(n=被试数,cor=内外倾,sm="ZCOR",data=data3,subset=样本特征=="大学生")
#也可以这样写 update(res,subset=subset=样本特征=="大学生"),得到同样的结果
print(res2)
#查看数据的某一行是否是类别变量
print(is.factor(data[,"样本特征"]))
#打印出具体的类别
print(factor(data[,"样本特征"]))
#或者是这样看
print(levels(data[,"样本特征"]))
#画出关于调节变量的回归系数的图
pdf(file="C:\users\mike1\desktop\forest3.pdf", width = 20, height = 20)
forest(res)
dev.off()
部分的结果:
COR 95%-CI %W(fixed) %W(random) 样本特征
1 0.5590 [0.4750; 0.6329] 1.8 2.5 中学生
2 0.4200 [0.3659; 0.4713] 5.8 2.8 大学生
3 0.3200 [0.1893; 0.4395] 1.2 2.3 中学生
4 0.3110 [0.2296; 0.3881] 3.1 2.7 大学生
5 0.3380 [0.1359; 0.5131] 0.5 1.8 大学生
6 0.2930 [0.1859; 0.3932] 1.8 2.5 大学生
7 0.2520 [0.1553; 0.3439] 2.3 2.6 大学生
8 0.3670 [0.2511; 0.4726] 1.4 2.4 大学生
9 0.4290 [0.3089; 0.5356] 1.2 2.3 大学生
10 0.2400 [0.0393; 0.4221] 0.6 1.8 中年人
11 0.3880 [0.3262; 0.4465] 4.7 2.8 中学生
12 0.2900 [0.1816; 0.3914] 1.8 2.5 大学生
13 0.2640 [0.1620; 0.3604] 2.1 2.6 大学生
14 0.1700 [0.0836; 0.2539] 3.1 2.7 大学生
15 0.3600 [0.3034; 0.4141] 5.8 2.8 大学生
16 0.4290 [0.3089; 0.5356] 1.2 2.3 大学生
17 0.4200 [0.3659; 0.4713] 5.8 2.8 大学生
18 0.4210 [0.3423; 0.4938] 2.8 2.7 大学生
19 0.3390 [0.1260; 0.5221] 0.5 1.7 大学生
20 0.2250 [0.1826; 0.2665] 12.1 2.9 中学生
21 0.2000 [0.0850; 0.3098] 1.7 2.5 中年人
22 0.3610 [0.2583; 0.4556] 1.8 2.5 中年人
23 0.6260 [0.5602; 0.6839] 2.3 2.6 中年人
24 0.2930 [0.1859; 0.3932] 1.8 2.5 大学生
25 0.4820 [0.3240; 0.6138] 0.7 2.0 大学生
26 0.1180 [0.0105; 0.2228] 2.0 2.6 中年人
27 0.3120 [0.2136; 0.4041] 2.1 2.6 大学生
28 0.4530 [0.3321; 0.5593] 1.2 2.3 老年人
29 0.2500 [0.1550; 0.3404] 2.4 2.6 中年人
30 0.2800 [0.1587; 0.3929] 1.5 2.4 大学生
31 0.1100 [0.0248; 0.1936] 3.2 2.7 大学生
32 0.4200 [0.3600; 0.4766] 4.7 2.8 大学生
33 0.2620 [0.1806; 0.3399] 3.2 2.7 大学生
34 0.2000 [0.1085; 0.2881] 2.7 2.7 中学生
35 0.6440 [0.5594; 0.7153] 1.3 2.4 老年人
36 0.1830 [0.0623; 0.2985] 1.6 2.5 大学生
37 0.1870 [0.0495; 0.3175] 1.2 2.3 大学生
38 0.3200 [0.1893; 0.4395] 1.2 2.3 中学生
39 0.1530 [0.0552; 0.2479] 2.4 2.6 中年人
40 0.2800 [0.1587; 0.3929] 1.5 2.4 大学生
Number of studies combined: k = 40
COR 95%-CI z p-value
Fixed effect model 0.3229 [0.3091; 0.3366] 42.69 0
Random effects model 0.3294 [0.2888; 0.3688] 14.93 < 0.0001
Quantifying heterogeneity:
tau^2 = 0.0174 [0.0111; 0.0328]; tau = 0.1319 [0.1054; 0.1811];
I^2 = 87.4% [83.8%; 90.2%]; H = 2.82 [2.49; 3.20]
Quantifying residual heterogeneity:
I^2 = 86.5% [82.4%; 89.7%]; H = 2.72 [2.38; 3.11]
Test of heterogeneity:
Q d.f. p-value
309.88 39 < 0.0001
Results for subgroups (fixed effect model):
k COR 95%-CI Q I^2
样本特征 = 大学生 25 0.3282 [0.3105; 0.3457] 109.13 78.0%
样本特征 = 老年人 2 0.5628 [0.4926; 0.6258] 7.68 87.0%
样本特征 = 中年人 7 0.2992 [0.2602; 0.3372] 94.83 93.7%
样本特征 = 中学生 6 0.2938 [0.2647; 0.3224] 55.55 91.0%
Test for subgroup differences (fixed effect model):
Q d.f. p-value
Between groups 42.69 3 < 0.0001
Within groups 267.18 36 < 0.0001
Results for subgroups (random effects model):
k COR 95%-CI tau^2 tau
样本特征 = 大学生 25 0.3176 [0.2774; 0.3566] 0.0092 0.0958
样本特征 = 老年人 2 0.5567 [0.3427; 0.7158] 0.0333 0.1823
样本特征 = 中年人 7 0.2910 [0.1284; 0.4384] 0.0490 0.2214
样本特征 = 中学生 6 0.3391 [0.2296; 0.4401] 0.0194 0.1393
Test for subgroup differences (random effects model):
Q d.f. p-value
Between groups 4.81 3 0.1859
Details on meta-analytical method:
- Inverse variance method
- DerSimonian-Laird estimator for tau^2
- Jackson method for confidence interval of tau^2 and tau
- Fisher's z transformation of correlations
从以上的结果中可以发现一个明显的问题,如果是固定效应那么 调节作用显著,也就是有组间差异,如果是随机效应,那么调节作用不显著,该怎么解释呢?
上面也有关于某一个组的效应的区间,
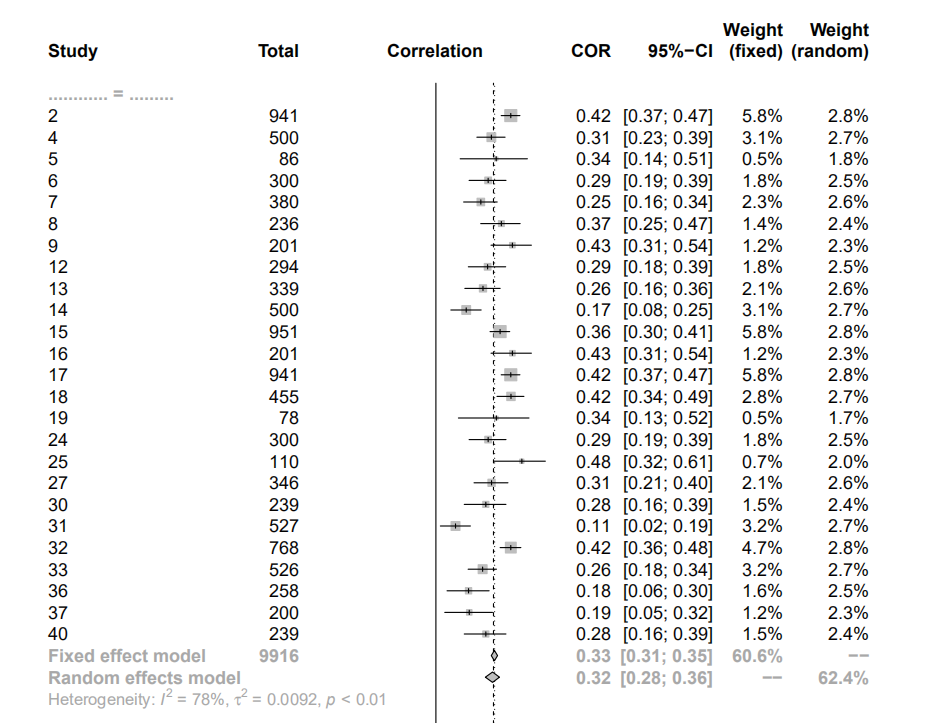
如果想看一个组的效应,也有相应的语句 res2 <- metacor(n=被试数,cor=内外倾,sm="ZCOR",data=data3,subset=样本特征=="大学生")
结果是:
COR 95%-CI %W(fixed) %W(random)
2 0.4200 [0.3659; 0.4713] 9.5 4.9
4 0.3110 [0.2296; 0.3881] 5.1 4.5
5 0.3380 [0.1359; 0.5131] 0.8 2.4
6 0.2930 [0.1859; 0.3932] 3.0 4.0
7 0.2520 [0.1553; 0.3439] 3.8 4.3
8 0.3670 [0.2511; 0.4726] 2.4 3.8
9 0.4290 [0.3089; 0.5356] 2.0 3.6
12 0.2900 [0.1816; 0.3914] 3.0 4.0
13 0.2640 [0.1620; 0.3604] 3.4 4.2
14 0.1700 [0.0836; 0.2539] 5.1 4.5
15 0.3600 [0.3034; 0.4141] 9.6 4.9
16 0.4290 [0.3089; 0.5356] 2.0 3.6
17 0.4200 [0.3659; 0.4713] 9.5 4.9
18 0.4210 [0.3423; 0.4938] 4.6 4.4
19 0.3390 [0.1260; 0.5221] 0.8 2.2
24 0.2930 [0.1859; 0.3932] 3.0 4.0
25 0.4820 [0.3240; 0.6138] 1.1 2.7
27 0.3120 [0.2136; 0.4041] 3.5 4.2
30 0.2800 [0.1587; 0.3929] 2.4 3.8
31 0.1100 [0.0248; 0.1936] 5.3 4.6
32 0.4200 [0.3600; 0.4766] 7.8 4.8
33 0.2620 [0.1806; 0.3399] 5.3 4.6
36 0.1830 [0.0623; 0.2985] 2.6 3.9
37 0.1870 [0.0495; 0.3175] 2.0 3.5
40 0.2800 [0.1587; 0.3929] 2.4 3.8
Number of studies combined: k = 25
COR 95%-CI z p-value
Fixed effect model 0.3282 [0.3105; 0.3457] 33.81 < 0.0001
Random effects model 0.3176 [0.2774; 0.3566] 14.64 < 0.0001
Quantifying heterogeneity:
tau^2 = 0.0092 [0.0038; 0.0192]; tau = 0.0958 [0.0616; 0.1385];
I^2 = 78.0% [68.0%; 84.9%]; H = 2.13 [1.77; 2.57]
Test of heterogeneity:
Q d.f. p-value
109.13 24 < 0.0001
Details on meta-analytical method:
- Inverse variance method
- DerSimonian-Laird estimator for tau^2
- Jackson method for confidence interval of tau^2 and tau
- Fisher's z transformation of correlations
这个结果相当于单纯的随机效应,固定效应。
图形