在解题过程中,我们有时需要维护一个数组的前缀和S[i]=A[1]+A[2]+...+A[i]。
但是不难发现,如果我们修改了任意一个A[i],则S[i]、S[i+1]、...、S[n]都会发生变化。
可以说,每次修改A[i]后,调整前缀和S[]在最坏情况下会需要O(n)的时间。当n非常大时,程序会运行得非常缓慢。
因此,这里我们引入“树状数组”,它的修改与求和都是O(logn)的,效率非常高。
树状数组的结构如下所示(注意数组下标从1开始,这点会影响到各函数的实现):
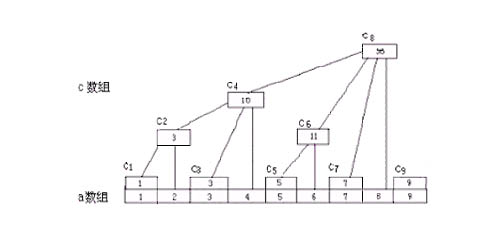
对于每颗子树Cn,它表示A[i-2^k+1]到A[i]的和,而k则是i在二进制时末尾0的个数,或者说是i用2的幂方和表示时的最小指数。而2^k则表示i的二进制表示中最右边的二进制1及末尾的所有0所表示的数。比如10100代表的是十进制的20,则它的子树是[10100-100+1,10100]。
一、C[i]子树结点数2^k的求法
C[i]子树的终止结点是i,开始结点可以看作是把i的最末一个1置零并加上1的结点。
int Lowbit(int x)
{
return x & ( x ^ ( x - 1 ) );
/*
注意到我们需要得到x的最后的1及之后的0不变且最后的1的高位取反的值,也可由-x = ~x+1得到
return x&(-x);
*/
}二、求数组前缀和S[i]
传统的数组前缀求和是将从A[0]到A[i]的数相加。利用树状数组,只需将多个子树的根相加。
对于前缀和S[i],首先加上以i为根的子树和C[i],然后减去这个子树(相当于把i的二进制最末一个1置为0)并迭代求前缀和S[i-2^k]。
int Sum(int end)
{
int sum = 0;
while(end > 0)
{
sum += C[end];
end -= Lowbit(end); //end &= (end-1);等价于将end的最末一个1置为0;
}
return sum;
} 三、当数组中的元素有变更时,需要更新A[i]所在的所有子树的根节点值。
首先更新C[i]子树的值,C[i]的父节点的下标可看作是i加上它的兄弟子树的元素个数,而它的兄弟子树与它的元素个数相同,都是Lowbit(i)。如此迭代i = i + Lowbit(i)直到i大于n。在O(logn)步能更新树状数组的值。
void Change(int pos , int num)
{
while(pos <= n)
{
C[pos] += num;
pos += Lowbit(pos);
}
}