A soldier wants to buy w bananas in the shop. He has to pay k dollars for the first banana, 2k dollars for the second one and so on (in other words, he has to pay i·k dollars for the i-th banana).
He has n dollars. How many dollars does he have to borrow from his friend soldier to buy w bananas?
The first line contains three positive integers k, n, w (1 ≤ k, w ≤ 1000, 0 ≤ n ≤ 109), the cost of the first banana, initial number of dollars the soldier has and number of bananas he wants.
Output one integer — the amount of dollars that the soldier must borrow from his friend. If he doesn't have to borrow money, output 0.
3 17 4
13
题意:第i个香蕉i*k元 买w个香蕉 现在有n元 问需要借多少钱?
题解:k*(1+w)*w/2-n
1 //code by drizzle 2 #include<bits/stdc++.h> 3 #include<iostream> 4 #include<cstring> 5 #include<cstdio> 6 #include<algorithm> 7 #include<vector> 8 #define ll __int64 9 #define PI acos(-1.0) 10 #define mod 1000000007 11 using namespace std; 12 int k,n,w; 13 int main() 14 { 15 scanf("%d %d %d",&k,&n,&w); 16 if(k*(1+w)*w/2-n<0) 17 cout<<"0"<<endl; 18 else 19 cout<<k*(1+w)*w/2-n<<endl; 20 return 0; 21 }
Colonel has n badges. He wants to give one badge to every of his n soldiers. Each badge has a coolness factor, which shows how much it's owner reached. Coolness factor can be increased by one for the cost of one coin.
For every pair of soldiers one of them should get a badge with strictly higher factor than the second one. Exact values of their factors aren't important, they just need to have distinct factors.
Colonel knows, which soldier is supposed to get which badge initially, but there is a problem. Some of badges may have the same factor of coolness. Help him and calculate how much money has to be paid for making all badges have different factors of coolness.
First line of input consists of one integer n (1 ≤ n ≤ 3000).
Next line consists of n integers ai (1 ≤ ai ≤ n), which stand for coolness factor of each badge.
Output single integer — minimum amount of coins the colonel has to pay.
4
1 3 1 4
1
5
1 2 3 2 5
2
In first sample test we can increase factor of first badge by 1.
In second sample test we can increase factors of the second and the third badge by 1.
题意:n个数 现在要求这n个数完全不同 并且对于单个数只能增加x或不变
问min(Σ x)
题解:标记每个数的个数 从i=1开始遍历 因为要求每个数只能出现一次所以 对于其余的数
全部加1继承到下一个数 并且更新ans 一直遍历到i=2*3000; 考虑3000个3000的特殊数据;
1 //code by drizzle 2 #include<bits/stdc++.h> 3 #include<iostream> 4 #include<cstring> 5 #include<cstdio> 6 #include<algorithm> 7 #include<vector> 8 #define ll __int64 9 #define PI acos(-1.0) 10 #define mod 1000000007 11 using namespace std; 12 int n; 13 int a[3005]; 14 int mp[6010]; 15 int main() 16 { 17 scanf("%d",&n); 18 memset(mp,0,sizeof(mp)); 19 for(int i=1;i<=n;i++) 20 { 21 scanf("%d",&a[i]); 22 mp[a[i]]++; 23 } 24 int ans=0; 25 for(int i=1;i<=6005;i++) 26 { 27 if(mp[i]>1) 28 { 29 ans+=(mp[i]-1); 30 mp[i+1]+=(mp[i]-1); 31 } 32 } 33 cout<<ans<<endl; 34 return 0; 35 }
Two bored soldiers are playing card war. Their card deck consists of exactly n cards, numbered from 1 to n, all values are different. They divide cards between them in some manner, it's possible that they have different number of cards. Then they play a "war"-like card game.
The rules are following. On each turn a fight happens. Each of them picks card from the top of his stack and puts on the table. The one whose card value is bigger wins this fight and takes both cards from the table to the bottom of his stack. More precisely, he first takes his opponent's card and puts to the bottom of his stack, and then he puts his card to the bottom of his stack. If after some turn one of the player's stack becomes empty, he loses and the other one wins.
You have to calculate how many fights will happen and who will win the game, or state that game won't end.
First line contains a single integer n (2 ≤ n ≤ 10), the number of cards.
Second line contains integer k1 (1 ≤ k1 ≤ n - 1), the number of the first soldier's cards. Then follow k1 integers that are the values on the first soldier's cards, from top to bottom of his stack.
Third line contains integer k2 (k1 + k2 = n), the number of the second soldier's cards. Then follow k2 integers that are the values on the second soldier's cards, from top to bottom of his stack.
All card values are different.
If somebody wins in this game, print 2 integers where the first one stands for the number of fights before end of game and the second one is 1 or 2 showing which player has won.
If the game won't end and will continue forever output - 1.
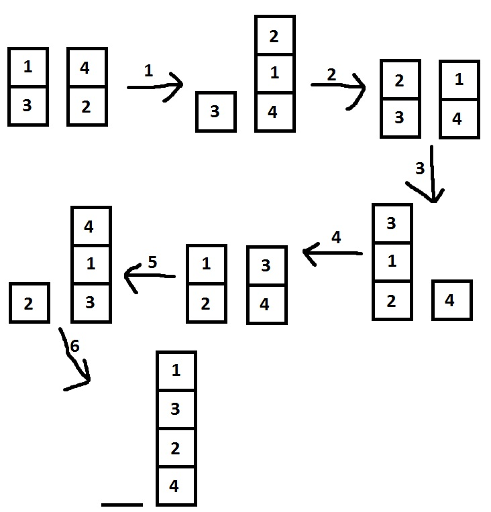
4
2 1 3
2 4 2
6 2
3
1 2
2 1 3
-1
First sample:
Second sample
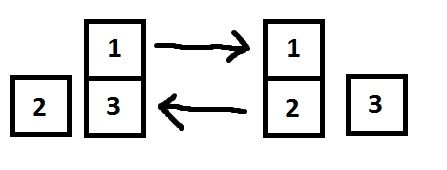
题意: 给你初始两个队列 q1 q2 两个队头元素出队x y 比较大小 x>y y,x按照顺序入q1 反之亦然;
不存在x,y相等的情况
当某一个队列为空时 另一个队列获胜 输出游戏进行的回合数和获胜一方的编号1或2
若游戏一直进行无法结束输出-1;
题解:队列模拟整个过程 对于死循环的判断 设置一个回合进行的上限值 超过上限则break 输出-1;
1 //code by drizzle 2 #include<bits/stdc++.h> 3 #include<iostream> 4 #include<cstring> 5 #include<cstdio> 6 #include<algorithm> 7 #include<vector> 8 #define ll __int64 9 #define PI acos(-1.0) 10 #define mod 1000000007 11 using namespace std; 12 int n; 13 int k1,k2; 14 queue<int> q1; 15 queue<int> q2; 16 int exm; 17 int main() 18 { 19 scanf("%d",&n); 20 scanf("%d",&k1); 21 while(!q1.empty()) 22 q1.pop(); 23 while(!q2.empty()) 24 q2.pop(); 25 for(int i=1;i<=k1;i++) 26 { 27 scanf("%d",&exm); 28 q1.push(exm); 29 } 30 scanf("%d",&k2); 31 for(int i=1;i<=k2;i++) 32 { 33 scanf("%d",&exm); 34 q2.push(exm); 35 } 36 int ans=0; 37 int out=0; 38 int flag=1; 39 while(flag) 40 { 41 if(ans>500000) 42 { 43 cout<<"-1"<<endl; 44 return 0; 45 } 46 if(q1.empty()) 47 { 48 flag=0; 49 out=2; 50 } 51 if(q2.empty()) 52 { 53 flag=0; 54 out=1; 55 } 56 if(flag==0) 57 break; 58 ans++; 59 int x=q1.front(),y=q2.front(); 60 q1.pop(); 61 q2.pop(); 62 if(x<y) 63 { 64 q2.push(x); 65 q2.push(y); 66 } 67 else 68 { 69 q1.push(y); 70 q1.push(x); 71 } 72 } 73 printf("%d %d ",ans,out); 74 return 0; 75 }