前面几篇关于数据库底层磁盘文件读取,数据库索引实现细节进行了深入的研究,但是没有串联起来的讲解为什么数据库索引会采用B树和B+树而不是其他的数据结构,例如平衡二叉树、链表等,因此,本文打算从数据库文件存储以及读取说起,讲解数据库索引的由来。
我们以抛出问题的形式开始讲解:
(1)数据库文件存储的方式
数据库文件存储都是以磁盘文件存储在系统中的,这也是数据库能持久化存储数据的原因。
(2)从数据库读取数据的原理
从数据库读取数据,先暂且不考虑从缓存中读取数据的情况,那就是从磁盘文件中读取数据的,我们知道从磁盘文件中读取数据是比较耗时的,数据库的select操作的时间,取决于执行磁盘IO的次数,因此尽量减少磁盘IO就可以显著的提升数据的查询速度。
(3)减少磁盘IO操作的影响因素
有哪些因素可以减少磁盘IO呢,这首先得将了解一下磁盘IO与预读。
磁盘IO与预读
磁盘读取依靠的是机械运动,分为寻道时间、旋转延迟、传输时间三个部分,这三个部分耗时相加就是一次磁盘IO的时间,大概9ms左右。这个成本是访问内存的十万倍左右;正是由于磁盘IO是非常昂贵的操作,所以计算机操作系统对此做了优化:预读;每一次IO时,不仅仅把当前磁盘地址的数据加载到内存,同时也把相邻数据也加载到内存缓冲区中。因为局部预读原理说明:当访问一个地址数据的时候,与其相邻的数据很快也会被访问到。每次磁盘IO读取的数据我们称之为一页(page)。一页的大小与操作系统有关,一般为4k或者8k。这也就意味着读取一页内数据的时候,实际上发生了一次磁盘IO。
正因为有了磁盘IO预读机制,所以才有了减少磁盘IO的可能,因为一次磁盘IO操作,可以查找到物理存储中相邻的一大片数据。
以索引为B+树为例:
磁盘IO次数和索引数据结构查询的次数以及磁盘IO与预读都有关系,具体关系:磁盘IO次数 <= B+树中从根节点一直到叶子节点整个过程中查询的节点数。
一次磁盘IO操作可以取出物理存储中相邻的一大片数据,如果查询的索引数据(就是B+树中从根节点一直到叶子节点整个过程中查询的节点数)都集中在该区域,那么只需要一次磁盘IO,否则就需要多次磁盘IO
(4)基于磁盘IO预读机制,索引可以快速查询数据
到现在才开始讲解索引了。正是基于磁盘IO预读机制的前提,数据库可以采用索引机制快速查询出数据。
(a)什么是索引
索引是帮助数据高效查询数据的一种数据结构,它包含一个表中某些列的值以及记录对应的地址,并且把这些值存储在一个数据结构中。常用的索引有B树和B+树
(b)为什么要使用索引
举个例子来说,假设我们有一个数据库student,这个表分别有三个字段:name,age,class。假设表中有2000条记录。
1、假如没有使用索引,当我们查询名为“xiaxia”的学生的时候,即调用:
select name,age,class from student where name = "xiaxia";
此时数据库不得不在student表中对这2000条记录一条一条的进行判断name字段是否为“xiaxia”。这也就是所谓的全表扫描。
2、而当我们在student表上的name字段上创建索引时,当我们查询名为“xiaxia”的学生时:
会通过索引查找去查询名为“xiaxia”的学生,因为该索引已经按照字母顺序排列,因此要查找名为“xiaxia”的记录时会快很多,因为名字首字母为“x”的雇员都是排列在一起的。通过该索引,能获取到表中对应的记录。
(5)数据库中使用什么数据结构作为索引
(a)链表
链表的查询速度是O(N),每次查询都得从链表头开始查询,例如上面查询“xiaxia”,如果xiaxia在1000的位置,那么需要遍历1000次才能查找到。
(b)数组
有人可能会说,查询速度肯定是数据最快呀,毕竟O(1),的确单纯就select的话,采用数组的形式是最合适的,但是采用数组会遇到如下几个问题:1、采用数组的话,其他操作如Delete、Update、Insert就不合适了;2、另外一个原因:索引是存在于磁盘中,当索引非常大的时候,达到几个G的时候,无法一次加载到内存中。
(c)平衡二叉树
二叉查找树查询的时间复杂度是O(logN),查找速度最快和比较次数最少,既然性能已经如此优秀,但为什么实现索引是使用B-Tree而不是二叉查找树,关键因素是磁盘IO的次数。
(d)B树和B+树
数据库索引采用的数据结构
(6)采用平衡二叉树和B树,数据查询的对比
这里直接引用https://blog.csdn.net/sinat_27602945/article/details/80118362,感谢博主。
二叉树查询过程:
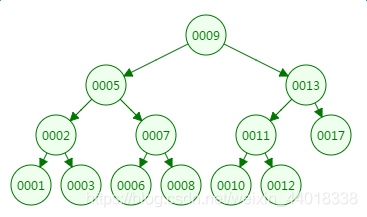
我们先来看二叉树查找时磁盘IO的次:定义一个树高为4的二叉树,查找值为10:
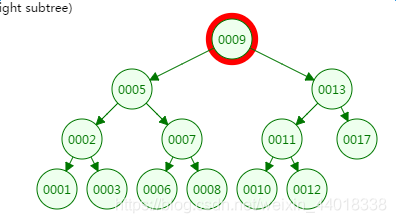
第一次磁盘IO:
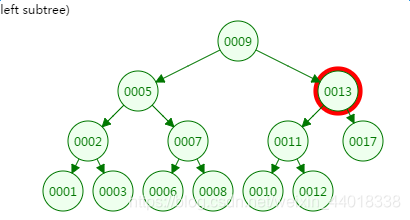
第二次磁盘IO
第三次磁盘IO:
第四次磁盘IO:
从二叉树的查找过程了来看,树的高度和磁盘IO的次数都是4,所以最坏的情况下磁盘IO的次数由树的高度来决定。
从前面分析情况来看,减少磁盘IO的次数就必须要压缩树的高度,让瘦高的树尽量变成矮胖的树,所以B-Tree就在这样伟大的时代背景下诞生了。
B-Tree查询过程:
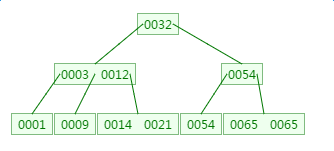
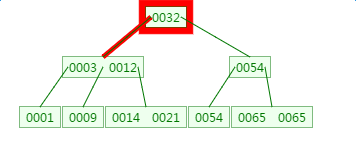
如下有一个3阶的B树,观察查找元素21的过程:
第一次磁盘IO:
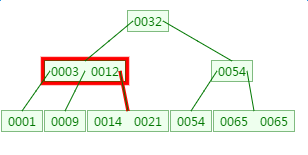
第二次磁盘IO:
这里有一次内存比对:分别跟3与12比对
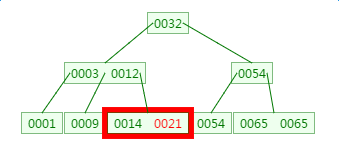
第三次磁盘IO:
B树的查询次数少于平衡二叉树!所以基于B树以及B+树的查询次数少于平衡二叉树。
关于B+树的具体讲解,可以参照前面的博客:漫画叙述B+树和B-树,很值得看!