主成分分析
一、理论部分
- 主成分分析
- 无监督学习
- 背景:当变量数量多的时候,很难通过可视化看到4维及以上的变量的关系
- 保留原始数据中尽可能多的信息,保留最小数据空间——解决方法:主成分分析(数据降维)
- 主成分分析:一种将原始数据投影到低维线性空间上的降维技术;将一组相关变量转换到一组新的不相关变量中
- 求解主成分:数据间变化比较大的方向->得到特征向量即是解
- 使用范围:有相关性,可用PCA进行降维
- 碎石图
- 显示每个主成分的方差,可以用来选择数据可以使用多少个主成分。
- 寻找拐点,拐点之后表示增加主成分的数量不会增加解释的方差量。
二、实践部分
# 添加目录到系统路径方便导入模块,该项目的根目录为".../machine-learning-toy-code"
import sys
from pathlib import Path
curr_path = str(Path().absolute())
parent_path = str(Path().absolute().parent)
p_parent_path = str(Path().absolute().parent.parent)
sys.path.append(p_parent_path)
print(f"主目录为:{p_parent_path}")
主目录为:c:\Users\……\12月sklearn学习\machine-learning-toy-code
from torch.utils.data import DataLoader
from torchvision import datasets
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt
train_dataset = datasets.MNIST(root = p_parent_path+'/datasets/', train = True,transform = transforms.ToTensor(), download = False)
test_dataset = datasets.MNIST(root = p_parent_path+'/datasets/', train = False,
transform = transforms.ToTensor(), download = False)
batch_size = len(train_dataset)
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=True)
X_train,y_train = next(iter(train_loader))
X_test,y_test = next(iter(test_loader))
X_train,y_train = X_train.cpu().numpy(),y_train.cpu().numpy() # tensor转为array形式)
X_test,y_test = X_test.cpu().numpy(),y_test.cpu().numpy() # tensor转为array形式)
X_train = X_train.reshape(X_train.shape[0],784)
X_test = X_test.reshape(X_test.shape[0],784)
m , p = X_train.shape # m:训练集数量,p:特征维度数
print(f"原本特征维度数:{p}") # 特征维度数为784
原本特征维度数:784

得到m=60000,p=784
# n_components是>=1的整数时,表示期望PCA降维后的特征维度数
# n_components是[0,1]的数时,表示主成分的方差和所占的最小比例阈值,PCA类自己去根据样本特征方差来决定降维到的维度
model = PCA(n_components=0.95)
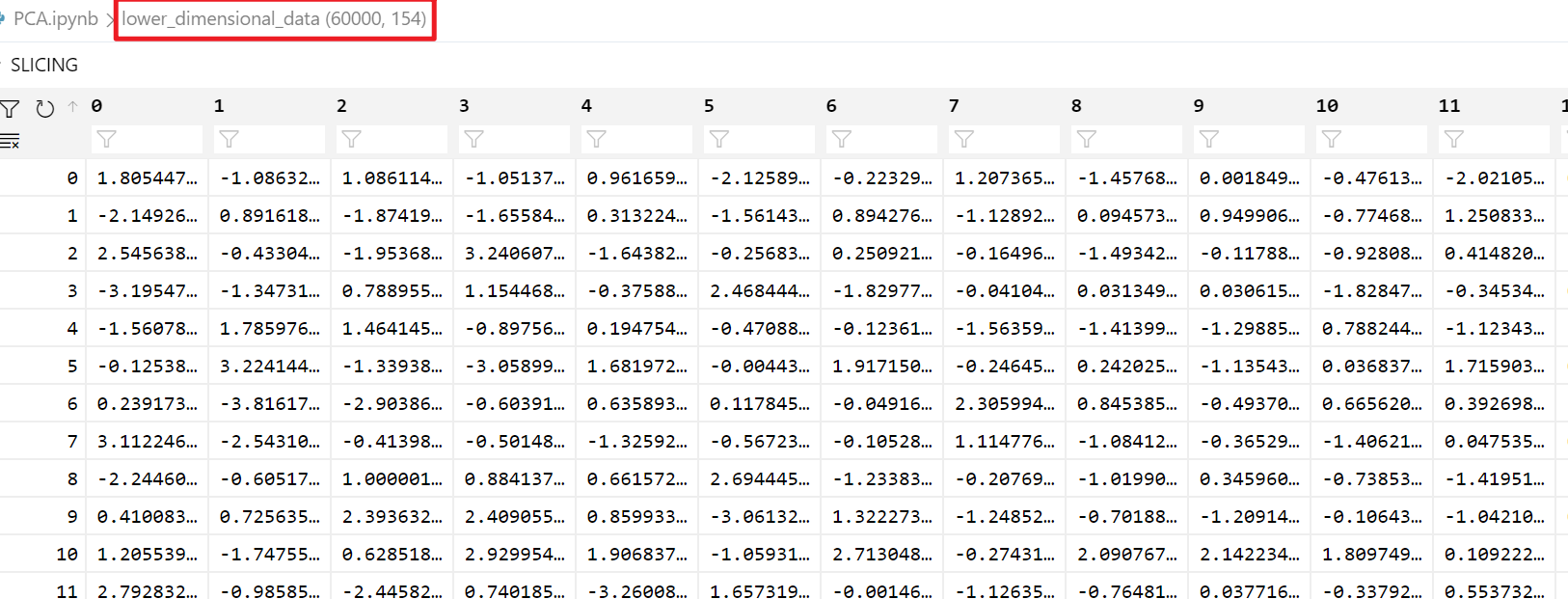
lower_dimensional_data = model.fit_transform(X_train)
print(f"降维后的特征维度数:{model.n_components_}")
降维后的特征维度数:154
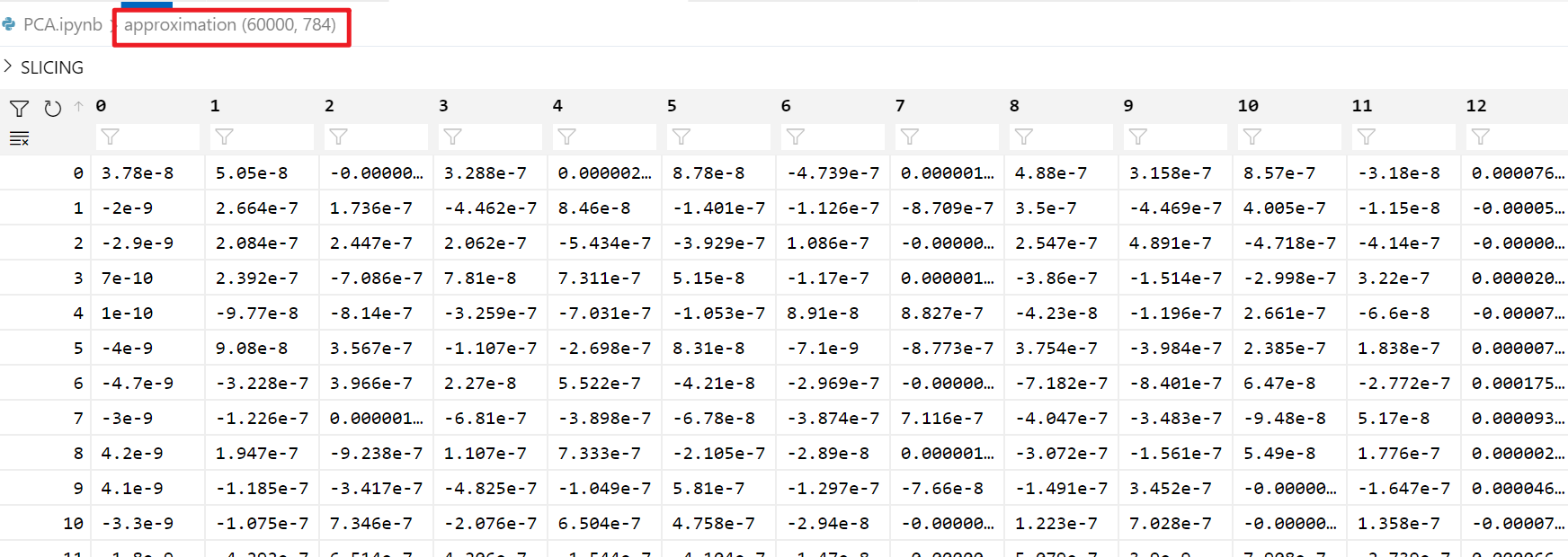
approximation = model.inverse_transform(lower_dimensional_data) # 降维后的数据还原
plt.figure(figsize=(8,4));
# 原始图片
plt.subplot(1, 2, 1);
plt.imshow(X_train[1].reshape(28,28),
cmap = plt.cm.gray, interpolation='nearest',
clim=(0, 1));
plt.xlabel(f'{X_train.shape[1]} components', fontsize = 14)
plt.title('Original Image', fontsize = 20)
# 降维后的图片
plt.subplot(1, 2, 2);
plt.imshow(approximation[1].reshape(28, 28),
cmap = plt.cm.gray, interpolation='nearest',
clim=(0,1));
plt.xlabel(f'{model.n_components_} components', fontsize = 14)
plt.title('95% of Explained Variance', fontsize = 20)
plt.show()

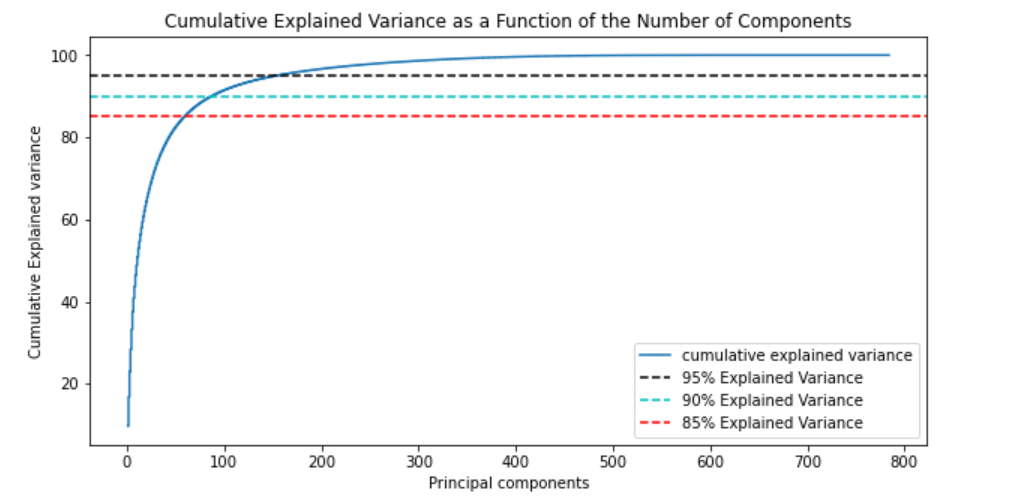
不同主成分个数对应的可解释方差分析(Explained Variance)
model = PCA() # 这里需要分析所有主成分,所以不降维
model.fit(X_train)
tot = sum(model.explained_variance_)
var_exp = [(i/tot)*100 for i in sorted(model.explained_variance_, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
plt.figure(figsize=(10, 5))
plt.step(range(1, p+1), cum_var_exp, where='mid',label='cumulative explained variance') # p:特征维度数
plt.title('Cumulative Explained Variance as a Function of the Number of Components')
plt.ylabel('Cumulative Explained variance')
plt.xlabel('Principal components')
plt.axhline(y = 95, color='k', linestyle='--', label = '95% Explained Variance')
plt.axhline(y = 90, color='c', linestyle='--', label = '90% Explained Variance')
plt.axhline(y = 85, color='r', linestyle='--', label = '85% Explained Variance')
plt.legend(loc='best')
plt.show()
def explained_variance(percentage, images):
'''
:param: percentage [float]: 降维的百分比
:return: approx_original: 降维后还原的图片
:return: model.n_components_: 降维后的主成分个数
'''
model = PCA(percentage)
model.fit(images)
components = model.transform(images)
approx_original = model.inverse_transform(components)
return approx_original,model.n_components_
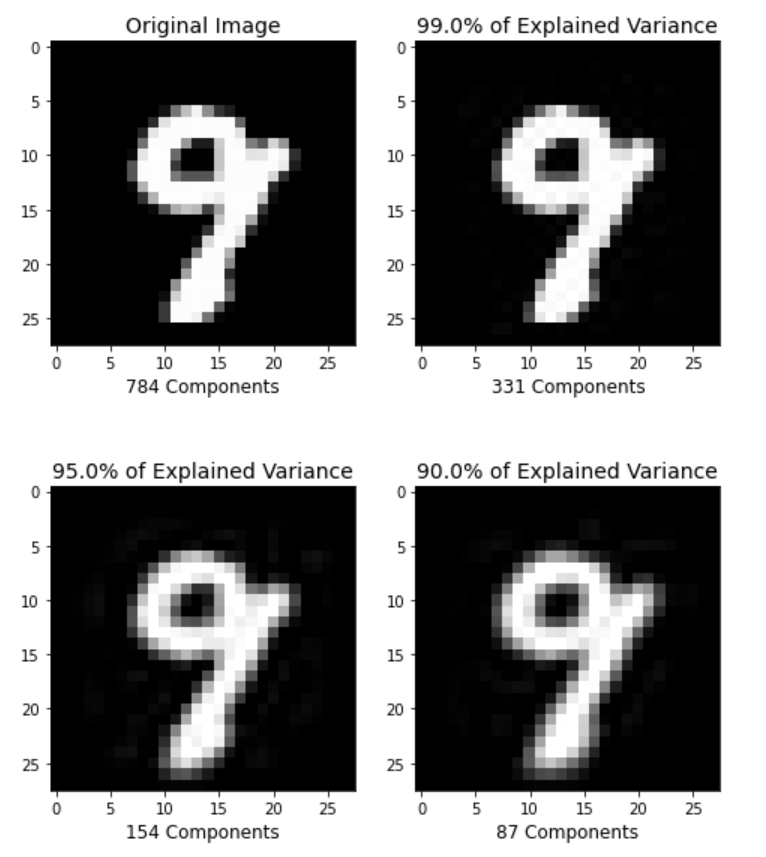
plt.figure(figsize=(8,10));
percentages = [784,0.99,0.95,0.90]
for i in range(1,5):
plt.subplot(2,2,i)
im, n_components = explained_variance(percentages[i-1], X_train)
im = im[5].reshape(28, 28) # 重建成图片
plt.imshow(im,cmap = plt.cm.gray, interpolation='nearest',clim=(0,1))
plt.xlabel(f'{n_components} Components', fontsize = 12)
if i==1:
plt.title('Original Image', fontsize = 14)
else:
plt.title(f'{percentages[i-1]*100}% of Explained Variance', fontsize = 14)
plt.show()