一.简介
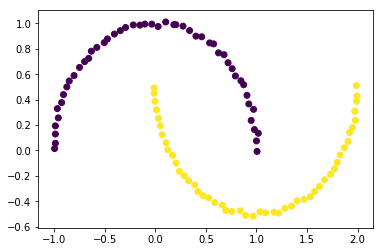
前两节分别实现了硬间隔支持向量机与软间隔支持向量机,它们本质上都是线性分类器,只是软间隔对“异常点”更加宽容,它们对形如如下的螺旋数据都没法进行良好分类,因为没法找到一个直线(超平面)能将其分隔开,必须使用曲线(超曲面)才能将其分隔,而核技巧便是处理这类问题的一种常用手段。
import numpy as np
import matplotlib.pyplot as plt
import copy
import random
import os
os.chdir('../')
from ml_models import utils
from ml_models.svm import *
from sklearn import datasets
%matplotlib inline
data, target = datasets.make_moons(noise=0.01)
plt.scatter(data[:,0],data[:,1],c=target)
plt.show()
二.核技巧
核技巧简单来说分为两步:
(1)将低维非线性可分数据(x),通过一个非线性映射函数(phi),映射到一个新空间(高维度甚至是无限维空间);
(2)对新空间的数据(phi(x))训练线性分类器
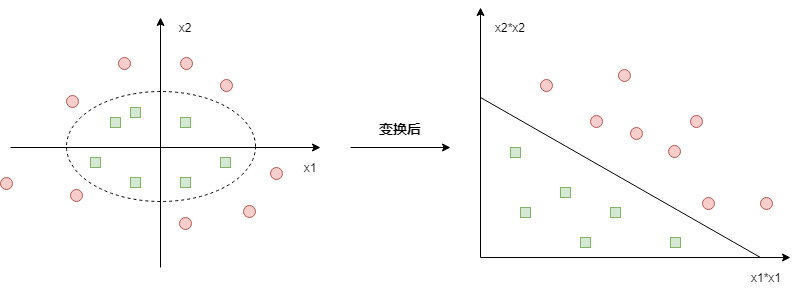
比如如下的情况:
原始数据需要使用一个椭圆才能分隔开,但对原始数据施加一个非线性变换(phi:(x_1,x_2)->(x_1^2,x_2^2))变换后,在新空间中就可以线性分隔了
利用核技巧后的SVM
所以,如果对原始数据施加一个映射,此时软间隔SVM的对偶问题为:
求解得最优(alpha_i^*)后,SVM模型为:
三.核函数
观察一下上面公式,我们的目的其实是求解(phi(x_i)^Tphi(x_j)),有没有一种函数让((x_i,x_j))只在原始空间做计算就达到(phi(x_i)^Tphi(x_j))的效果呢?有的,那就是核函数,即:
怎样的函数才能做核函数?
要成为核函数必须满足如下两点条件:
(1)对称性:(K(x_i,x_j)=K(x_j,x_i))
(2)正定性:对任意的(x_i,i=1,2,..,m),(K(x,z))对应的Gramm矩阵:
是半正定矩阵,这里的(x_iin)可行域,并不要求一定要属于样本集
常见的核函数有哪些?
目前用的比较多的核函数有如下一些:
(1)多项式核函数:
(2)高斯核函数:
显然,线性可分SVM中使用的是(K(x,z)=x^Tz)也是核函数
利用核函数后的SVM
利用核函数后,软间隔SVM的对偶问题为:
求解得最优(alpha_i^*)后,SVM模型为:
四.代码实现
代码实现很简单,就在软间隔SVM的基础上将向量的内积计算(x^Tz)替换为(K(x,z))即可,首先定义一些核函数:
"""
该部分放到ml_model.kernel_functions中
"""
def linear():
"""
线性核函数
:return:linear function
"""
def _linear(x, y):
return np.dot(x, y)
return _linear
def poly(p=2):
"""
多项式核函数
:param p:
:return: poly function
"""
def _poly(x, y):
return np.power(np.dot(x, y) + 1, p)
return _poly
def rbf(sigma=0.1):
"""
径向基/高斯核函数
:param sigma:
:return:
"""
def _rbf(x, y):
np_x = np.asarray(x)
if np_x.ndim <= 1:
return np.exp((-1 * np.dot(x - y, x - y) / (2 * sigma * sigma)))
else:
return np.exp((-1 * np.multiply(x - y, x - y).sum(axis=1) / (2 * sigma * sigma)))
return _rbf
from ml_models import kernel_functions
class SVC(object):
def __init__(self, epochs=100, C=1.0, tol=1e-3, kernel=None, degree=3, gamma=0.1):
"""
:param epochs: 迭代次数上限
:param C: C越小,对于误分类的惩罚越小
:param tol:提前中止训练时的误差值上限,避免迭代太久
:param kernel:核函数
:param degree:kernel='poly'时生效
:param gamma:kernel='rbf'时生效
"""
self.b = None
self.alpha = None
self.E = None
self.epochs = epochs
self.C = C
self.tol = tol
# 定义核函数
if kernel is None:
self.kernel_function = kernel_functions.linear()
elif kernel == 'poly':
self.kernel_function = kernel_functions.poly(degree)
elif kernel == 'rbf':
self.kernel_function = kernel_functions.rbf(gamma)
else:
self.kernel_function = kernel_functions.linear()
# 记录支持向量
self.support_vectors = None
# 记录支持向量的x
self.support_vector_x = []
# 记录支持向量的y
self.support_vector_y = []
# 记录支持向量的alpha
self.support_vector_alpha = []
def f(self, x):
"""
:param x:
:return: wx+b
"""
x_np = np.asarray(x)
if len(self.support_vector_x) == 0:
if x_np.ndim <= 1:
return 0
else:
return np.zeros((x_np.shape[:-1]))
else:
if x_np.ndim <= 1:
wx = 0
else:
wx = np.zeros((x_np.shape[:-1]))
for i in range(0, len(self.support_vector_x)):
wx += self.kernel_function(x, self.support_vector_x[i]) * self.support_vector_alpha[i] *
self.support_vector_y[i]
return wx + self.b
def init_params(self, X, y):
"""
:param X: (n_samples,n_features)
:param y: (n_samples,) y_iin{0,1}
:return:
"""
n_samples, n_features = X.shape
self.b = .0
self.alpha = np.zeros(n_samples)
self.E = np.zeros(n_samples)
# 初始化E
for i in range(0, n_samples):
self.E[i] = self.f(X[i, :]) - y[i]
def _select_j(self, best_i):
"""
选择j
:param best_i:
:return:
"""
valid_j_list = [i for i in range(0, len(self.alpha)) if self.alpha[i] > 0 and i != best_i]
best_j = -1
# 优先选择使得|E_i-E_j|最大的j
if len(valid_j_list) > 0:
max_e = 0
for j in valid_j_list:
current_e = np.abs(self.E[best_i] - self.E[j])
if current_e > max_e:
best_j = j
max_e = current_e
else:
# 随机选择
l = list(range(len(self.alpha)))
seq = l[: best_i] + l[best_i + 1:]
best_j = random.choice(seq)
return best_j
def _meet_kkt(self, x_i, y_i, alpha_i):
"""
判断是否满足KKT条件
:param w:
:param b:
:param x_i:
:param y_i:
:return:
"""
if alpha_i < self.C:
return y_i * self.f(x_i) >= 1 - self.tol
else:
return y_i * self.f(x_i) <= 1 + self.tol
def fit(self, X, y2, show_train_process=False):
"""
:param X:
:param y2:
:param show_train_process: 显示训练过程
:return:
"""
y = copy.deepcopy(y2)
y[y == 0] = -1
# 初始化参数
self.init_params(X, y)
for _ in range(0, self.epochs):
if_all_match_kkt = True
for i in range(0, len(self.alpha)):
x_i = X[i, :]
y_i = y[i]
alpha_i_old = self.alpha[i]
E_i_old = self.E[i]
# 外层循环:选择违反KKT条件的点i
if not self._meet_kkt(x_i, y_i, alpha_i_old):
if_all_match_kkt = False
# 内层循环,选择使|Ei-Ej|最大的点j
best_j = self._select_j(i)
alpha_j_old = self.alpha[best_j]
x_j = X[best_j, :]
y_j = y[best_j]
E_j_old = self.E[best_j]
# 进行更新
# 1.首先获取无裁剪的最优alpha_2
eta = self.kernel_function(x_i, x_i) + self.kernel_function(x_j, x_j) - 2.0 * self.kernel_function(
x_i, x_j)
# 如果x_i和x_j很接近,则跳过
if eta < 1e-3:
continue
alpha_j_unc = alpha_j_old + y_j * (E_i_old - E_j_old) / eta
# 2.裁剪并得到new alpha_2
if y_i == y_j:
L = max(0., alpha_i_old + alpha_j_old - self.C)
H = min(self.C, alpha_i_old + alpha_j_old)
else:
L = max(0, alpha_j_old - alpha_i_old)
H = min(self.C, self.C + alpha_j_old - alpha_i_old)
if alpha_j_unc < L:
alpha_j_new = L
elif alpha_j_unc > H:
alpha_j_new = H
else:
alpha_j_new = alpha_j_unc
# 如果变化不够大则跳过
if np.abs(alpha_j_new - alpha_j_old) < 1e-5:
continue
# 3.得到alpha_1_new
alpha_i_new = alpha_i_old + y_i * y_j * (alpha_j_old - alpha_j_new)
# 5.更新alpha_1,alpha_2
self.alpha[i] = alpha_i_new
self.alpha[best_j] = alpha_j_new
# 6.更新b
b_i_new = y_i - self.f(x_i) + self.b
b_j_new = y_j - self.f(x_j) + self.b
if self.C > alpha_i_new > 0:
self.b = b_i_new
elif self.C > alpha_j_new > 0:
self.b = b_j_new
else:
self.b = (b_i_new + b_j_new) / 2.0
# 7.更新E
for k in range(0, len(self.E)):
self.E[k] = self.f(X[k, :]) - y[k]
# 8.更新支持向量相关的信息
self.support_vectors = np.where(self.alpha > 1e-3)[0]
self.support_vector_x = [X[i, :] for i in self.support_vectors]
self.support_vector_y = [y[i] for i in self.support_vectors]
self.support_vector_alpha = [self.alpha[i] for i in self.support_vectors]
# 显示训练过程
if show_train_process is True:
utils.plot_decision_function(X, y2, self, [i, best_j])
utils.plt.pause(0.1)
utils.plt.clf()
# 如果所有的点都满足KKT条件,则中止
if if_all_match_kkt is True:
break
# 显示最终结果
if show_train_process is True:
utils.plot_decision_function(X, y2, self, self.support_vectors)
utils.plt.show()
def get_params(self):
"""
输出原始的系数
:return: w
"""
return self.w, self.b
def predict_proba(self, x):
"""
:param x:ndarray格式数据: m x n
:return: m x 1
"""
return utils.sigmoid(self.f(x))
def predict(self, x):
"""
:param x:ndarray格式数据: m x n
:return: m x 1
"""
proba = self.predict_proba(x)
return (proba >= 0.5).astype(int)
五.查看效果
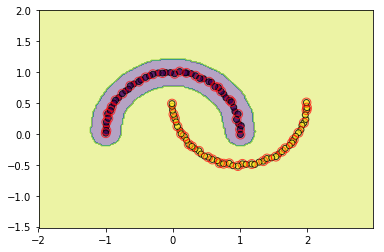
#查看rbf的效果
svm = SVC(C=3.0, kernel='rbf',gamma=0.1, epochs=10, tol=0.2)
svm.fit(data, target)
utils.plot_decision_function(data, target, svm, svm.support_vectors)
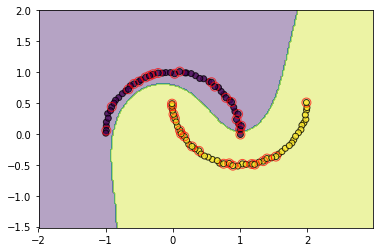
#查看poly的效果
svm = SVC(C=3.0, kernel='poly',degree=3, epochs=10, tol=0.2)
svm.fit(data, target)
utils.plot_decision_function(data, target, svm, svm.support_vectors)
六.问题讨论
1.RBF函数中(sigma)的不同取值对训练的影响
为了探索该问题,我们对(sigma)从小到大取一组数,在另外一个伪数据上查看效果
from sklearn.datasets import make_classification
data, target = make_classification(n_samples=100, n_features=2, n_classes=2, n_informative=1, n_redundant=0,
n_repeated=0, n_clusters_per_class=1, class_sep=.5,random_state=21)
c1 = SVC(C=3.0, kernel='rbf',gamma=0.1, epochs=10, tol=0.01)
c1.fit(data, target)
c2 = SVC(C=3.0, kernel='rbf',gamma=0.5, epochs=10, tol=0.01)
c2.fit(data, target)
c3 = SVC(C=3.0, kernel='rbf',gamma=2, epochs=10, tol=0.01)
c3.fit(data, target)
plt.figure(figsize=(16,4))
plt.subplot(1,3,1)
utils.plot_decision_function(data,target,c1)
plt.subplot(1,3,2)
utils.plot_decision_function(data,target,c2)
plt.subplot(1,3,3)
utils.plot_decision_function(data,target,c3)
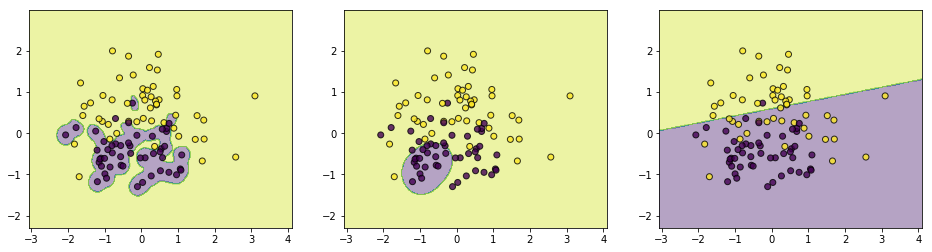
上面(sigma)分别取值([0.1,0.5,2]),通过结果可以简单总结如下:
(1)如果(sigma)取值越小,SVM越能抓住个别样本的信息,越容易过拟合;
(2)(sigma)取值越大SVM的泛化能力越强
如何对该结果进行理解呢?可以通过样本点在映射空间的距离来看,对任意两个样本点(x,z),它们在映射空间中的距离的平方可以表示如下:
所以:
(1)如果(sigma ightarrow 0),那么(-frac{midmid x-zmidmid^2}{2sigma^2} ightarrow -infty),那么(exp(-frac{midmid x-zmidmid^2}{2sigma^2}) ightarrow 0),那么(||phi(x)-phi(z)|| ightarrow sqrt 2)
(2)如果(sigma ightarrow infty),那么(-frac{midmid x-zmidmid^2}{2sigma^2} ightarrow 0),那么(exp(-frac{midmid x-zmidmid^2}{2sigma^2}) ightarrow 1),那么(||phi(x)-phi(z)|| ightarrow 0)
我们可以验证上面的总结,若(sigma)取值越小,样本点在映射空间越分散,则在高维空间越容易线性可分,表现在低维空间则越容易过拟合;(sigma)取值越大,样本点在映射空间越集中,越不易线性可分,表现在低维空间也是不易线性可分
2.如何理解RBF可将数据映射到无限维空间
原谅自己,这部分公式不想码了,具体内容参考大神的知乎帖子>>>,其中主要需要用到两个等式变换:
(1)指数函数的泰勒级数:(e^x=sum_{n=1}^{infty}frac{x^n}{n!}),将RBF函数进行展开;
(2)利用多项式展开定理,将样本(x)与(z)在原始空间的内积的(n)次方进行展开,假如(x,zin R^k),那么:
这里,(sum_{i=1}^kn_{l_i}=n),(L=frac{(n+k-1)!}{n!(k-1)!}),进一步的,上面等式可以化简为形如这样的表达式:(Phi(x)^TPhi(z)),(Phi(x)=[Phi_1(x),Phi_2(x),cdots ,Phi_L(x)])