突然安利的网站:Usaco;
1.Chocolate Buying

首先看B<=10^18,显然B很大了,因此如果我们写了一个复杂度带B的算法,显然会炸,一般复杂度在1e8左右可以跑过,因此我们要设计一个时间复杂度不带B的算法;
SOLUTION:
把巧克力按价格从小到大排,然后分两种情况:1.剩余的钱可以使所有喜欢这种巧克力的牛都开心;2.没有足够余钱使喜欢这种巧克力的牛全都开心,只能使一部分开心;
严谨证明:
其实很好理解,花同样的钱,如果可以使更多的牛开心,我们显然选择花更少的钱使更多的牛开心;
贪心的三种证法:
- 反证
- 直觉
- 替换
2.Creative Accounting

(使得:Σ ai(i:l~r))
看到求区间和问题,应该条件反射前缀和;
然后我们将题目求原数组区间和最大转化为求原数组的前缀和差最大;
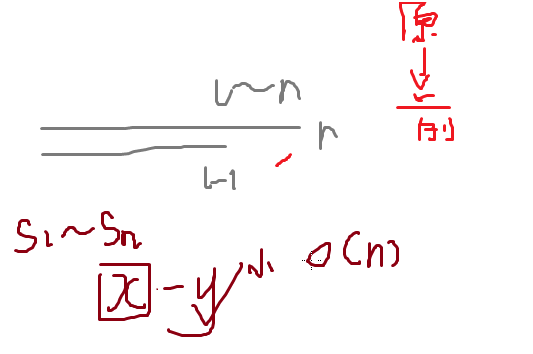
然后我们假设模M后差最大的两个前缀和为x和y;
我们枚举x从s1~sn,然后对于y,有两种情况:(应该是要保证y在x前面)
1.x>=y,此时(x-y) mod M的值就为x-y所得结果再模M;因此最大值可能是x-y,那么找最小的y,这样可以使得x-y的值最大;
2.y>x,此时(x-y) mod M的值是x+M-y的结果再模M;所以我们要使结果最大,就要找到大于x的且最接近x的y;
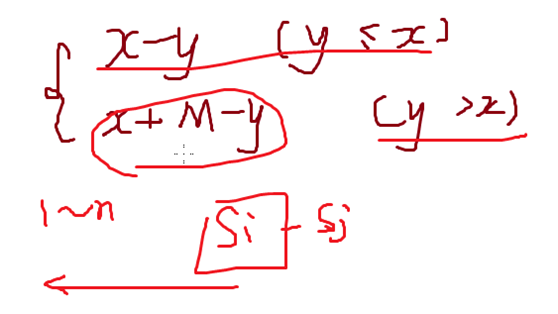
突然插画:
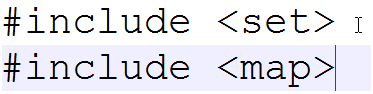
比较重要的qwq↑
好,都不会用。
3.会场安排
【连接】http://ybt.ssoier.cn:8088/problem_show.php?pid=1422

然后之前是做过的,贪心的按照右端点从小到大排序,遍历每一个区间,如果没有重叠就选择这个活动;
这是我们的做法↑
然后这个是lyd的思路:


要注意,楼上↑的for循环枚举的是时间;
4.喷水装置:
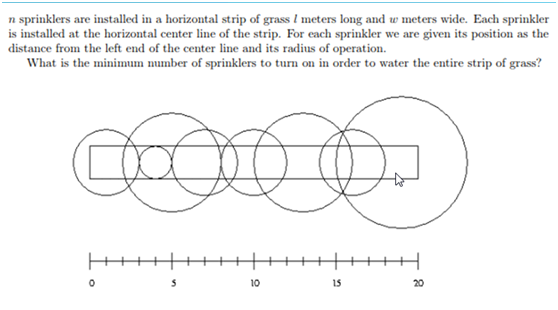
突然安利教辅:
刘汝佳:算法竞赛入门经典训练指南(紫)算法
算法竞赛入门经典训练指南(蓝)刷题
黑书qwq;
算法导论nice~;
对于一个圆来说,真正有用的部分:
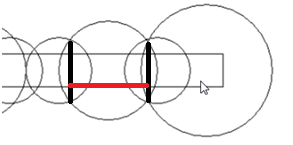
所以我们就可以转化成线段覆盖问题啦;
处理每个圆代表一段线段;
求最小的线段条数,使之完全覆盖;
流程:读入=>处理成线段=>线段覆盖=>输出;
写程序=>结构化;


5.
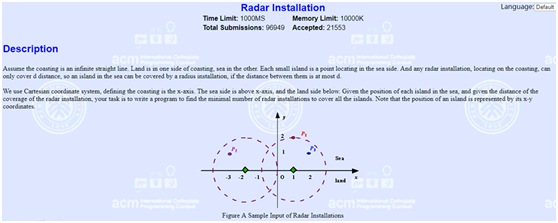
SOLUTION:
以岛屿为 处理突破点,然后以d(给出的雷达半径)为半径,以岛屿为圆心画圆,找到与x轴两个交点,这样每个岛屿对应一条线段;
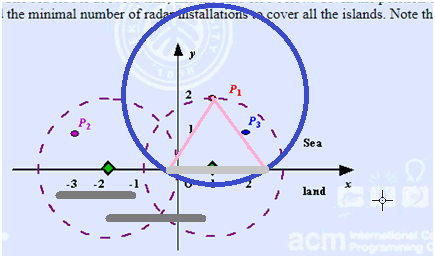
转化为点覆盖线段问题;
然后将所有线段按照区间右端点从小到大排序,如果区间右端点相同的,按照区间左端点从大到小排,然后定义一个nowend,表示当前最右的一个点放在了哪里,如果当前区间的左端点比nowend小(说明nowend也被覆盖在当前区间),continue;否则的伐我们在当前区间的最右放一个雷达,nowend=ennd[i],答案+1;

#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<cstring> #define ll long long using namespace std; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch>'9'||ch<'0') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int n=1,d=1; int x[1010],y[1010],num[1010]; double str[1010],ennd[1010],zz; double dist(double y){ double z=zz-y*y; if(z<0) return -1; double ans=sqrt(z); return ans; } bool cmp(int a,int b){ if(ennd[a]==ennd[b]) return str[a]>str[b]; return ennd[a]<ennd[b]; } void solve(){ sort(num+1,num+n+1,cmp); double nowend=ennd[num[1]]; int ans=1; for(int i=2;i<=n;i++){ if(nowend>=str[num[i]]) continue; else { nowend=ennd[num[i]]; ans++; } } printf("%d ",ans); } int main() { int cnt=0; while(n!=0&&d!=0){ n=read();d=read(); if(n==0&&d==0) break; cnt++; memset(x,0,sizeof(x));memset(y,0,sizeof(y)); memset(str,0,sizeof(str));memset(ennd,0,sizeof(ennd)); memset(num,0,sizeof(num)); zz=(double)d*(double)d; double z;bool bj=0; if(d<0) bj=1; for(int i=1;i<=n;i++){ x[i]=read();y[i]=read(); z=dist((double)y[i]); if(z==-1) bj=1; str[i]=(double)x[i]-z; ennd[i]=(double)x[i]+z; num[i]=i; } printf("Case %d: ",cnt); if(bj) printf("-1 "); else solve(); } return 0; }
6.

贪心的想,显然我们应该先把杀完以后可以使血量增加的杀掉,这样可以积累更多的血,以备后面那些杀完之后使血量减少的怪物用。
因此我们可以分成两个部分,分别记录杀完以后血量增加的,和杀完以后血量减少的。
对于使血量增加的部分,很容易想我们应该先杀伤害小的(如果啥伤害大的可能出现gameover但实际还有更有解的可能[en……感性理解一下]),所以对于使血量增加的部分,我们按照伤害d从小到大排序。
对于使血量减少的部分,我们按照回血量a从大到小排序:因为显然剩下的不管杀哪一个,血量都会在之前的血量下减少,因此我们尽量让回血多一些;
然后按照以上思路排序之后,直接模拟即可;
如果半路出现血量<=0了,直接输出NIE,return 0;
然后一定要记得将当前血量z开long long

#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<cstring> #define ll long long using namespace std; inline int read(){ int ans=0; char last=' ',ch=getchar(); while(ch>'9'||ch<'0') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int n,x,y,upc,downc; ll z; struct node{ int a,d,id; }up[100005],down[100005]; bool cmp1(node i,node j){ return i.d<j.d; } bool cmp2(node i,node j){ return i.a>j.a; } int main(){ n=read();scanf("%lld",&z); for(int i=1;i<=n;i++){ x=read();y=read(); if(x>y) down[++downc].a=y,down[downc].d=x,down[downc].id=i; else up[++upc].a=y,up[upc].d=x,up[upc].id=i; } sort(up+1,up+upc+1,cmp1); sort(down+1,down+downc+1,cmp2); for(int i=1;i<=upc;i++){ z-=up[i].d; if(z<=0){ printf("NIE"); return 0; } z+=up[i].a; } for(int i=1;i<=downc;i++){ z-=down[i].d; if(z<=0) { printf("NIE"); return 0; } z+=down[i].a; } printf("TAK "); for(int i=1;i<=upc;i++)printf("%d ",up[i].id); for(int i=1;i<=downc;i++) printf("%d ",down[i].id); return 0; }


7.

很好想的思路,首先打表1~k的阶乘(数据量应该很小的qwq)
然后我们从最大的阶乘减过来,如果最后可以减为0,就是某个数的阶乘,否则不是;
8.

两种思路:
- 可以把最大的提到最前:
把最大的往前提,然后再把次大的往前提;
2.不能把最大值提到最前面
把前k个中最大的往前提
9.过河问题:

输入输出样例:

首先解释样例:
1~2过河,1送回来;
5~10过河,2送回来;
1~2过河;
直觉:最慢两人要搭伙过河;
设AB为最快的,CD为最慢的
把CD送过河的两种方案:

取楼上两种方法的最小值;
将CD送过河之后,变成子问题;人数每次减2;
减到最后,有两种情况:
1.四个人,直接在进行楼上的操作;
2.三个人,A来回送叭:


神仙k搜索:
贪心的搜索:将搜索树最优的放在最左边,越右越不优,然后允许搜次优解。K=x表示可以搜几个次优解qwq(注意是用k减去楼下边的权)
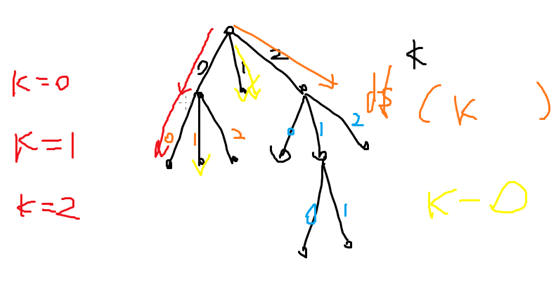
模拟退火;???
看到比它强的就走,比它弱的有一定概率往那走;