【洛谷p1983】车站分级

日常题前废话：

真的感觉估计图论题的边数是个unbelievable的玄学操作啊qwq

然后去翻白书：一个n阶的完全无向图含有n*（n-1）/2条边，一个n阶的完全有向图含有n*(n-1)条边。（这里阶好像是点数？？？）

就是因为没估计好边数，然后wa了好几次emmm

然后这道题用到拓扑排序，因此然后所以

你看这个博客它又大又圆，感觉好多东西都明日复明日，明日何其多了。

---

首先这道题是已知线路，让求最小分级数，咱也不知道为啥就用拓扑排序解了，反正就是用拓扑排序做就对啦。

然后首先是建图连边，这里我们的连边是在起点到终点之前所有的点中，从没停的点向停了的点连一条边，然后要注意不要连重边减小时间复杂度（然后还要注意的是连边是讲起点与终点之间的车站进行连边，并不是所有的都连边）。

样例第一条线路连边

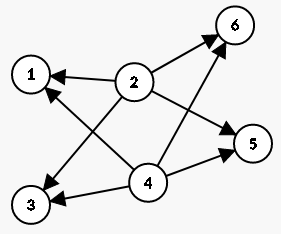
样例第二条线路连边：

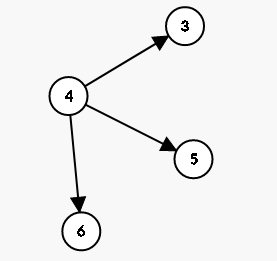
这整个样例的图（我猜会非常拥挤然后没有然后）

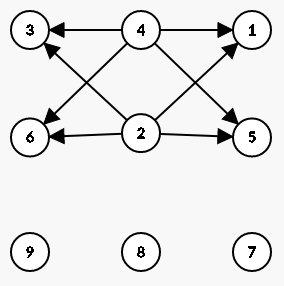
首先扫描所有入度为0的点，将他们的级别设成1，加入队列。

然后进行while的（应该是bfs）{

• 首先将对顶元素出队，删去这个点所有的出边；
• 被删去边的终点入度--；
• 如果删去这条边后被删去边的终点的入度为0，就将其加入队列，然后它的级别定义为现在搜索的点+1（具体因为队列是有序加入的，因此一定最后加入的是级别最高的）

}  

• 最后扫描所有级别，输出最大的就好啦；

CODE：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<string>
#include<queue>

using namespace std;

int n,m,head[2010],cnt,a[2010][2010],vis[2010],t[2010],du[2010],jb[2010][2010];
struct node{
    int to,next;
}edge[2010000];

void add(int from,int to){
    edge[++cnt].to=to;
    edge[cnt].next=head[from];
    head[from]=cnt;
}

queue<int> q;

int main(){
    scanf("%d %d",&n,&m);
    for(int i=1;i<=m;i++){
        scanf("%d",&a[i][0]);
        memset(vis,0,sizeof(vis));
        for(int j=1;j<=a[i][0];j++)
            scanf("%d",&a[i][j]),vis[a[i][j]]=1;
        for(int j=a[i][1];j<=a[i][a[i][0]];j++){
            if(!vis[j]){
                for(int k=1;k<=a[i][0];k++){
                  if(!jb[j][a[i][k]]){
                      add(j,a[i][k]);
                      jb[j][a[i][k]]=1;
                      du[a[i][k]]++;
                   }
                }
            } 
        }
    }
    for(int i=1;i<=n;i++){
        if(!du[i]){
            q.push(i);t[i]=1;
        } 
    }
    while(!q.empty()){
        int d=q.front();
        q.pop();
        for(int i=head[d];i;i=edge[i].next){
            du[edge[i].to]--;
            if(!du[edge[i].to]){
                t[edge[i].to]=t[d]+1;
                q.push(edge[i].to);
            }
        }  
    }
    sort(t+1,t+n+1);
    cout<<t[n]<<endl;
}

end-