自已做动画及编写程序搞清楚最大堆的实现原理

目录

• 背景
• 概念
• 最大堆
  • 最大堆的线性存储
  • 动画实现最大堆加入新元素
  • 代码实现最大堆加入新元素
  • 动画实现最大堆取出最大元素
  • 代码实现最大堆取出最大元素
  • 程序测试
• 最大堆的应用--优先队列
• 写在最后

背景

• 二叉树是数据结构中的重点，也是难点。二叉树比数组、栈、队列等线性结构相比复杂度更高，想要做到心中有“树”，需要自己动手画图、观察、思考，才能领会其真谛。
• 在上篇文章《自己动手作图深入理解二叉树、满二叉树及完全二叉树》中，我们对完全二叉树有了一定认识，该文将对一种特殊的完全二叉树”最大堆”进行底层研究。

概念

堆（heap)通常是一个可以被看做一棵二叉树的数组对象。堆总是满足下列性质：

• 堆总是一棵完全二叉树。
• 堆中某个节点的值总是不大于或不小于其父节点的值；

最大堆

• 根节点最大的堆叫做最大堆
  

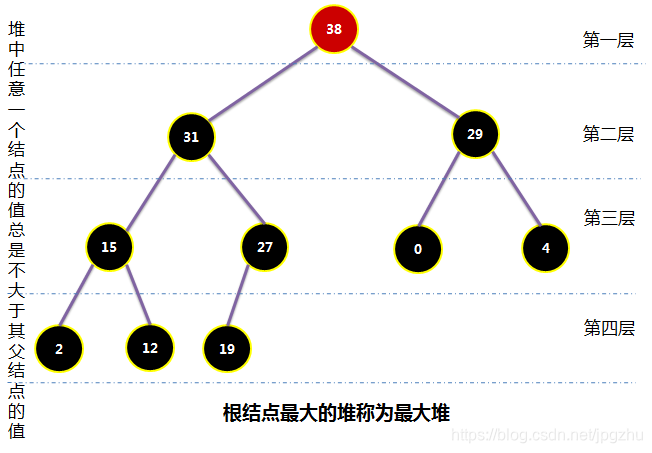
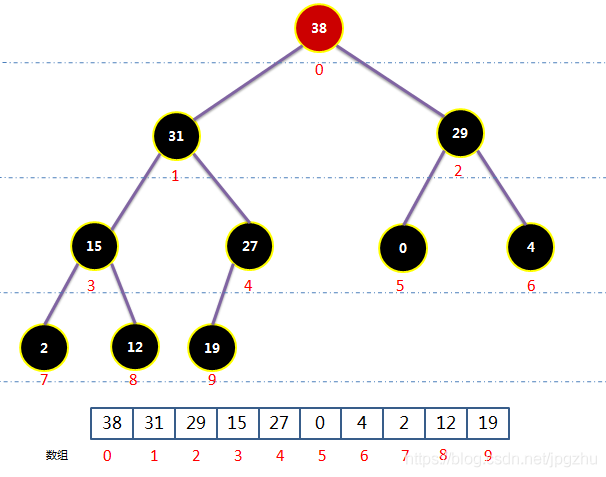
最大堆的线性存储

• 由于堆是一种特殊的完全二叉树，可以利用数组集合形成线性存储的数据结构。
  

/**
 * 最大堆的底层实现--数组集合形成线性存储的数据结构
 *  * @author zhuhuix
 * @date 2020-06-28
 */
public class MaxHeap<E extends Comparable<E>> {

    // 存放元素的数组集合
    private ArrayList<E> list;

    MaxHeap() {
        this.list = new ArrayList<>();
    }

    // 得到左孩子索引
    private int getLeftChildIndex(int i) {
        return (2 * i + 1);
    }

    // 得到右孩子索引
    private int getRightChildIndex(int i) {
        return (2 * i + 2);
    }

    // 得到父结点索引
    private int getParentIndex(int i) {
        if (i == 0) {
            throw new IllegalArgumentException("非法索引值");
        } else {
            return ((i - 1) / 2);
        }
    }
}

动画实现最大堆加入新元素

• 加入到数组集合尾部的元素与父结点进行比较，通过上浮操作，保证所有子结点不能大于父结点。
  

代码实现最大堆加入新元素

/**
 * 最大堆的底层实现
 *
 * @author zhuhuix
 * @date 2020-06-28
 */
public class MaxHeap<E extends Comparable<E>> {

    // 存放元素的数组集合
    private ArrayList<E> list;

    MaxHeap() {
        this.list = new ArrayList<>();
    }

    // 得到左孩子索引
    private int getLeftChildIndex(int i) {
        return (2 * i + 1);
    }

    // 得到右孩子索引
    private int getRightChildIndex(int i) {
        return (2 * i + 2);
    }

    // 得到父结点索引
    private int getParentIndex(int i) {
        if (i == 0) {
            throw new IllegalArgumentException("非法索引值");
        } else {
            return ((i - 1) / 2);
        }
    }

    // 添加元素
    public void add(E e) {
        this.list.add(e);
        /**
         * 将加入的结点与父结点进行比较：
         * 如果加入的结点大于父结点，则进行上浮
         * 直至新结点小于或等于父结点为止
         */

        // 获取当前添加元素在数组中的索引
        int i = this.list.size() - 1;
        while (i > 0) {
            E current = this.list.get(i);
            E parent = this.list.get(getParentIndex(i));
            // 如果父结点元素大于当前加入的元素，则进行交换
            if (parent.compareTo(current) < 0) {
                // 交换新加入的结点与父结点的位置
                Collections.swap(this.list, i, getParentIndex(i));
            } else {
                break;
            }
            i = getParentIndex(i);
        }
    }
    
}

动画实现最大堆取出最大元素

• 获取最大堆中的根结点，即为最大元素；并把尾部结点放置到根结点，并通过下沉操作，把子结点中的最大元素移动根结点。
  

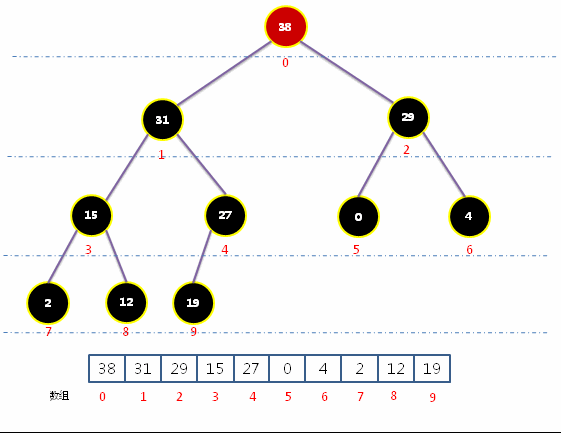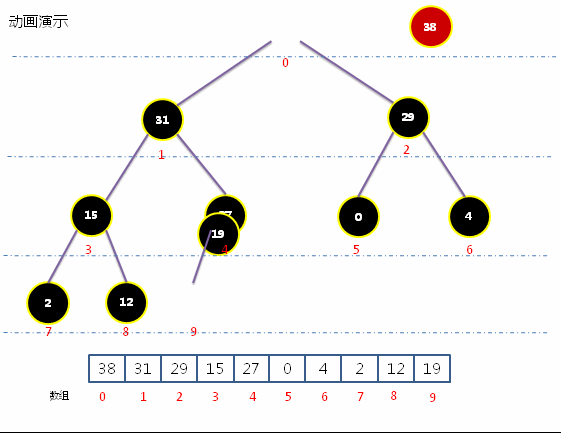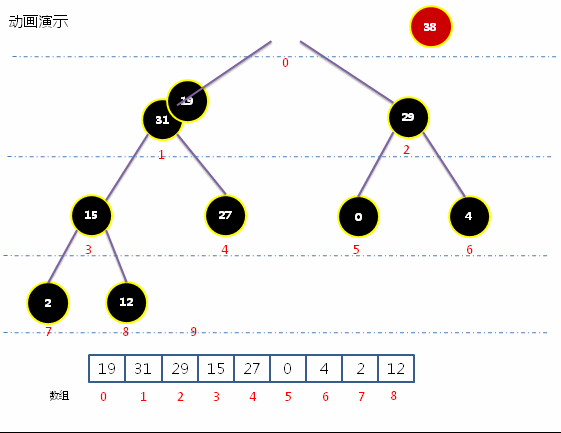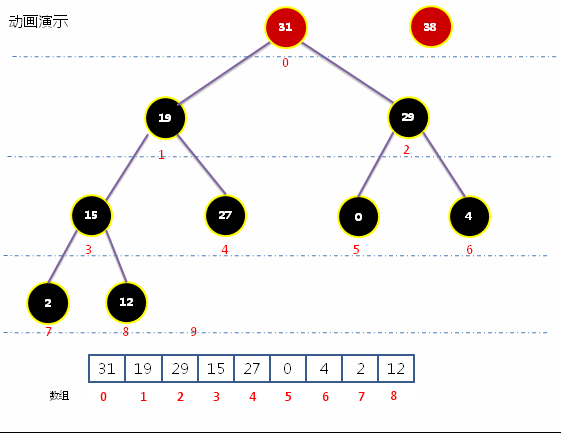
代码实现最大堆取出最大元素

/**
 * 最大堆的底层实现
 *
 * @author zhuhuix
 * @date 2020-06-28
 */
public class MaxHeap<E extends Comparable<E>> {

    // 存放元素的数组集合
    private ArrayList<E> list;

    MaxHeap() {
        this.list = new ArrayList<>();
    }

    // 得到左孩子索引
    private int getLeftChildIndex(int i) {
        return (2 * i + 1);
    }

    // 得到右孩子索引
    private int getRightChildIndex(int i) {
        return (2 * i + 2);
    }

    // 得到父结点索引
    private int getParentIndex(int i) {
        if (i == 0) {
            throw new IllegalArgumentException("非法索引值");
        } else {
            return ((i - 1) / 2);
        }
    }

    // 查找最大元素
    public E findMax() {
        if (this.list.size() == 0) {
            return null;
        }
        // 最大堆中的元素永远在根结点
        return this.list.get(0);
    }

    // 取出最大元素
    public E getMax() {
        if (findMax() != null) {
            E e = findMax();

            /**
             * 取出最大元素后，需要把堆中第二大的元素放置在根结点：
             * 将根结点元素与最后面的元素进行交换，
             * 让最后面的元素出现在根结点，并移除最大元素
             * 将根结点的元素与左右孩子结点比较，直至根结点的元素变成最大值
             */
            int i = 0;
            Collections.swap(this.list, i, this.list.size() - 1);
            this.list.remove(this.list.size() - 1);

            // 通过循环进行当前结点与左右孩子结点的大小比较
            while (getLeftChildIndex(i) < this.list.size() && getRightChildIndex(i) < this.list.size()) {
                int leftIndex = getLeftChildIndex(i);
                int rightIndex = getRightChildIndex(i);

                // 通过比较左右孩子的元素哪个较大，确定当前结点与哪个孩子进行交换
                int index = this.list.get(leftIndex).compareTo(this.list.get(rightIndex)) > 0 ? leftIndex : rightIndex;
                if (this.list.get(i).compareTo(this.list.get(index)) < 0) {
                    Collections.swap(this.list, i, index);
                } else {
                    // 如果当前结点都大于左右孩子，则结束比较
                    break;
                }
                i = index;
            }

            return e;
        } else {
            return null;
        }
    }
}

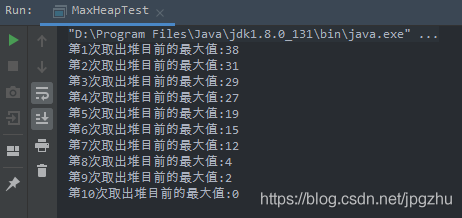
程序测试

/**
 * 最大堆的底层实现--测试程序
 *
 * @author zhuhuix
 * @date 2020-06-28
 */
public class MaxHeapTest {
    public static void main(String[] args) {
        MaxHeap<Integer> maxHeap = new MaxHeap<>();

        // 将10个数字加入形成最大堆
        int[] arrays = {19,29,4,2,27,0,38,15,12,31};
        for (int i = 0; i < arrays.length; i++) {
            maxHeap.add(arrays[i]);
        }

        // 依次从堆中取出最大值
        for (int i = 0; i < arrays.length; i++) {
            System.out.println("第"+(i+1)+"次取出堆目前的最大值:"+maxHeap.getMax());
        }
    }
}

最大堆的应用--优先队列

优先队列:出队的和顺序与入队的顺序无关,只与优先级相关；
优先队列通常可以采用最大堆的数据结构来实现。

/**
 * 用最大堆的数据结构实现优先队列
 * 
 * @author zhuhuix
 * @date 2020-06-28
 */
public class PriorityQueue<E extends Comparable<E>>  {
    private MaxHeap<E> mhp;
    PriorityQueue() {
        mhp=new MaxHeap<>();
    }

    // 入队
    public void enqueue(E e) {
        mhp.add(e);
    }

    // 优选级最高的元素出队
    public E dequeue() {
        return mhp.getMax();
    }

    // 查看优先级最高的元素
    public E getFront() {
        return mhp.findMax();
    }
}

写在最后

• 以上通过画图、动画演示、代码编写对堆与最大堆的概念和底层实现方式，都作了深入分析；作为最大堆的反向结构，最小堆的实现也是一样，读者可参考以上动画和代码，动手练习。
• 画图、编码不易，请点赞、收藏、关注三连！！！