罚函数之乘子法

外罚函数主要用于对于等式约束问题的求解，内点法主要是对于不等式问题的求解，一般问题中包含等式约束以及不等式约束，故需要使用乘子法解决问题。

1、 乘子法概述

（1）等式约束乘子法描述：

min f(x) 

s.t. g_i(x) =0

广义乘子法是拉格朗日乘子法与罚函数法的结合，构造增广函数：

φ (x,λ,σ)=f(x)+λ^Tg(x)+1/2σg^T(x)g(x)

在罚函数的基础上增加了乘子项，首先在σ足够大的基础上，获得ϕ的极小值，然后在调整λ获得原问题的最优解。

（2）包含等式约束以及不等式约束问题描述：

min f(x) 

        s.t. h_i(x) =0,i=1,...,l  

               g_i(x)≥0,i=1,...m

其基本思想是：先引进辅助变量把不等式约束化为等式约束，然后利用最优性条件消去辅助变量，主要是通过构造增广拉格朗日函数，进行外迭代与内迭代综合，带入乘子迭代公式，进而得出得出，故针对上述一般问题构造拉格朗日函数为：

4、其代码实现为

function [x,mu,lambda,output]=multphr(fun,hf,gf,dfun,dhf,dgf,x0)

%功能：用乘子法解一般约束问题：min f(x),s.t. h(x)=0.g(x)>=0

%输入：x0是初始点，fun，dfun分别是目标函数及其梯度；

%hf，dhf分别是等式约束（向量）函数及其jacobi矩阵的转置；

%gf，dgf分别是不等式约束（向量）函数及其jacobi矩阵的转置；

%输出：x是近似最优点，mu，lambda分别是相应于等式约束和不等式

%     等式约束的乘子向量；output是结构变量，输出近似极小值f，迭代次数，内迭代次数等

%%%%%%c初始化相关参数%%%%%%%%%%%

maxk=500;       %最大迭代次数

sigma=2.0;      %罚因子

eta=2.0;    theta=0.8;  %PHR算法中的实参数

k=0; ink=0;  %k,ink分别是外迭代和内迭代次数

epsilon=1e-5;%终止误差值

x=x0;he=feval(hf,x);gi=feval(gf,x);%he=feval(hf,x)=hf(x)

n=length(x);l=length(he);m=length(gi);

%选取乘子向量的初始值

mu=0.1*ones(1,1);lambda=0.1*ones(m,1);%ones为生成m*n的全1矩阵

btak=10;    btaold=10;  %用来检验终止条件的两个值

while (btak>epsilon & k<maxk)

    %%%%%%c先求解无约束问题%%%%%%%%%%%

    %调用BFGS算法程序求解无约束子问题

    [x,v,ik]=bfgs('mpsi','dmpsi',x0,fun,hf,gf,dfun,dhf,dgf,mu,lambda,sigma);%%其中x为最优点，val为最优值，ik为迭代次数

    ink=ink+ik;

    he=feval(hf,x);gi=feval(gf,x);

    %%%%%%%%%%计算btak%%%%%%%%%%%

    btak=0.0;

    for(i=1:l),btak=btak+he(i)^2;   end

    for(i=1:m)

        temp=min(gi(i),lambda(i)/sigma);

        btak=btak+temp^2;

    end

    btak=sqrt(btak);

    if btak>epsilon

        %%%%%%%%%%%更新罚参数%%%%%%%%%%%

        if(k>=2 & btak>theta*btaold)

            sigma=eta*sigma;

        end

        %%%%%%%%%%%更新乘子向量%%%%%%%%%%%%

        for(i=1:l),mu(i)=mu(i)-sigma*he(i);end

        for(i=1:m)

            %lambda(i)=max(0.0,lambda(i)-sigma*gi(i));

lambda(i)=max(0.0,lambda(i)-gi(i));

        end

    end

     %%%%%%%%%%%迭代%%%%%%%%%%%%

    k=k+1;

    btaold=btak;

    x0=x;

end

f=feval(fun,x);

output.fval=f;

output.iter=k;

output.inner_iter=ink;

output.bta=btak;

BFGS算法部分：

function [x,val,k]=bfgs(fun,gfun,x0,varargin)

%功能：用BFGS算法求解无约束问题：minf（x）

%输入：x0是初始点，fun，gfun分别是目标函数及其梯度

%varargin是输入的可变参数变量，简单调用bfgs时可以忽略，其他程序调用则尤为重要

%输出：x为最优点，val为最优值，k时迭代次数

maxk=500;%给出最大迭代次数

rho=0.55;sigma=0.4;epsilon=1e-5;

k=0;n=length(x0);

Bk=eye(n);%Bk=feval('Hess',x0)

while(k<maxk)

    gk=feval(gfun,x0,varargin{:});%计算梯度

    if(norm(gk)<epsilon),break;end%检验终止准则

    dk=-Bkgk;%解方程组，计算搜索方向

    m=0;mk=0;

    while(m<20)%搜索求步长

        newf=feval(fun,x0+rho^m*dk,varargin{:});

        oldf=feval(fun,x0,varargin{:});

        if(newf<oldf+sigma*rho^m*gk'*dk)

            mk=m;break;

        end

        m=m+1;

    end

       %bfgs校正

    x=x0+rho^mk*dk;

    sk=x-x0;yk=feval(gfun,x,varargin{:})-gk;

    if(yk'*sk>0)

        Bk=Bk-(Bk*sk*sk'*Bk)/(sk'*Bk*sk)+(yk*yk')/(yk'*sk);

    end

    k=k+1;x0=x;

end

val=feval(fun,x0,varargin{:});

主函数部分为：

%目标函数文件

function f=f1(x)

f=(x(1)-2.0)^2+(x(2)-1.0)^2;

%等式约束条件

function he=h1(x)

he=x(1)-2.0*x(2)+1.0;

%不等式约束条件

function gi=g1(x)

gi=-0.25*x(1)^2-x(2)^2+1;

%目标函数的梯度文件

function g=df1(x)

g=[2.0*(x(1)-2.0),2.0*(x(2)-1.0)]';

%等式函数的Jacobi（转置）矩阵文件

function dhe=dh1(x)

dhe=[1.0,-2.0]';

%不等式约束函数的Jacobi矩阵（转置矩阵）

function dgi=dg1(x)

dgi=[-0.5*x(1),-2.0*x(2)]';

命令行指令为：

x0=[3,3]'

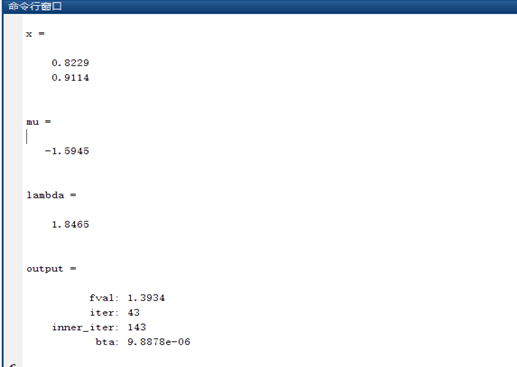
[x,mu,lambda,output]=multphr('f1','h1','g1','df1','dh1','dg1',x0)

输出结果如下：