Tarjan算法求图的割点和桥-模版

2020-09-26 15:51:22

一、定义

割点：无向连通图中，某点和其连接的边去除后，图不再连通

桥：无向连通图中，某边去除后，图不再连通

二、Tarjan算法

Tarjan算法可以在一次dfs中得到所有的割点和割边。

time: 时间戳

dfn[]: dfs第一次遍历到的时间戳

low[]: 通过子节点能够访问到的最小时间戳

fa[]: 记录父亲节点

• 割点

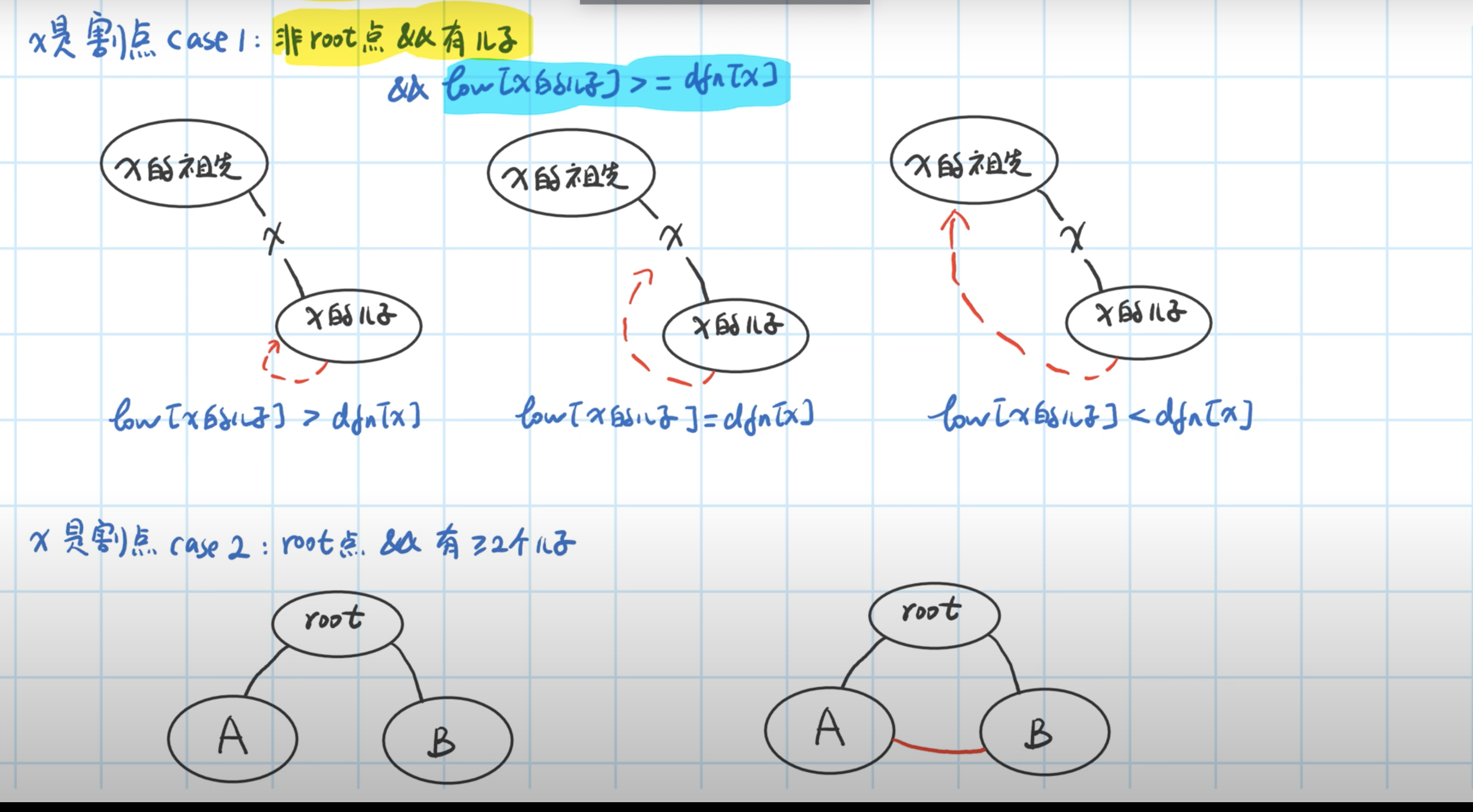
• 桥

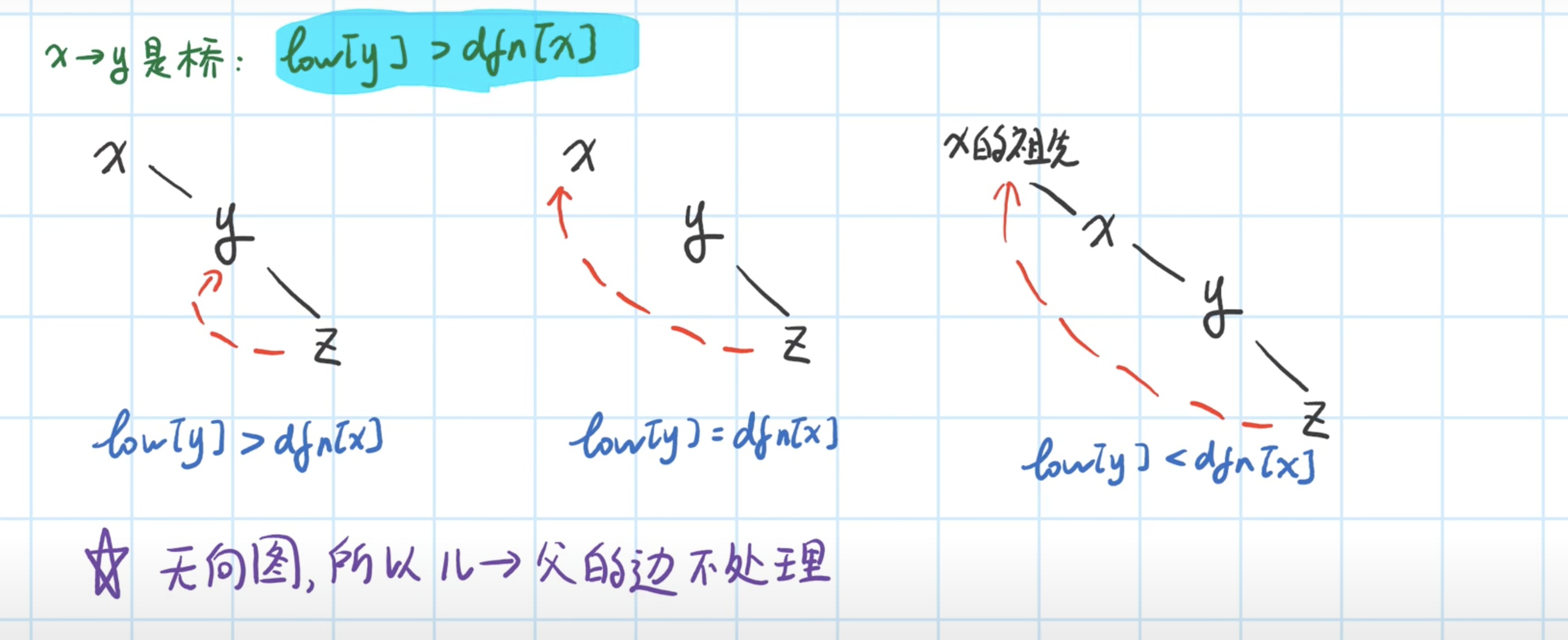
• 总结

三、模版

LC. 1568

    int time = 1;
    int[] dfn = new int[1000];
    int[] low = new int[1000];
    int[] fa = new int[1000];
    Set<Integer> set = new HashSet<>();
    int bridge = 0;
    int[][] dirs = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};
    
    int m;
    int n;
    
    
    public int minDays(int[][] grid) {
        Arrays.fill(fa, -1);
        m = grid.length;
        n = grid[0].length;
        int cnt = 0;
        int total = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 0) continue;
                total += 1;
                int node = i * n + j;
                if (dfn[node] == 0) {
                    dfs(grid, i, j);
                    cnt += 1;
                }
            }
        }
        if (cnt == 0 || cnt > 1) return 0;
        if (set.size() > 0 || total == 1) return 1;
        else return 2;
    }
    
    private void dfs(int[][] grid, int i, int j) {
        int node = i * n + j;
        dfn[node] = time;
        low[node] = time;
        time += 1;
        int child = 0;
        for (int[] dir : dirs) {
            int ni = i + dir[0];
            int nj = j + dir[1];
            if (ni < 0 || ni >= m || nj < 0 || nj >= n) continue;
            if (grid[ni][nj] == 1) {
                int next = ni * n + nj;
                if (dfn[next] == 0) {
                    child += 1;
                    fa[next] = node;
                    dfs(grid, ni, nj);
                    if (fa[node] == -1 && child >= 2) {
                        set.add(node);
                    }
                    if (fa[node] != -1 && low[next] >= dfn[node]) {
                        set.add(node);
                    }
                    if (low[next] > dfn[node]) {
                        bridge += 1;
                    }
                    low[node] = Math.min(low[node], low[next]);
                }
                else if (next != fa[node]) {
                    low[node] = Math.min(low[node], low[next]);
                }
            }
        }
    }