• 算法导论-顺序统计-快速求第i小的元素

    目录                                                              

    1、问题的引出-求第i个顺序统计量

    2、方法一：以期望线性时间做选择

    3、方法二（改进）：最坏情况线性时间的选择

    4、完整测试代码（c++）

    5、参考资料

    内容                                                               

    1、问题的引出-求第i个顺序统计量                                        

       什么是顺序统计量？及中位数概念

       在一个由元素组成的集合里，第i个顺序统计量（order statistic）是该集合第i小的元素。例如，最小值是第1个顺序统计量(i=1)，最大值是第n个顺序统计量(i=n)。一个中位数（median）是它所在集合的“中点元素”。当n为奇数时，中位数是唯一的；当n为偶数时，中位数有两个。问题简单的说就是：求数组中第i小的元素。

       那么问题来了：如何求一个数组里第i小的元素呢？

       常规方法：可以首先进行排序，然后取出中位数。由于排序算法（快排，堆排序，归并排序）效率能做到Θ(nlogn),所以，效率达不到线性；  在本文中将介绍两种线性的算法，第一种期望效率是线性的，第二种效率较好，是在最坏情况下能做到线性效率。见下面两个小节；

    2、方法一：以期望线性时间做选择                                       

    这是一种分治算法：以快速排序为模型：随机选取一个主元，把数组划分为两部分，A[p...q-1]的元素比A[q]小，A[q+1...r]的元素比A[q]大。与快速排序不同，如果i=q，则A[q]就是要找的第i小 的元素，返回这个值；如果i < q，则说明第i小的元素在A[p...q-1]里；如果i > q，则说明第i小的元素在A[q+1...r]里；然后在上面得到的高区间或者低区间里进行递归求取，直到找到第i小的元素。

    下面是在A[p...q]中找到第i小元素的伪码：

    1 RandomSelect(A,p, q,k)//随机选择统计，以期望线性时间做选择
2 {
3     if (p==q) return A[p];
4     int pivot=Random_Partition(A,p,q);//随机选择主元，把数组进行划分为两部分
5     int i=pivot-p+1;
6     if (i==k )return A[pivot];
7     else if (i<k) return RandomSelect(A,pivot+1,q,k-i);//第k小的数不在主元左边，则在右边递归选择
8     else return RandomSelect(A,p,pivot-1,k);//第k小的数不在主元右边，则在左边递归选择
9 }

    在最坏情况下，数组被划分为n-1和0两部分，而第i个元素总是落在n-1的那部分里，运行时间为Ө(n^2);但是，除了上述很小的概率情况，其他情况都能达到线性；在平均情况下，任何顺序统计量都可以在线性时间Θ(n)内得到。

    实现代码（c++）：

     1 //template<typename T>使用模板，可处理任意类型的数据
 2 template<typename T>//交换数据
 3 void Swap(T &m,T &n)
 4 {
 5     T tmp;
 6     tmp=m;
 7     m=n;
 8     n=tmp;
 9 }
10 
11 /***********随机快速排序分划程序*************/
12 template<typename T>
13 int Random_Partition(vector<T> &A,int p,int q)
14 {
15     //随机选择主元，与第一个元素交换
16     srand(time(NULL));
17     int m=rand()%(q-p+1)+p;
18     Swap(A[m],A[p]);
19     //下面与常规快排划分一样
20     T x=A[p];
21     int i=p;
22     for (int j=p+1;j<=q;j++)
23     {
24         if (A[j]<x)
25         {
26             i=i+1;
27             Swap(A[i],A[j]);
28         }
29     }
30     Swap(A[p],A[i]);
31     return i;
32 }
33 /***********随机选择统计函数*************/
34 template<typename T>
35 T RandomSelect(vector<T> &A,int p,int q,int k)//随机选择统计，以期望线性时间做选择
36 {
37     if (p==q) return A[p];
38     int pivot=Random_Partition(A,p,q);//随机选择主元，把数组进行划分为两部分
39     int i=pivot-p+1;
40     if (i==k )return A[pivot];
41     else if (i<k) return RandomSelect(A,pivot+1,q,k-i);//第k小的数不在主元左边，则在右边递归选择
42     else return RandomSelect(A,p,pivot-1,k);//第k小的数不在主元右边，则在左边递归选择
43 }
    View Code

    3、方法二（改进）：最坏情况线性时间的选择                       

          相比于上面的随机选择，我们有另一种类似的算法，它在最坏情况下也能达到O(n)。它也是基于数组的划分操作，而且利用特殊的手段保证每次划分两边的子数组都比较平衡；与上面算法不同之处是：本算法不是随机选择主元，而是采取一种特殊的方法选择“中位数”，这样能使子数组比较平衡，避免了上述的最坏情况（Ө(n^2)）。选出主元后，后面的处理和上述算法一致。

         那么问题又来了，这种特殊的手段是什么呢？

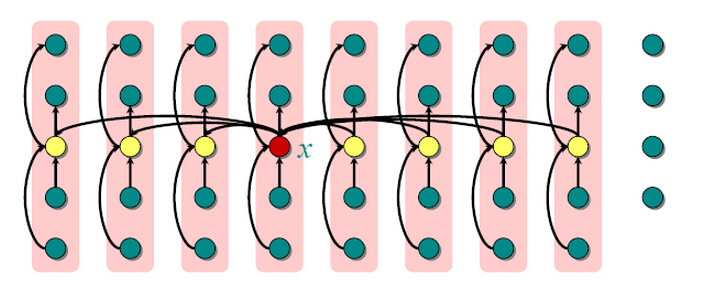
    如上图所示：

    1） 将输入数组的n个元素划分为n/5组，每组（上图中的每列为一组）5个元素，且至多只有一个组有剩下的n%5个元素组成

    2）  首先对每组中的元素（5个）进行插入排序，然后从排序后的序列中选择出中位数（图中黄色数）。

    3） 对第2步中找出的n/5个中位数，递归调用SELECT以找出其中位数x（图中红色数）。（如果有偶数个中位数取较小的中位数）

    这三个步骤就可以选出一个很好的主元，下面的处理和方法一一致（递归）

    OK! 下面是完整的算法步骤：

    1）  将输入数组的n个元素划分为n/5组，每组（上图中的每列为一组）5个元素，且至多只有一个组有剩下的n%5个元素组成

    2）  首先对每组中的元素（5个）进行插入排序，然后从排序后的序列中选择出中位数（图中黄色数）。

    3） 对第2步中找出的n/5个中位数，递归调用SELECT以找出其中位数x（图中红色数）。（如果有偶数个中位数取较小的中位数）

    4） 调用PARTITION过程，按照中位数x对输入数组进行划分。确定中位数x的位置k。

    5） 如果i=k，则返回x。否则，如果i<k，则在地区间递归调用SELECT以找出第i小的元素，若干i>k，则在高区找第(i-k)个最小元素。

    大致伪码：

     1 WorseLinearSelect(vector<T> &A,int p,int q,int k)
 2 {
 3     // 将输入数组的n个元素划分为n/5（上取整）组，每组5个元素，
 4     // 且至多只有一个组有剩下的n%5个元素组成。
 5     if (p==q) return A[p];
 6 
 7     int len=q-p+1;
 8     int medianCount=1;
 9     if (len>5)
10         medianCount = len%5 >0 ? len/5 + 1 : len/5;
11     vector<T> medians(medianCount);//存放每组的中位数
12 
13     // 寻找每个组的中位数。首先对每组中的元素（至多为5个）进行插入排序，
14     // 然后从排序后的序列中选择出中位数。
15     int m=p;
16     for (int j=0,m=p;j<medianCount-1;j++)
17     {
18         medians[j] = GetMedian(A,m,m+4);
19         m+=5;
20     }
21     medians[medianCount-1] = GetMedian(A,m,q);
22     //对第2步中找出的n/5（上取整）个中位数，递归调用SELECT以找出其中位数pivot。
23     //（如果是偶数去下中位数）
24     int pivot = WorseLinearSelect(medians,0,medianCount-1,(medianCount+1)/2);
25     //调用PARTITION过程，按照中位数pivot对输入数组进行划分。确定中位数pivot的位置r。
26     int r = partitionWithPivot(A,p,q,pivot);
27     int num = r-p+1;
28     //如果num=k，则返回pivot。否则，如果k<num，则在地区间递归调用SELECT以找出第k小的元素，
29     //若干k>num，则在高区找第(k-num)个最小元素。
30     if(num==k) return pivot;
31     else if (num>k) return WorseLinearSelect(A,p,r-1,k);
32     else return WorseLinearSelect(A,r+1,q,k-num);
33 }

    该算法在最坏情况下运行时间为Θ(n)

    代码实现(c++)：

      1 template<typename T>//插入排序
  2 void insertion_sort(vector<T> &A,int p,int q)
  3 {
  4     int i,j;
  5     T key;
  6     int len=q-p+1;
  7     for (j=p+1;j<=q;j++)
  8     {
  9         i=j-1;
 10         key=A[j];
 11         while (i>=p&&A[i]>key)
 12         {
 13             A[i+1]=A[i];
 14             i--;
 15         }
 16         A[i+1]=key;
 17     }
 18 }
 19 /*
 20  *    利用插入排序选择中位数
 21  */
 22 template<typename T>
 23 T GetMedian(vector<T> &A,int p,int q)
 24 {
 25     insertion_sort(A,p,q);//插入排序
 26     return A[(q-p)/2 + p];//返回中位数,有两个中位数的话返回较小的那个
 27 }
 28 /*
 29  *    根据指定的划分主元pivot来划分数组
 30  *    并返回主元的顺序位置
 31  */
 32 template<typename T>
 33 int  partitionWithPivot(vector<T> &A,int p,int q,T piovt)
 34 {
 35     //先把主元交换到数组首元素
 36     for (int i=p;i<q;i++)
 37     {
 38         if (A[i] == piovt)
 39         {
 40             Swap(A[i],A[p]);
 41             break;
 42         }
 43     }
 44     //常规的快速排序划分程序
 45     //
 46     T x=A[p];
 47     int i=p;
 48     for (int j=p+1;j<=q;j++)
 49     {
 50         if (A[j]<x)
 51         {
 52             i=i+1;
 53             Swap(A[i],A[j]);
 54         }
 55     }
 56     Swap(A[p],A[i]);
 57     return i;
 58 }
 59 /*
 60  *    最坏情况下线性时间选择算法
 61  *    此算法依然是建立在快速排序的划分算法基础之上的
 62  *    但是与randomizedSelect算法的不同指之处，就是次算法的本质
 63  *    是保证了每次划分选择的划分主元一定是一个较好的主元，算法先对数组5个一组进行分组
 64  *    然后选择每组的中位数，再递归的选择各组中位数中的中位数作为数组的划分主元，以此保证划分的平衡性
 65  *    选择中位数的时候必须使用递归调用的方法才能降低时间复杂度
 66  *    从而保证在最坏情况下都得到一个好的划分
 67  *    最坏情况下时间复杂度为O(n)
 68  */
 69 template<typename T>
 70 T WorseLinearSelect(vector<T> &A,int p,int q,int k)
 71 {
 72     // 将输入数组的n个元素划分为n/5（上取整）组，每组5个元素，
 73     // 且至多只有一个组有剩下的n%5个元素组成。
 74     if (p==q) return A[p];
 75 
 76     int len=q-p+1;
 77     int medianCount=1;
 78     if (len>5)
 79         medianCount = len%5 >0 ? len/5 + 1 : len/5;
 80     vector<T> medians(medianCount);//存放每组的中位数
 81 
 82     // 寻找每个组的中位数。首先对每组中的元素（至多为5个）进行插入排序，
 83     // 然后从排序后的序列中选择出中位数。
 84     int m=p;
 85     for (int j=0,m=p;j<medianCount-1;j++)
 86     {
 87         medians[j] = GetMedian(A,m,m+4);
 88         m+=5;
 89     }
 90     medians[medianCount-1] = GetMedian(A,m,q);
 91     //对第2步中找出的n/5（上取整）个中位数，递归调用SELECT以找出其中位数pivot。
 92     //（如果是偶数去下中位数）
 93     int pivot = WorseLinearSelect(medians,0,medianCount-1,(medianCount+1)/2);
 94     //调用PARTITION过程，按照中位数pivot对输入数组进行划分。确定中位数pivot的位置r。
 95     int r = partitionWithPivot(A,p,q,pivot);
 96     int num = r-p+1;
 97     //如果num=k，则返回pivot。否则，如果k<num，则在地区间递归调用SELECT以找出第k小的元素，
 98     //若干k>num，则在高区找第(k-num)个最小元素。
 99     if(num==k) return pivot;
100     else if (num>k) return WorseLinearSelect(A,p,r-1,k);
101     else return WorseLinearSelect(A,r+1,q,k-num);
102 }
    View Code

    4、完整测试代码（c++）                                                  

    完整源码下载地址Github

    Select.h

      1 #ifndef SELECT_HH
  2 #define SELECT_HH
  3 template<typename T>
  4 class Select
  5 {
  6 public:
  7     T RandomSelect(vector<T> &A,int p,int q,int k);//期望线性时间做选择
  8     T WorseLinearSelect(vector<T> &A,int p,int q,int k);//最坏情况线性时间的选择
  9 private:
 10     void Swap(T &m,T &n);//交换数据
 11     int Random_Partition(vector<T> &A,int p,int q);//随机快排分划
 12     void insertion_sort(vector<T> &A,int p,int q);//插入排序
 13     T GetMedian(vector<T> &A,int p,int q);
 14     int partitionWithPivot(vector<T> &A,int p,int q,T piovt);//根据指定主元pivot来划分数据并返回主元的顺序位置
 15 };
 16 
 17 template<typename T>//交换数据
 18 void Select<T>::Swap(T &m,T &n)
 19 {
 20     T tmp;
 21     tmp=m;
 22     m=n;
 23     n=tmp;
 24 }
 25 
 26 /***********随机快速排序分划程序*************/
 27 template<typename T>
 28 int Select<T>::Random_Partition(vector<T> &A,int p,int q)
 29 {
 30     //随机选择主元，与第一个元素交换
 31     srand(time(NULL));
 32     int m=rand()%(q-p+1)+p;
 33     Swap(A[m],A[p]);
 34     //下面与常规快排划分一样
 35     T x=A[p];
 36     int i=p;
 37     for (int j=p+1;j<=q;j++)
 38     {
 39         if (A[j]<x)
 40         {
 41             i=i+1;
 42             Swap(A[i],A[j]);
 43         }
 44     }
 45     Swap(A[p],A[i]);
 46     return i;
 47 }
 48 /***********随机选择统计函数*************/
 49 template<typename T>
 50 T Select<T>::RandomSelect(vector<T> &A,int p,int q,int k)//随机选择统计，以期望线性时间做选择
 51 {
 52     if (p==q) return A[p];
 53     int pivot=Random_Partition(A,p,q);//随机选择主元，把数组进行划分为两部分
 54     int i=pivot-p+1;
 55     if (i==k )return A[pivot];
 56     else if (i<k) return RandomSelect(A,pivot+1,q,k-i);//第k小的数不在主元左边，则在右边递归选择
 57     else return RandomSelect(A,p,pivot-1,k);//第k小的数不在主元右边，则在左边递归选择
 58 }
 59 
 60 template<typename T>//插入排序
 61 void Select<T>::insertion_sort(vector<T> &A,int p,int q)
 62 {
 63     int i,j;
 64     T key;
 65     int len=q-p+1;
 66     for (j=p+1;j<=q;j++)
 67     {
 68         i=j-1;
 69         key=A[j];
 70         while (i>=p&&A[i]>key)
 71         {
 72             A[i+1]=A[i];
 73             i--;
 74         }
 75         A[i+1]=key;
 76     }
 77 }
 78 /*
 79  *    利用插入排序选择中位数
 80  */
 81 template<typename T>
 82 T Select<T>::GetMedian(vector<T> &A,int p,int q)
 83 {
 84     insertion_sort(A,p,q);//插入排序
 85     return A[(q-p)/2 + p];//返回中位数,有两个中位数的话返回较小的那个
 86 }
 87 /*
 88  *    根据指定的划分主元pivot来划分数组
 89  *    并返回主元的顺序位置
 90  */
 91 template<typename T>
 92 int  Select<T>::partitionWithPivot(vector<T> &A,int p,int q,T piovt)
 93 {
 94     //先把主元交换到数组首元素
 95     for (int i=p;i<q;i++)
 96     {
 97         if (A[i] == piovt)
 98         {
 99             Swap(A[i],A[p]);
100             break;
101         }
102     }
103     //常规的快速排序划分程序
104     //
105     T x=A[p];
106     int i=p;
107     for (int j=p+1;j<=q;j++)
108     {
109         if (A[j]<x)
110         {
111             i=i+1;
112             Swap(A[i],A[j]);
113         }
114     }
115     Swap(A[p],A[i]);
116     return i;
117 }
118 /*
119  *    最坏情况下线性时间选择算法
120  *    此算法依然是建立在快速排序的划分算法基础之上的
121  *    但是与randomizedSelect算法的不同指之处，就是次算法的本质
122  *    是保证了每次划分选择的划分主元一定是一个较好的主元，算法先对数组5个一组进行分组
123  *    然后选择每组的中位数，再递归的选择各组中位数中的中位数作为数组的划分主元，以此保证划分的平衡性
124  *    选择中位数的时候必须使用递归调用的方法才能降低时间复杂度
125  *    从而保证在最坏情况下都得到一个好的划分
126  *    最坏情况下时间复杂度为O(n)
127  */
128 template<typename T>
129 T Select<T>::WorseLinearSelect(vector<T> &A,int p,int q,int k)
130 {
131     // 将输入数组的n个元素划分为n/5（上取整）组，每组5个元素，
132     // 且至多只有一个组有剩下的n%5个元素组成。
133     if (p==q) return A[p];
134 
135     int len=q-p+1;
136     int medianCount=1;
137     if (len>5)
138         medianCount = len%5 >0 ? len/5 + 1 : len/5;
139     vector<T> medians(medianCount);//存放每组的中位数
140 
141     // 寻找每个组的中位数。首先对每组中的元素（至多为5个）进行插入排序，
142     // 然后从排序后的序列中选择出中位数。
143     int m=p;
144     for (int j=0,m=p;j<medianCount-1;j++)
145     {
146         medians[j] = GetMedian(A,m,m+4);
147         m+=5;
148     }
149     medians[medianCount-1] = GetMedian(A,m,q);
150     //对第2步中找出的n/5（上取整）个中位数，递归调用SELECT以找出其中位数pivot。
151     //（如果是偶数去下中位数）
152     int pivot = WorseLinearSelect(medians,0,medianCount-1,(medianCount+1)/2);
153     //调用PARTITION过程，按照中位数pivot对输入数组进行划分。确定中位数pivot的位置r。
154     int r = partitionWithPivot(A,p,q,pivot);
155     int num = r-p+1;
156     //如果num=k，则返回pivot。否则，如果k<num，则在地区间递归调用SELECT以找出第k小的元素，
157     //若干k>num，则在高区找第(k-num)个最小元素。
158     if(num==k) return pivot;
159     else if (num>k) return WorseLinearSelect(A,p,r-1,k);
160     else return WorseLinearSelect(A,r+1,q,k-num);
161 }
162 #endif
    View Code

    main.cpp

     1 #include <iostream>
 2 #include <vector>
 3 #include <time.h>
 4 using namespace std;
 5 #include "Select.h"
 6 #define  N 10   //排序数组大小
 7 #define  K 100   //排序数组范围0～K
 8 ////打印数组
 9 void print_element(vector<int> A)
10 {
11     int len=A.size();
12     for (int i=0;i<len;i++)
13     {
14         std::cout<<A[i]<<" ";
15     }
16     std::cout<<std::endl;
17 }
18 int main()
19 {
20     Select <int> s1;
21     int a[10]={23,4,34,345,3,21,45,246,98,50};
22     vector<int> vec_int(a,a+10);
23     cout<<"原始数组"<<endl;
24     print_element(vec_int);
25     // 期望线性时间做选择测试
26     cout<<"期望线性时间做选择测试"<<endl;
27     for(int i=1;i<=N;i++)
28     {
29         int kMin=s1.RandomSelect(vec_int,0,N-1,i);
30         cout<<"第"<<i<<"小的数是："<<kMin<<endl;
31     }
32     //最坏情况线性时间的选择测试
33     cout<<"最坏情况线性时间的选择测试"<<endl;
34     for(int i=1;i<=N;i++)
35     {
36         int kMin=s1.WorseLinearSelect(vec_int,0,N-1,i);
37         cout<<"第"<<i<<"小的数是："<<kMin<<endl;
38     }
39     system("PAUSE");
40     return 0;
41 }
    View Code

    5、参考资料                                                                    

    【1】http://blog.csdn.net/xyd0512/article/details/8279371

    【2】http://blog.chinaunix.net/uid-26822401-id-3163058.html

    【3】http://www.tuicool.com/articles/mqQBfm

    【4】http://www.cnblogs.com/Anker/archive/2013/01/25/2877311.html
  • 相关阅读:
    12306是如何实现高流量高并发的关键技术
    阿里知名工程师
    侵入式和非侵入式的区别
    二叉树节点的最大距离
    2014阿里面经（转）
    jq checkbox的相关操作——全选、反选、获得所有选中的checkbox
    表现和数据分离的好处
    css3完成多边形
    程序员，如何从平庸走向理想？--转载
    js对象和字符串相互转换
  • 原文地址：https://www.cnblogs.com/zhoutaotao/p/4047082.html
Copyright © 2020-2023  润新知