[HDU5772]String problem

vjudge

题意

给你一个0~9组成的字符串，你可以从中选取一个子序列（或者说一个集合）。
如果位置(i,j)同时被选，就可以获得(w[i][j])的收益。
对于每一种数字，设其被选的次数为(k_i)，那么你需要对这个数字付出的代价为

[A_i(k_i-1)+B_i (k_i>0)\0 (k_i=0) ]

求最大收益。

sol

考虑一个点对(i,j)。如果它要选，那么(i)，(j)就必须都要选。(i)，(j)都选那么对应的数值就都要选。
所以可以按照如下方式建边。（假设(i)对应的数字是(0)，(j)对应的数字是(1)）

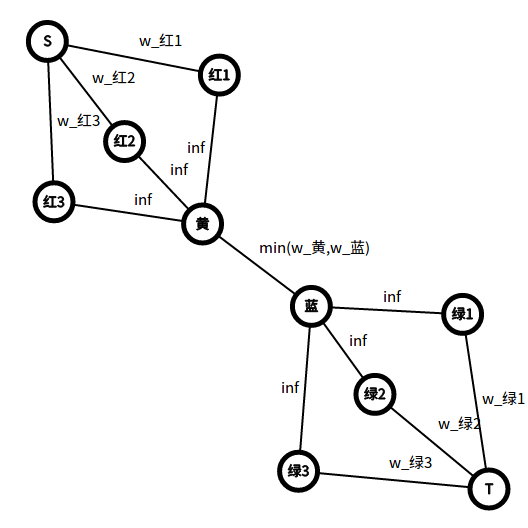
不能拉长QAQ
其中数字向汇点连的边其实就是表示这种数字选了(0)次。
所以就是一个最大权闭合子图的问题。
图中一共是(frac{n(n-1)}{2}+n+10+2)个点。

code

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
int gi()
{
	int x=0,w=1;char ch=getchar();
	while ((ch<'0'||ch>'9')&&ch!='-') ch=getchar();
	if (ch=='-') w=0,ch=getchar();
	while (ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
	return w?x:-x;
}
const int N = 10005;
const int inf = 1e9;
struct edge{int to,nxt,w;}a[N<<5];
int Case,n,tot,w[105][105],A[N],B[N],S,T,head[N],cnt=1,dep[N],cur[N],ans;
char s[N];
queue<int>Q;
void link(int u,int v,int w)
{
	a[++cnt]=(edge){v,head[u],w};
	head[u]=cnt;
	a[++cnt]=(edge){u,head[v],0};
	head[v]=cnt;
}
bool bfs()
{
	memset(dep,0,sizeof(dep));
	dep[S]=1;Q.push(S);
	while (!Q.empty())
	{
		int u=Q.front();Q.pop();
		for (int e=head[u];e;e=a[e].nxt)
			if (a[e].w&&!dep[a[e].to])
				dep[a[e].to]=dep[u]+1,Q.push(a[e].to);
	}
	return dep[T];
}
int dfs(int u,int f)
{
	if (u==T) return f;
	for (int &e=cur[u];e;e=a[e].nxt)
		if (a[e].w&&dep[a[e].to]==dep[u]+1)
		{
			int tmp=dfs(a[e].to,min(a[e].w,f));
			if (tmp) {a[e].w-=tmp;a[e^1].w+=tmp;return tmp;}
		}
	return 0;
}
int Dinic()
{
	int res=0;
	while (bfs())
	{
		for (int i=1;i<=T;++i) cur[i]=head[i];
		while (int tmp=dfs(S,inf)) res+=tmp;
	}
	return res;
}
void init()
{
	memset(head,0,sizeof(head));cnt=1;
	ans=0;tot=0;
}
int main()
{
	Case=gi();
	for (int zsy=1;zsy<=Case;++zsy)
	{
		init();
		n=gi();S=n*(n-1)/2+n+10+1;T=S+1;
		scanf("%s",s+1);
		for (int i=0;i<10;++i) A[i]=gi(),B[i]=gi();
		for (int i=1;i<=n;++i)
			for (int j=1;j<=n;++j)
				ans+=(w[i][j]=gi());
		for (int i=1;i<=n;++i)
			for (int j=i+1;j<=n;++j)
			{
				++tot;
				link(S,tot,w[i][j]+w[j][i]);
				link(tot,n*(n-1)/2+i,inf);
				link(tot,n*(n-1)/2+j,inf);
			}
		for (int i=1;i<=n;++i)
		{
			link(n*(n-1)/2+i,n*(n-1)/2+n+s[i]-'0'+1,inf);
			link(n*(n-1)/2+i,T,A[s[i]-'0']);
		}
		for (int i=0;i<10;++i)
			link(n*(n-1)/2+n+i+1,T,B[i]-A[i]);
		printf("Case #%d: %d
",zsy,ans-Dinic());
	}
	return 0;
}