利率

利息虽然随处可见，但还是经常让我很困惑。这章我们就详细讨论一下利润的行为为什么如此古怪。

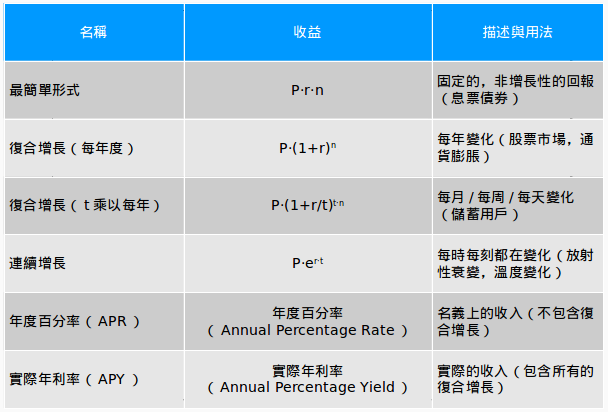
理解它们的概念有助于我们理解财政（按揭与储蓄），通过无处不在的e与自然对数，我们列出了下表帮助学习：

9.1 为什么要大惊小怪呢？

利率很复杂。就像罗马数字与象形文字一样，虽然可以“用”，但是效果并不理想。

在刚开始的时候，你有100个金币，你每年可以的收益是12%（Percent＝Per Cent＝Per Hundred——看看，到处都有罗马数字的身影！）。这很简单：每年可以获得12个金币的收入。但是真的是12吗？

如果我们把它分解开来看，好像是我们一个月赚一个金币：一月到六月赚六个金币，七月到十二月又赚六个金币。但是等一等——但是六月份结束后，在七月份我们就有了106个金币，但是接下来它们只能赚六个金币吗？你是在告诉我半年的时间100个金币赚得钱跟106个金币赚得钱一样多？根据逻辑推断，100个金币跟200个金币能赚得一样多吗？

但是这个问题好像并没有困扰古埃及人，但是17世纪时确实发现了这个问题，并且直接导致伯努利（Bernoulli）发现了e（这里对数学爱好者说声抱歉。e的发现并不是因为它具有逼近某个极限的性质而被发现的）。关于这个问题有太多东西可以说了——但是记住，我们是在分析利率：

利率与其它专业术语在复合发明之前就有了。真是的！带宽大概是在16世纪出现的，出现在指数，0，甚至是小数点之前！所以我们的讨论会让人困惑其实很正常。

自然不会等到一个人类年后才开始改变。利息收入也是一种形式的“增长”，但是温度与放射性衰变等每时每刻都在发生变化。这就是为什么物理方程使用“e”而不是“(1+r)ⁿ”:自然发生变化时只会无视我们的日历。

9.2 学学行话

因为这些难题的缘故，我们需要引进一些新的术语：

年度百分率（APR）：就是别人告诉你的利率（“每年12%！”）。你会看到公式中有个r。

实际年利率（APY）：就是你一年后实际获得收益的百分比，包括计算复利在内。在公式中你可以把它当作“总收入”。APY肯定不比APR差。

APR是银行告诉你的，而APY是你实际得到的（扣除各种税费，杂七杂八的手续费后，你应该懂我的意思）。当然银行总是向你展示那个更好看的数字。

办信用卡或是准备汽车贷款？银行会向你展示只需要支付“低APR”来掩盖更高的APY。但是开一个储蓄帐户？他们当然会向你展示“高APY”，来让他们看起来很慷慨。

APY才是你真正需要关心的，你只需要通过对比它来做出选择就好了。

9.3 简单的利息

让我们从最底层开始吧：最简单的利息是每年付给你固定数额的钱。这是一些例子：

伊索寓言中那个会下金蛋的鹅：那只鹅每天都下一个金蛋。不会更快，而且金蛋也不会生出小鹅来继续产金蛋。

公司债券：一张面值为1000元，利率为5%的债权每年付给你50元直到它过期。你不可能增加面值金额，所以每年你只能拿到50元（现实生活中，债权每六个月给你25元）。

最简单的利息也是一种最基础的收益。在银行中存入100元，年利率为50%，那么画出图来就是：

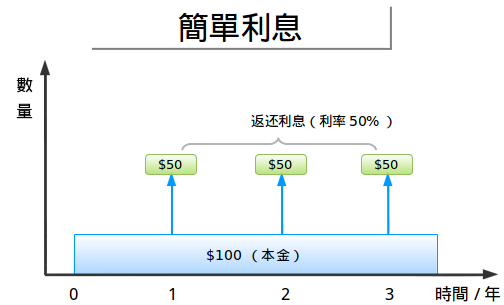
你最开始的资本（也叫作投资）是100元，然后每年赚50元。

我假设蓝色部分就是你的“投入”，而上面的绿色部分就是每年产出的部分。

然而，这些新的绿色钱是固定不变的——它不能继续生钱！按照最简单的利息计算，50元就在那里不变了。能生钱的只有那最开始的100元钱。

最简单利息计算有一个最简单的公式：每隔一段时间你就能赚到 P·r（资本·利率）。经过n段时间后你就有：

收益＝P·r·n

只要r和n在同一段时间内，这个公式就可以使用。它可以几年，几个月甚至是几天——在大多数情况下，我们通常是按年计算。因为没有复利（利息不能产生利息）所以其中没有任何复杂的东西。

这种利息在以下情形下很有用：

你的利息不能再继续产生利息。这就像那只会下金蛋的鹅，或者是公司债券能获得收入但是不能再投资。

你希望得到简单，可预测的，非指数的结果。加入你在鼓励孩子储蓄的话。你可以告诉孩子们每放20元到小猪储蓄罐，每月就可以得到1元的“乐趣钱”。许多孩子每个月都喜欢买些漫画书。如果他/她是格林斯潘家族的话，他/她可能会要求把收益也投资进去。

在实践中，这种利息计算很少见，因为大多数收益都可以进行再投资。如果你的收益不能改变的话，就没有APR与APY的区别了：你每年赚到的钱都是一样的。

9.4 真正的理解增长

许多关于利息的解释到这里就停住了：这就是公式，套进去用就好了。而不是在这里：让我们看看到底发生了什么。

首先，利率到底是什么意思呢？我认为它是一种“速度”：

50迈就是说在一小时的时间内你前进了50英里。

r＝每年50%就是说你经过一年内可以收入你资本的50%。如果P＝100元，那么你每年就赚到50%（你的“钱的增长速度”）。

但是两种类型的速度都有一个共同的地方：我们不必等到整个时间周期结束！

以50迈的速度行驶时不时就是说你必须走够一小时？显然不是！你可以“只”行驶半个小时，向前行驶25英里（50·0.5）。你也可以走15分钟，向前行进12.5英里（50·0.25）。你明白了吧。

利息也与之类似。利率给了你一条“轨道”或是“速度”来计算。如果你投入100元，而利率是每年50%的最简利息，那么你的速度就是每年50元。但是你不一定非要等这一年结束！如果只过了半年，那么你就获得了25元。看看下面这幅图：

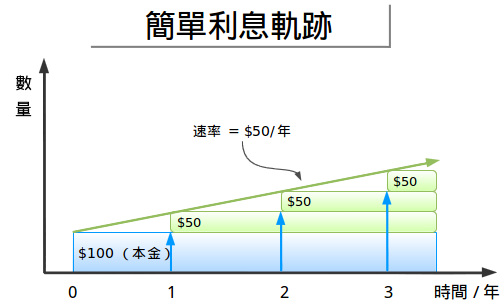
我们刚开始有100元，用蓝色表示。每年蓝色部分都贡献50元钱。当然，因为是按照最简单的利息计算，我们的收益始终是基于我们最开始的资本计算的，而不是“新的总资本”。把那些点连起来就看到了其中趋势：我们始终保持着50元/年的速度。我们的收入看起来像是一个阶梯，那是因为我们只能在每年结束时才能获得收益，但是“速度”依然有效。

最简单的利息计算法保持着相同的轨迹：不管怎样我们每年收入“P·r”（在上面这个例子中是每年50元），那条直线非常准确的预测了将来的走势。

“遵从一个轨迹”看起来看你有些怪，但是先接受它吧——后面它将帮助我们理解e的本性。

一个要点：那个轨迹就是银行账户在一个确定的时间会以“多快的速度”增长。在最简单利息的情况下，我们保持恒速：每年50元或者说是50迈。在其它例子中，我们的利率会发生变化，就像跳伞运动员：刚开始速度比较慢，但是以后将越来越快。但是在任意一个时刻，他们都有一个唯一的速度，一个单一的轨迹。

（数学老师会告诉你这个轨迹称为“微分”或是“梯度”。但是在这里并不需要用到微积分，因为太过大材小用了。）

9.5 基本的复利计算

最基本的利息计算可能让你很不爽。为什么我们的收益不能继续赚钱呢？我们应该用债券收益（每年50元）去购买更多的债券。就是嘛！我们可以用鹅下的金蛋去资助克隆金蛋的研究。

复利就是指你的利息还可以产生利息。爱因斯坦把它称作“自然界中的一股强大力量”，而事实确实如此。有一个东西在增长，增长出来的东西继续增长，子子孙孙无穷尽也……你的收益也可以快速增加。

最基本的形式是周期式的收益，这通常意味着按年计算。按年重新投资我们的收益，画出图来就是：

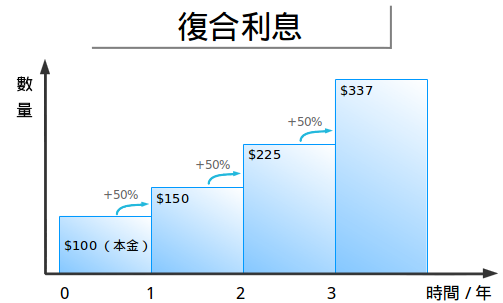
在0-1年我们获得了50元的收益，就像最简单利息那样。但是在1-2年，我们现在总共有150元，所以这一年我们可以赚到75元（150·0.5），然后在2-3年我们总共有225元，再赚到它的50%，那就是112.5元。

更一般的情况，我们每年都有有(1+r)倍多的东西。n年之后，就变为：

收益＝P·（1+r）ⁿ

指数增长很快超过了简单的线性增长，线性增长3年只有3（100+3*50）的收入。复合增长在以下情形很有用：

利息可以进行再投资，大多数银行帐户都可以这么做。

你希望基于一个增长的趋势来预测未来。许多趋势，比如说通货膨胀，GDP增长等等，都被假设为“可以符合的”。每年增长3%的GDP，十年后就变为（1.03）¹⁰＝1.344，或者说是经过十年后增长了34.4%。

9.6 把利息当作一个工厂

通常人们习惯把金钱看作一个随着时间增长会不断扩大的“斑点”。这种观点当然可行，但是我喜欢把利息收益看作是一个可以继续生钱的“工厂”：

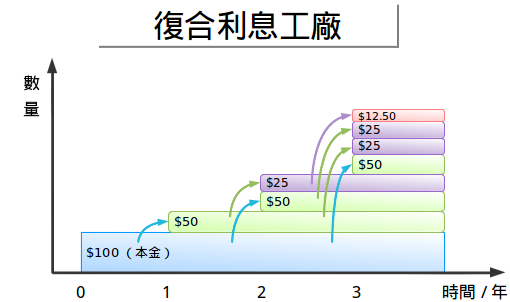
这就是所发生的一切：

第0年：我们有100元钱。

第1年：我们的100元产出了50元的收益

第2年：最初的100元又生出了50元，而之前的50元也生出了25元。最后总共有50+25＝75元，符合情况。

第3年：开始变得复杂起来了。最初的100元又生出了第三个50元。而之前的两个50元也各生出了25元，与此同时之前的25元也生出了12.5元。

第四年直到无穷：给读者当作一个练习吧（你不喜欢教科书逃避责任吗？）

这是一种很有趣的观点。100元一不小心就生出了一个“50元工厂”，它们各自独立的产生新的钱（注意那三个从蓝色资本指向绿色资本的蓝色箭头）。这些50工厂又产出了25工厂，这样一直进行下去。

这种模式看起来很复杂，但是换个角度其实很简单。最初的100元钱并不知道那些小50元钱们会做什么：100元钱只知道我每年产生50元的收益而已。

那么为什么这个观点很有用呢？

你可以把100元的作用与它的孩子们区别开来。举个例子，第三年时我们总共有328元。父母总共赚了150元（“3·50%·100＝150”，用最简单利息的计算公式）。而那些“孩子么＝们”的贡献就是328-150-100＝128元，也就是总价值的1/3。

把收益分开有助于帮助我们理解e。对e了解的更多一些很有好处，因为它出现在各种场合。

9.7 理解轨迹

哦，我们还没完成呢。再看看——看看我们的轨迹：

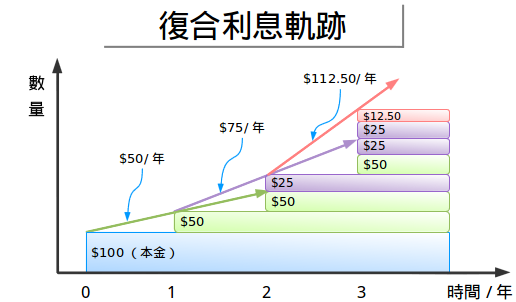
如果是最简单利息，我们一直保持着相同的速度（每年50元，好无聊啊！）。但是对于按年计算的复利，我们每年得到的轨迹都不一样。

我们存钱，然后就去睡觉，每年结束时醒来就会发现：

第一年：“嘿，等等。我有150元啊！我应该能赚到75元而不是50元。”你冲着银行家大吼，然后调高收益到每年75元，然后继续去睡觉。

第二年：“嘿，我有225元啊，我应该每年赚112.5元！”。你在银行大声喊叫，并促使他们调高了收益。

这个过程不断重复——好像我们永远等不到尽头。

9.8 再看复利

为什么要等这么长时间呢？没错，一次等一年比等“永远”（就像是最简单的利息计算）要好多了，但是我想我们可以更进一步，让我们把一年放大：

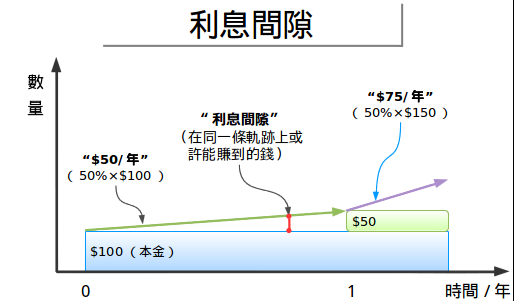
看看发生了什么。绿色的线代表我们刚开始的速度（每年50元），固定的区域表示我们帐户里的钱。六个月后，我们后我们本应该赚到25元，但是我们根本没见到！更重要的是，再过六个月后我们的轨迹依然与刚开始时一样。利息间隙告诉我们哪里应该赚到钱，但是依然保持原轨迹（基于我们最开始的资本）。我们正在失去我们本应该赚到的钱。

假设我借了你的钱，然后半年后我再还给你。“你看，我并没有借够一整年，所以我没有欠你任何利息。毕竟，利息是按年计算的嘛。按年年年。而不是按半年。”你看你会笑一笑，然后找人把我的腿打断。

按年支付是人造的产物，本意是为了让事情简单。但是在现实生活中，钱应该是每时每刻都能继续生钱的。我们可以每半年支付一次利息来减少利息间隙：

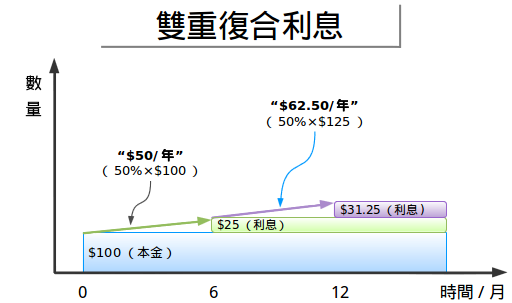
这就是发生了什么：

我们最开始有100元，然后保持每年50元的轨迹，更平常一样

六个月后我们赚到了25元，现在我们有125元

我们启用新的轨迹：50%·125＝62.5元/年

再过六个月我们就有62.5·0.5＝31.25元。现在我们共有156.25元。

关键点是每过半年我们的轨迹就改变一次，因而我们就赚到了156.25元而不是“预期的”150元。同样的，更早的取出利息帮助我们缩小利息间隙（途中白色区域），因为我们的25元在后半年也开始发挥作用继续生钱（它贡献了25·25%·0.5＝6.25元）。

以一年为例，最终的效果应该是r复合t得到的：

（1+r/t）^t

在我们例子中，我们有（1+50%）²。n年不断重复（乘以n倍）就得到：

收益＝P·（1+r/t）^t·n

复利减少了我们的钱不生钱的“死区域”。我们越频繁计算复利，赚取利息与改变轨迹的间隙就越小。

9.9 连续增长

很显然我们希望钱能尽可能的尽快发挥作用。连续增长就是服用了兴奋剂的复合增长利息：通过把一年分为无限多的小部分就可以把利息间隙缩小到没有：

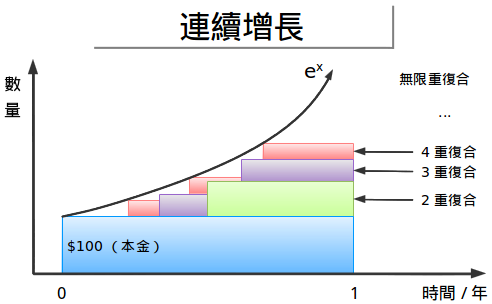
最后的效果就是利息刚一产生就能继续生出利息。我们等上百万分之一秒，然后就得到了新的总和，然后就产生了新的轨迹。除非不是在百万分之一秒，而是在每一毫微秒，每一皮秒，每一飞秒甚至是我也不知道该怎么称呼的更短时间间隔内它就产生了。连续增长的轨迹始终与你现在的总金额保持同步。

回顾一下关于e的那一章。如果我们有增长率r与时间t（在一年内），最后的结果就是：

收益＝P·e^r·t

如果你又50%的APR，那你的APY按照连续复利计算的话应该就是e^50%-1＝64.9%。这之间的区别相当大！注意，e搞定了难产的部分，比如说把时间无限分割。

为什么这个很有用呢？

许多自然想象都是连续增长的。正如之前所提到的，物理现象有着它自己的进程：放射性物质可不会根据地球环绕太阳的运动来决定是否衰变。任何物理方程涉及到模型变化通常都会用到：e^rt。

e^rt是可以进行调整的，而且它是个万金油式的指数。听起来很奇怪，但是e可以适用于我们之前见到的跳跃式的，阶梯式的复合增长。

许多利息讨论都不会用到e，因为在现实的财政计算中通常不会考虑连续增长。（按日进行福利计算，（1+r/365）³⁶⁵已经足够让你变得很富有了。不过按日计算复利确实是对连续增长一个很好的近似。

指数e是连接连续增长与跳跃式增长的一道桥梁。

9.10 一些例子

让我们举几个例子以加深理解吧。记住：APR是他们给你的，APY才是你真正得到的。

4.5的APY比4.4的APR好吗，按照季度计算复利？你需要比较APY与按照4.4%计算复利的APY。（1+4.4%/4）⁴＝4.47%。所以4.5的APY更好一些。

我应该在月初还是月末支付贷款利息呢？肯定是月初。这样你就可以更早的避免一大堆债务，避免“债务工厂”在接下来的30天内给你产生利息。假设你的贷款APY是6%，而你每月还2000元。如果你月初还款的话，你就节省了2000·6%＝120元/年，如果是 30年期的话，你总共就节省了3600元。省一点是一点嘛。

我应该是多次小额支付，还是一次性全额支付？你想尽快还清贷款。每周还500元比一个月还2000元钱好。每一次还款都减少了若干星期的利息。做这个计算需要一些小技巧，但是把它当作4次投资，每次投资都可以获得一定的收入。在一个月中，第一次还款省下了3个星期的利息：500·（1+每日利率）²¹。下一次又省下两个星期：500·（1+每日利率）¹⁴。第三次又省下了一个星期：500·（1+每日利率）⁷，最后的支付就什么也没省了。不管细节怎样，这样支付会给你省下不少钱。

基本原则：投资的时候，越早拿到收益就可以越早进行复利投资，而偿还债务时就要尽量避免计算复利。

9.11 向前也向上

这章有很多小细节，但是我希望你不要忽视了整体情况：

利率（APR）就是钱增长的“速度”。

计算复利让你不断根据赚到的钱来调整“速度”。APR是初始速度，APY才是最终速度。

人造物使用（1+r）ⁿ，或者是其它变量。我们希望我们的债务保持线性增长。

自然使用e^rt。宇宙不关心我们的日历。

利率很狡猾。当你看到疑惑时，查查APY，尽早还债。

费这么大劲（又是轨迹，又是工厂的）来学习利率可以帮助我们更好的理解e的性质，我们在微积分中还会用到e。同样的，利用72法则来快速心算以下利率的效果（6%的APY可以在12年内翻倍）。希望你能享受到快乐的数学。

《更好的解释（数学篇）》——第九章

利率