虛數
虛數這個概念經常讓我感到困惑。就像是理解e一樣,許多解釋基本上都可以歸為這兩類:
- 這是一種數學抽象,這是方程式產生的結果,隻管接受它就行了。
- 這個將用在高級物理中,相信我們吧,等你到了大學你就明白了。
專家們,這真是一種激勵孩子們積極好學的方法啊!今天就讓我們用我麼最喜歡的工具來攻克它吧:
- 關註其中的關係,而不是機械化的方程式。
- 把復數當作我們原有數字系統的升級版,就像0,十進制和負數那樣。
- 使用可視化的圖表,而不隻是文字,來理解這個概念。
還有我們的秘密武器:通過類比來進行學習。我們通過對比它的先輩,負數,來進行學習。以下就是你的指南書:
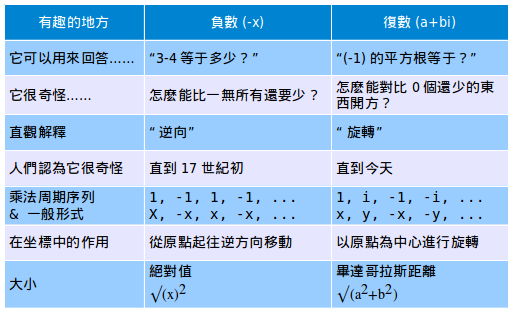
看起來好像沒什麼意義,但是先把它放一邊。到最後我們將先抓到它,然後再攻克它,而不是反之。
5.1 真正的理解負數
負數並不簡單。假設你是18世紀的一名歐洲數學家。你有3和4,你知道4-3=1。很簡單。
但是3-4呢?這,到底,意味著什麼呢?你怎麼能從3頭奶牛中拿走4頭?你怎們能擁有比空無一物更少的東西呢?
負數被認為是荒謬的,甚至被認為“導致整個數學都黯淡無光”(Francis Maseres,1759年)。但是在今天,認為負數符合邏輯或者是有用的並不荒謬。試著問問你的老師負數是否毀壞了數學的根基。
到底發生了什麼呢?我們引入了一種有著一些有用性質的理論數字。我們摸不到,也抓不住負數,但是它很好的描述了一些確定的關係(比如債務)。這是一個很有用的虛構。
相比說“我欠你30元”,然後看看文字確認到底是你欠我還是我欠你,我可以直接寫下“-30”,這樣我就知道是我欠你了。如果我賺到了錢,還請了債務(-30+100=70),我可以很容易的記錄這筆交易。我還剩下70元,這意味著我已經沒有負債了。
正負標記可以自動的幫我們記錄方向——你不要一一判斷每筆交易。數學可以讓這更簡單,更優雅。負數是“有形還是無形”其實無所謂——它們有著一些有 用的性質,直到它們真正進入我們的生活我們才把它們發揮的淋漓盡致。如果你沒有“得到”負數的話,你就會背上惡名(obscene name,應該是指美國的信用卡消費文化——譯者註)。
但是我們不應自以為是:負數是一次智力的大飛躍。即使是歐拉,那位發現了e以及其他東西的天才數學家,也不像我們今天這樣瞭解負數。負數被認為是“沒有意義”的結果(最後他也隨大流接受了這樣的結果)。
這隻是一個簡單的證明,告訴我們今天的孩子們的智力應該可以更容易接受這些觀點,即使這些觀點曾經讓很多數學前輩們很是困惑。
5.2 進入虛數的世界
虛數也有一個類似的故事。我們可以很輕易的解出以下方程:
x2 =9
答案是3和-3。但是加入有一個聰明人加入了一個小小的負號呢:
x2 =-9
哦。許多人第一次見到這個方程就退縮了。你想把一個比零還小的數字開平方,這是荒謬絕倫的。
這看起來很瘋狂,就像負數,0,還有無理數(非重復數字)首次被引入時一樣瘋狂。這個方程並沒有什麼“實在”意義,對吧?
錯了。所謂的“虛數”就像其他數字一樣正常(即使它們也是被造出來的):它們是描述世界的一種工具。就像假設-1,0.3,0“真實存在”一樣,讓我們也假設一些i存在吧:
i2 =-1
這就是,你把i自乘兩次就得到-1.接下來會發生什麼呢?
首先我們會頭疼。讓我們玩個“假裝i存在”的游戲吧,這樣可以讓數學更簡單,更優雅。這樣其中的關係就可以很容易的浮現出來了。
你或許不相信i的存在,就像那些老前輩們不相信-1的存在一樣。現在是一個新的讓我們難以理解的概念,現在還看不出有什麼意義,即使是歐拉也沒有。但是正如負數告訴我們的,怪異的概念一樣可以有用。
我不喜歡“想像出來的數”這種稱呼——這是一種設計好的侮辱,誹謗,故意傷害i的感情。i就像其他數字一樣正常,但是“虛數”這個名字既然一直沿用下來了,我們隻好繼續使用。
5.3 以一種可視化的方法理解負數與復數
方程式x2 =9也可以表示成:
1·x2 =9
x應該是什麼,使得它自乘兩次後,1變成了9?
兩個答案就是“x=3”與“x=-3”:這就是,你“乘以3”或者“乘以3,然後翻轉”(翻轉或取反是乘以負數的另一種解釋)。
接下來讓我們考慮以下x2 =-1,這其實就是:
1·x2 =-1
x應該是什麼,可以使它自乘兩次後,1變為-1?
- 我們不可能乘以一個正數,因為乘以正數以後還是正數
- 我們不能乘以一個負數兩次,因為相乘兩次後又會變為正數。
但如果是……旋轉呢!這聽起來很瘋狂,但是如果我們假設x被“轉過了90度”,然後乘以x兩次那就是旋轉180度,也就是把1翻轉成了-1!
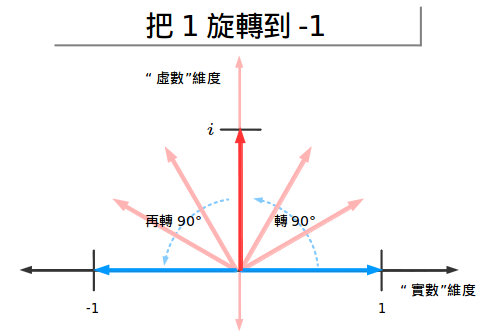
耶!讓我們繼續深入考慮下去,我們可以把它繞其他方向旋轉(比如說順時針方向)來從1變為-1.這就是“負向”旋轉或者是稱作乘以-i:
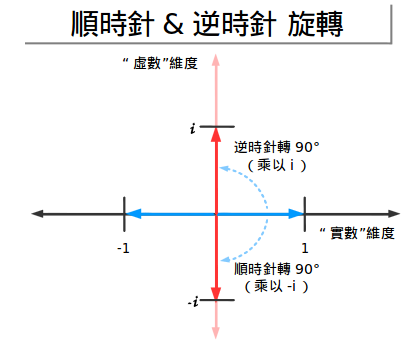
如果我們乘以-i兩次,我們把1變成-i,然後-i變成-1,所以-1確實存在兩個根:i與-i。
這個很酷。我們有一些答案,但是這說明了什麼呢?
- i是一個“新的想像出來的維度”,來標記數字
- i(或者-i)就是指數字“被旋轉”
- 乘以i就是沿逆時針方向旋轉90度
- 乘以-i就是沿順勢正方向旋轉90度
- 無論那個方向,旋轉兩次就是-1:這就把我帶回到“傳統”的正負維度上去了。
數字是二維的。是的,這樣可能有些難以理解,這就像讓古羅馬人理解十進制與長除法一樣(你說1和2之間還有數字是什麼意思?)。
我們會問“怎樣通過兩步,把1變成-1”,然後我們就找到了答案:把它旋轉90度。這確實是一個奇怪但是又讓我們耳目一新的方法來理解數學。而且它很有用。(順便提一下,這種用幾何的方法解釋復數的方法直到i被發現幾十年後才被引入)
此外,逆時針為正是人們的一個約定俗成習慣——其他表示也是可以的。
5.4 發現其中的模式
讓我繼續深入細節。當我們連續乘以負數時(比如說-1),你就得到一種模式:
1,-1,1,-1,1,-1……
因為-1並不改變數的大小,隻改變符號,你就這樣的反復進行翻轉。比如說數“x”,你就會得到:
x,-x,x,-x,x,-x……
這個點子很有用。x可以代表好的或壞的髮型。假設每週都輪流變換;這周是好髮型周,那麼47周會是什麼周呢?
x·-147 =x·-1=-x
那麼-x就意味著壞髮型周。註意到負數是怎樣“保持符號的軌跡的”——我們可以直接在計算器中輸入“-147 ”而不用一步一步計算(1周是好的,2周是壞的,三週是好的…………)。通過運用負數這一切隻是反復翻轉而已。
Ok。現在讓我們看看如果乘以i後會發生什麼?
1,i,i2 ,i3 ,i4 ,i5 ……
非常搞笑。讓我們化簡一下:
- 1=1(毫無疑問)
- i=i(已經很簡單了)
- i2 =-1(這是i的定義)
- i3 = (i·i)·i=-1·i=-i(啊哈,逆時針旋轉3次=一次旋轉,很簡單)
- i4 = (i·i)·(i·i) =-1·-1=1(四次旋轉就是一個完整的圓)
- i5 = i4 · 1=i(接下來再來一次)
用圖表示出來就是:
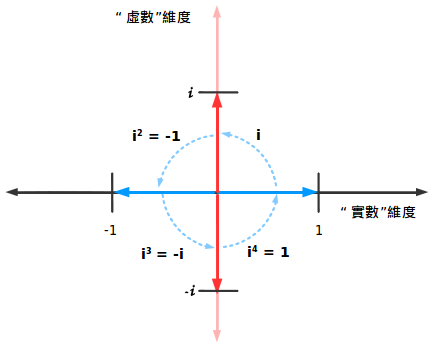
每四次旋轉循環一次。這就有意義了,對吧?小孩子都可以告訴你旋轉四次跟沒有旋轉一樣。與其關註虛數(i,i2 ),不如看看更一般的模式:
X,Y,-X,-Y,X,Y,-X,-Y……
就像負數一樣翻轉,虛數可以模仿任何在兩個維度之間旋轉的東西。或者是任何遵循週期或環形關係的東西——你想到些什麼了嗎?
cos與sin,如果你沒有想到的話,後面我們還會提到於這個有關的棣美弗定理(De Moivre Theorem)[編輯註:Kalid正在接受電擊治療以治療他喜愛使用雙關語]
5.5 理解復數
這裏還有另外一個細節需要揭示:一個數字可以既是“實的”又是“虛的”嗎?
確實能。誰說我們必須旋轉90度?如果我們一隻腳在實數範圍內,另一隻在虛數範圍內,就像這樣:
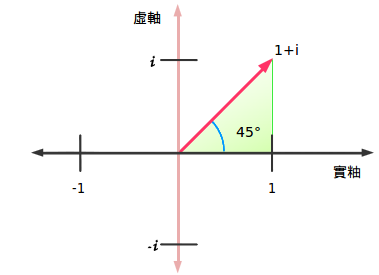
我們處在45度角的為止,實數部分的大小與虛數部分的大小相當(1+i)。這就像一個熱狗既有芥末醬也有番茄醬——誰說你隻能選一種的?
事實上,我們可以任意選取實數與虛數組成一個三角形。角度就是“旋轉的度數”。復(合)數就是給這種數字准備的一個相當完美的名字。它們寫作 a+bi,其中
- a是實數部分
- b是虛數部分
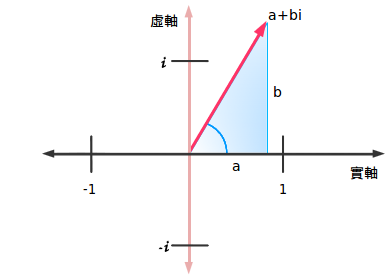
目前為止還不錯。但是還有最後一個問題:復數有多“大”呢?我們不能單獨測量實數部分或是虛數部分,因為我們忽略了整體。
讓我們再退回去看看。負數的大小不是指你能把它數到多少——而是它距離零點的距離。因此負數的距離就是負數的平方再開根。
這是另一種計算絕對值大小的方法。但是對於復數,我們在90度的時候我們怎麼測量兩部分?
這是隻鳥……這是飛機……這是畢達哥拉斯!
老天啊,他的理論真是到處都有,即使是在他2000年以後發明的數字中。對,我們構造一些三角形,然後斜邊就是它到零點的距離:
a+bi的大小等於a與b平方和再開根
非常幹凈。雖然計算復數的大小並不像負數那樣去掉負號就可以了,但是它有它的用處。讓我們來看一看。
5.6 示例:旋轉
我們不會等到去大學物理中學習虛數。我們現在就學學吧。關於復數相乘有很多內容,但是把這個切記於心中:
乘以一個復數就是繞著它旋轉
讓我們先來看一看。假設我在一艘小船上,船頭的指向是向東3個單位,向北四個單位。我想把船頭指向逆時針旋轉45度。新的指向朝向哪裏呢?
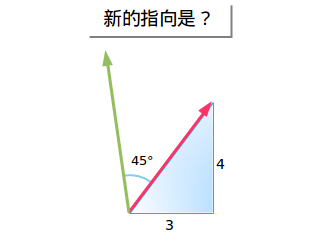
有些能人會說“很簡單嘛,用正余弦函數,切線Blahblah……消去變量什麼的……”真要命。對不起,我打斷你的計算了嗎?能再回答一次這個問題嗎?
讓我試一種更簡單的方法:我們的指向是3+4i(無所謂角度是什麼,我們並不關心),然後我們想旋轉45度角。那麼45度角就是1+i,那麼我們乘以它就好了!
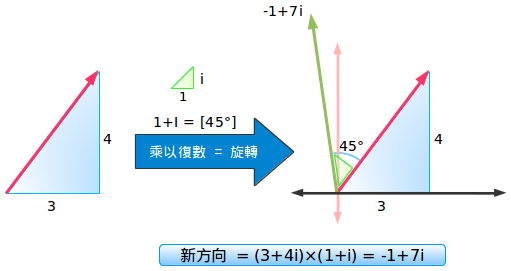
這就是要點:
- 原始指向:向東3個單位,向北4個單位=3+4i
- 逆時針旋轉45度角後的指向=乘以1+i
如果我們把它們相乘便得到:
(3+4i)(1+i)=3+4i+3i+4i2 =3-4+7i=-1+7i
那麼我們的新指向就是向西(-1倍的向東)1個單位,向北7個單位,你可以很輕鬆的把它畫出來。
哦耶,我們花了不到10秒就把它找了出來,並且沒有使用正余弦函數。沒有向量,沒有矩陣,或者是
關心我們在哪個象限。隻是簡單的算術,涉及到一些代數與十字相乘而已。虛數天生就有旋轉規則:而且很有效。
更好的一點是,結果很有用。我們用指向(-1,7)取代了角度(arc tan(7/-1)=98.13,記住我們在第二象限)。然而我們怎樣准確的畫出這個角度呢?一直帶著量角器嗎?
不用這樣,你可以把它們轉變成正余弦函數(-0.14與0.99),然後找出一個合適的比例(從1到7),然後畫出那個角度。復數可以以更加快速,准確的方法畫出它,而且不需要計算器。
如果你喜歡它,那麼這是一個非常棒的結果,如果你不喜歡,那麼我很抱歉,數學並沒能吸引你。
三角法是很有用,但是復數可以讓複雜的計算變得簡單(就像計算cos(a+b)那樣)。這隻是一個預告而已;下一章將給你一頓更加豐盛的大餐。
5.7 復數不是“無稽之談”
復數確實改變了我的基本觀念。現在再回頭看一看第一張圖表——你應該能理解不少東西了。
還有不少這樣漂亮、荒唐的數字,但是現在我累了。我的目標很簡單那:
- 讓你相信復數並不是“無稽之談”,而是很有處的(就像負數那樣)
- 復數怎樣讓一些問題更簡單,比如旋轉
如果在這個話題中看起來很激動,並且有些焦慮,那是有原因的。虛數就像一個蜜蜂一樣一直在我身邊困擾了我許多年——一直缺少一種直觀的理解讓我很沮喪。
現在我終於直到怎樣以一種更加直觀的方法理解它,我強烈希望與你分享這些觀點。我們經常被一些問題困擾著,有時隻能囫圇吞棗的接受它。這些發現就是我在黑暗中的一些小小燭光;你也會發現照亮自己的小小燭光。
還有許多復數:在下一章中學習一下復數的元算。希望你能享受到快樂的數學。
5.8 結尾:但是它們看起來還是很奇怪
我知道,我現在看它們也很奇怪。我試著把自己想像成第一個發現零的人。
零是這樣奇怪的一個概念,有些“東西”代表“什麼也沒有”,羅馬人逃避了這個概念。復數也類似——這是一種新的思考方式。無論是零還是復數都讓數學更加簡單。如果我們永遠不接納怪異的,新的數字系統,我們可能現在還在依靠手指計數呢。
我不斷的重復類比是因為這樣考慮復數很“正常”就比較容易了。讓我們保持一種開放的心態:在未來他們或許會對我們被復數所困擾而咯咯笑,即使實在二十一世紀。
本網站無註明「轉載」的著作均由Jak Wings製作 CC BY-NC-SA 2.5
Creative Commons 保持署名-相同方式分享 2.5
原文地址:http://jakwings.is-programmer.com/posts/29547.html