深度优先搜索简称深搜,从起点出发,走过的点要做标记,发现有没走过的点,就随意挑一个往前走,走不了就回退,此种路径搜索策略就称为“深度优先搜索”,简称“深搜”。
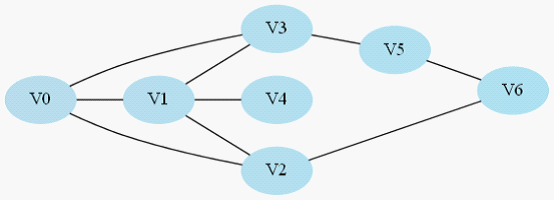
如上面的图所示:加入我们要找一个从V0到V6的一条最短的路径。我们可以看到有许多的路我们可以走。
V0——V3——V5——V6;
V0——V3——V1——V4;
V0——V3——V1——V2——V6;
V0——V1——V4;
V0——V1——V3——V5——V6;
V0——V1——V2——V6;
V0——V2——V6;
前两组,是从节点V3开始分的,然后遍历了后面的所有路径,然后找到了我们需要的解。
从第三条路径我们就可以看到,到了V4之后就没有路了,那么我们就需要返回到V1找下一条路径。
V1节点所有的路径我们就都找完了,就开始找V2节点的路径了。由于我们一开始不知道哪一条路可以走到V6和不知道哪一条路径最短,所以我们需要找出所有的路,然后再来判断哪一条路最短。
上面我们找到了所有的路径,然后判断最小的路径是V0——V2——V6,这就是最优解。
深搜的基本模板:
int search(int t) { if(满足输出条件) { 输出解; } else { for(int i=1;i<=尝试方法数;i++) if(满足进一步搜索条件) { 为进一步搜索所需要的状态打上标记; search(t+1); 恢复到打标记前的状态;//回溯 } } }
总结:深搜就是要找到所有可能的解,然后再来找到最优解,需要我们遍历所有的路径。
典型例题(八皇后):链接:https://www.luogu.org/problem/P1219
题目描述
检查一个如下的6 x 6的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。

上面的布局可以用序列2 4 6 1 3 5来描述,第i个数字表示在第i行的相应位置有一个棋子,如下:
行号 1 2 3 4 5 6
列号 2 4 6 1 3 5
这只是跳棋放置的一个解。请编一个程序找出所有跳棋放置的解。并把它们以上面的序列方法输出。解按字典顺序排列。请输出前3个解。最后一行是解的总个数。
输入格式
一个数字N (6 <= N <= 13) 表示棋盘是N x N大小的。
输出格式
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
输入输出样例
6
2 4 6 1 3 5 3 6 2 5 1 4 4 1 5 2 6 3 4
对于该题目,因为我们不知道怎样来放这个点,所以我们需要将所有的点都试一下,防止漏掉哪一个点:
题解:
#include<iostream> using namespace std; int sum=1; int A[200]={0},B[200]={0},C[200]={0},D[200]={0};//表示横行,B表示纵行,C表示左下到右上的对角线,D表示左上到右下的对角线 int n; int print()//输出前三个 { if(sum<=3) { for(int i=1;i<=n;i++) cout<<A[i]<<" "; cout<<endl; } sum++; } void dfs(int i) { if(i>n) { print(); return ; } if(i<=n) { for(int j=1;j<=n;j++) { if(B[j]!=1&&C[j-i+n]!=1&&D[i+j]!=1) { A[i]=j;//记录纵列的值 B[j]=1;//标记纵列 C[j-i+n]=1;//标记对角线 D[i+j]=1;//标记对角线 dfs(i+1);//接着搜下一个点 B[j]=0;//清除记忆 C[j-i+n]=0; D[j+i]=0; } } } } int main() { cin>>n; dfs(1); cout<<sum-1; return 0; }