摘要
姿态图优化的目的是根据相对姿态测量的约束来估计机器人的轨迹。由于室内环境中的磁场在时域中是稳定的,而在空间域中是足够变化的,因此我们可以利用这些特性来生成姿态图的约束。在本文中,我们提供了一种通过采用姿态图优化和室内磁测量来解决同时定位和制图(SLAM)问题的方法。具体而言,分别设计了用于局部航向校正和全局环路闭合的不同类型的约束。特别是对于环路闭合约束,我们首先检查室内磁场的空间相似性,并验证使用测量序列而不是单个测量可以减轻磁测量的歧义。然后根据磁测量的顺序提出闭环算法,并将其应用于姿态图优化。实验结果表明,所提出的仅具有车轮编码器和单个磁力计的SLAM系统在机器人轨迹方面可以与参考级SLAM系统获得可比的结果,从而验证了将磁约束应用于室内姿态图SLAM的可行性。
磁力优化闭环检测,能理解。局部航向矫正就不太懂了。
#这一点似乎就是VIO的东西了
First, we can extract local relative heading information from the magnetic measurements under certain situations of robot motions such as spinning. This renders additional self-motion constraints to the pose graph.
首先,我们可以在机器人运动(例如旋转)的某些情况下从磁测量值中提取局部相对航向信息。 这给姿势图带来了附加的自运动约束。
#磁力在回环检测时的作用
#单点测量有歧义,所以找一个系列的会比较好
Vallivaara等。 [15]在Rao–Blackwellized粒子滤波器的框架中显示了基于磁场的环路闭合。 他们根据磁场测量模型通过高斯过程对闭环粒子进行加权。 但是,它们在某些具有相似磁场的区域中无法闭合回路。 这是因为即使使用概率滤波方法,单点测量也不足以区分磁场的模糊性。 在这种情况下,采用一系列测量可以显着降低歧义度,如本文稍后所述。 然后可以基于磁测量的顺序设计闭环算法,并将其应用于优化。
作者考虑的是二维地图场景,优化目标就是位姿图,X = [x1,...xn],每个x都是一个pose
由于残差和雅可比行列式的计算取决于约束类型,因此我们可以将成本函数划分为相应的约束项。假设是地面车辆,姿态图通常具有两种类型的约束-里程表约束和闭合回路约束。成本函数E(x)可以描述为

这块我还不太懂公式,,不知道orb里面回环检测之后的BA是怎么做的。到底什么时候是完整的BA,什么时候仅仅是位姿图优化呢。
#如果没有平移只有旋转,磁力的变化会非常小,但是方向肯定会变吧,怎么比较呢,看不懂这个constraint要干嘛
#是不是如果满足了角度变化,位移没变化,那么要求两次测量的磁力也没变化,好像是这个意思
Additional constraints can be made by exploiting the measurement characteristics of the magnetic fields under certain conditions. Assuming our robot runs on a 2D plane, the magnetic field vector represented in a global coordinate frame should be stationary when the robot rotates without any translational displacement. Fig. 1 further illustrates this situation. Since this constraint is based on the magnetic measurements during the robot’s rotating motion, let us call it a magnetic pivoting (MP) constraint. In addition to the odometric constraints, the MP constraint is added to the pose graph whenever the following condition is satisfied:
通过利用某些条件下磁场的测量特性,可能会产生其他限制。假设我们的机器人在2D平面上运行,则当机器人旋转而没有任何平移位移时,以全局坐标系表示的磁场矢量应该是静止的。图1进一步说明了这种情况。由于此约束基于机器人旋转运动期间的磁测量值,因此我们将其称为磁枢轴(MP)约束。除了里程约束之外,只要满足以下条件,MP约束就会添加到姿势图中:

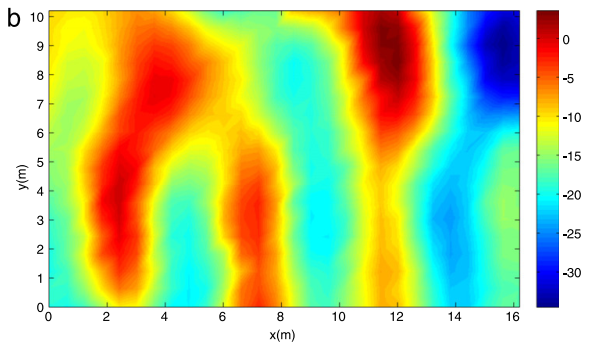
作者验证了下,磁力数据在室内分布的是不是足够有区分度。
画了几张图还是挺有区分度的,而且环境也不算小了,16mx10m.
机器人采的数据,但是measurement interval似乎有点大啊,30cm和60cm。
说到底,采集到的是一个向量,做区分的呢,既有大小又根据方向的
如果只有强度就有底下这种区分性的话,加上方向会更好区分吧
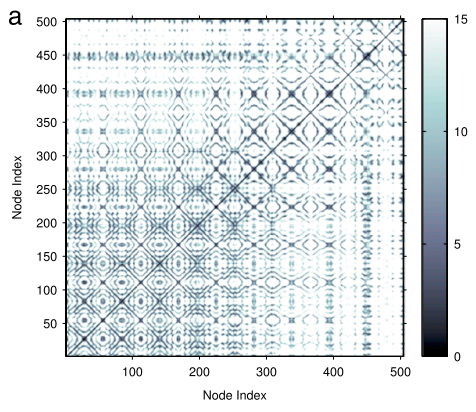
噢,还是算了个相似矩阵,如果不存在相似的点,矩阵就会呈现对角线为1的特性
实验先说明了,单个点匹配的情况下,欧氏距离比cosine距离好用
这两张图还挺体现作者的目的的,500个点可以被整成70条path。

As the robot moves along a linear path, a sequence of three-component magnetic measurements are grouped into a single vector si. The corresponding pose nodes are also grouped to generate a super node Xi.
把三个磁力记录聚成一个sequence;没有考虑斜线就很奇怪;emmmm;为什么不直接做一个search的方法呢,啊,其实,移动1米才变成一个sequence,还蛮远的
The reason for requiring a linear motion is that in this way we can restrain the magnetic fluctuation occurring by the robot’s orientation change, which enhances the matching performance. 为什么要直线走,因为旋转会让它没办法匹配,yes;磁力在这里还挺麻烦的。
match的方法是互相关,类似,
实验结果,好像比visual的还要好,作者在一个比较对视觉不友好的场景下作的实验