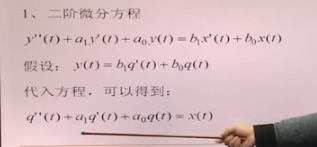3.0 引言
用正弦信号而不是冲激或阶跃作为子信号,用正弦信号之后到频域分析
3.2 信号的分解
类比向量的分解,可以用一组正交的函数,找到最佳的系数
用三角函数集
${1, cos(k omega T), sin(k omega T)}$, k 是正整数,$omega = frac{2 pi}{t2 - t1}$, t2 - t1就是信号区间的长度




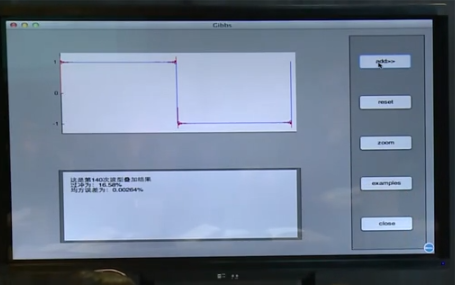
周期方波的傅里叶展开,有毛刺,名字叫过冲,Gibbs现象,函数的间断点附近一定会有这种现象
另一个三角函数集,包含复指数

周期信号傅里叶级数展开的谐波性。。。。。
信号时域参数对信号频谱的影响

3.5非周期信号的频谱
非周期=周期信号在周期趋向于无穷大的极限

论文里用花体F代表傅里叶变化,F-1代表反变换

3.8傅里叶变换的性质
线性特性(齐次,叠加
延时特性
移频特性
尺度变换:时域上压缩,频域上扩展,信号的脉冲宽度和频带宽度是对立的
奇偶虚实性
反折或者共轭
时域微分特性
时域积分特性
频域微积分特性
卷积特性:

功率谱和能量谱





第四章,频域上分析系统
卷积变成了乘法,幅度乘以幅度,相角加相角

可以通过系统的频域特性,傅里叶反变换计算系统的冲激响应





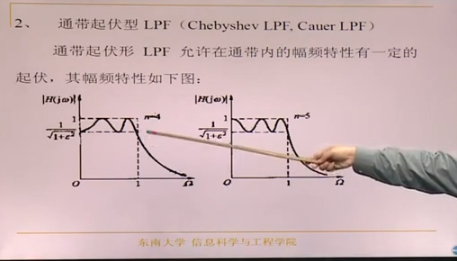
通带的起伏来换过渡带的宽窄,过渡带越窄越好
第四章的第二部分,调制与解调我没看
第五章,拉普拉斯变换
为什么需要拉普拉斯变换,傅里叶的不足




有些信号的拉氏变换不存在,例如直流,正弦等


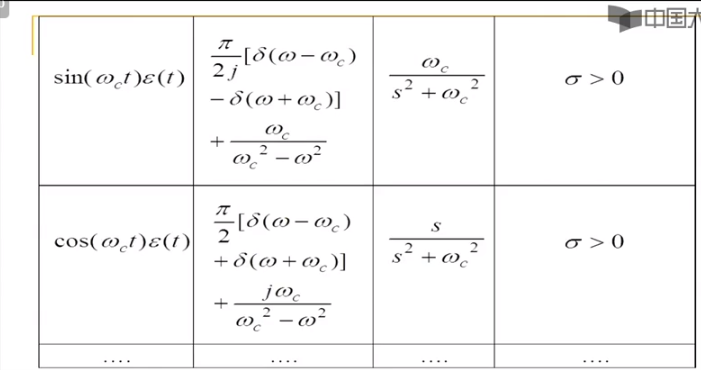


上面为0是0点,下面为0是极点
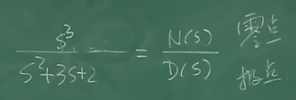

拉普拉斯变换性质
线性
尺度变换

延时特性(单边周期信号
移频特性
求系统响应= 等式两边同求拉氏变换


拉氏变换求零状态响应


H(s)一定是系统冲激响应的拉氏变换
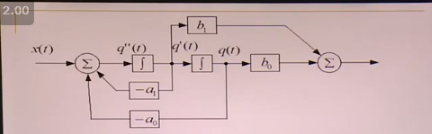
系统框图

积分器(从零时刻到当前时刻

积分器的另一种写法

怎么根据微分方程画信号框图
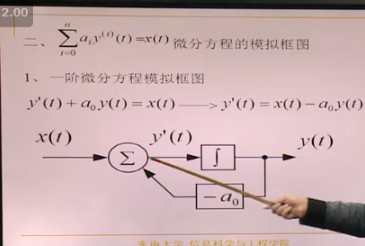
等式两边都存在微分的情况下:替换变量画框图