1.题目:
返回一个整数数组中最大子数组的和。
2.要求:
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
如果数组A[0]……A[j-1]首尾相邻,允许A[i-1], …… A[n-1], A[0]……A[j-1]之和最大。
同时返回最大子数组的位置。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
3.设计思想:
分情况讨论最大子数组可能出现的情况,第一种为正常情况,没有超过数组范围,第二种则比较复杂,要用到环的一部分元素,分而求出两种情况的最大值,进而比较大小就可以求得环形数组的最大子数组的和。
4.源代码:
1 #include<iostream.h>
2 int main()
3 {
4 int n,k;
5 int list[100000];
6 int max, min, sumMax, sumMin;
7 int total;
8 cout<<"输入数组长度:"<<endl;
9 cin>>n;
10 while(n!=0)
11 {
12 cin>>list[0];
13 max=sumMax=list[0]>0?list[0]:0;
14 min=sumMin=list[0]<0?list[0]:0;
15 total=list[0];
16 for(int i=1;i<n;i++)
17 {
18 cin>>list[i];
19 if(sumMax>0)
20 sumMax+=list[i];
21 else
22 sumMax=list[i];
23 if(sumMin<0)
24 sumMin+=list[i];
25 else
26 sumMin=list[i];
27
28 max=sumMax>max?sumMax:max;
29 min=sumMin<min?sumMin:min;
30 total+=list[i];
31 }
32 int tmp=total-min;
33 k=max>tmp?max:tmp;
34 cout<<"数组最大子数组和为:"<<k<<endl;
35 }
36 return 0;
37 }
5.结果截图:
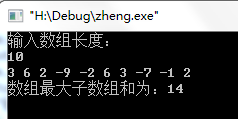
6.心得体会:
通过课上同学们的提醒和建议,我们组的思路也差不多,更多的是考虑到复杂度的要求,这是个比较棘手的问题。问题难不怕,怕的是懒得去思考,懒得去动手实现和解决这一问题,结对编程则很好的弥补了这一缺陷。
