
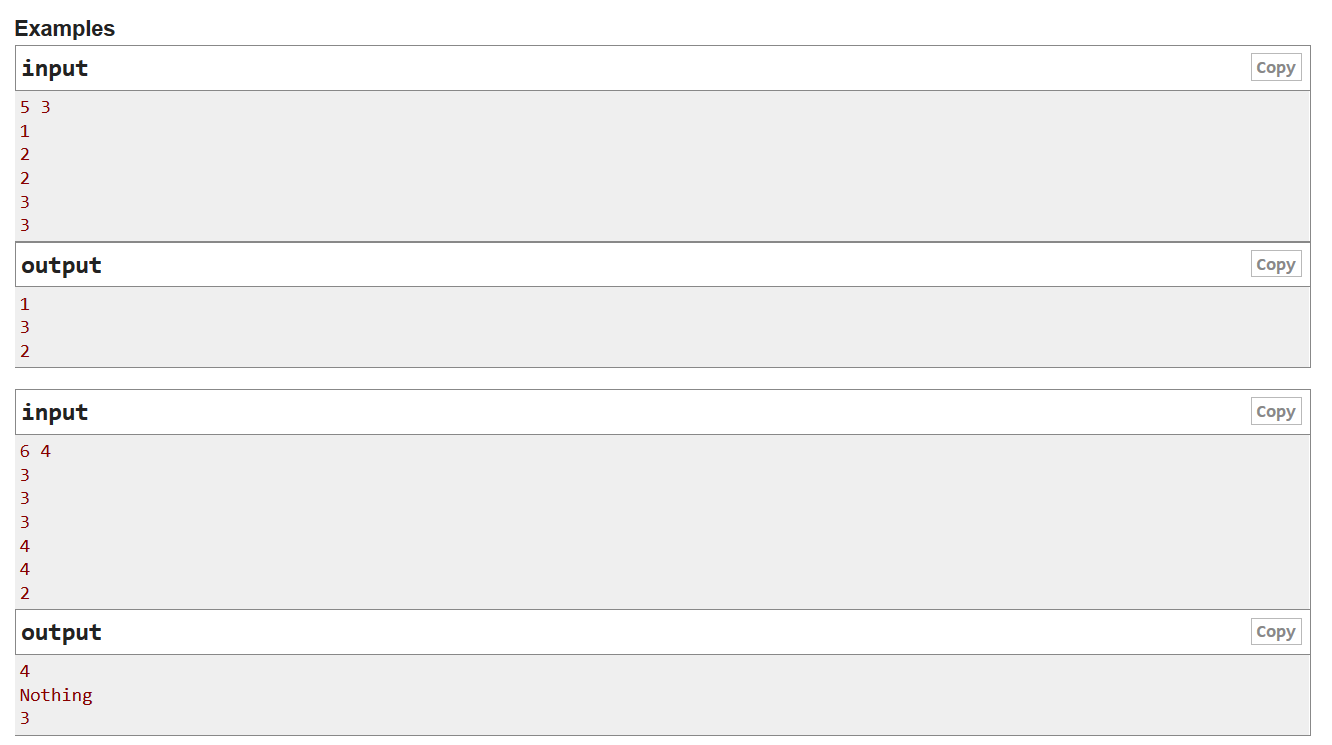
思路:
刚开始:
利用map来统计长度为k的一段上的数字及其出现次数,不断更新区段位置,减去退出区段的数字的出现次数,加上新出现的数字及其出现次数,每次都从后向前遍历一遍map,如果遇到一个数且出现次数为1,那么他就是当前区段上的最大数(因为map中已排好序),break,当前循环结束。这种方法果然想的太简单,超时
然后:问题出在哪?前面的不断更新和统计都是在log n时间完成的,应该没有问题。如果出现一种情况,在求当前区间最大值的时候,都是出现不止一次的数,就意味着要遍历整个map。
结果:利用set方便求最值,set自身也是一种树形结构,操作在log n内可以完成。因为set的元素不重样,我们只需将map中出现次数为1的数丢进set,每次更新区段时,先看退出的数出现次数是否减少到一,是则丢入set,不是看是不是在set中出现,如果出现就set中erase它,因为它的出现次数不为1,不在比较范围内。先加入元素看出现次数是否唯一,唯一加入set,不唯一看set中是否有,有就删除。再从set中选最大值,即最后一个(set已经排好序),一轮循环结束。
知识点:
set的insert,empty,end(),rend(),rbegin()(反向迭代器,十分方便)
map的[]访问方式
下面是代码:
1 #include <iostream> 2 #include <map> 3 #include <set> 4 #include <climits> 5 #define max_n 100005 6 using namespace std; 7 int a[max_n]; 8 map<int,int> num; 9 set<int> sets; 10 int n; 11 int k; 12 int main() 13 { 14 cin >> n >> k; 15 for(int i = 0;i<n;i++) 16 { 17 cin >> a[i]; 18 } 19 for(int i = 0;i<k;i++) 20 { 21 num[a[i]]++; 22 if(num[a[i]]==1) 23 { 24 sets.insert(a[i]); 25 } 26 else 27 { 28 if(sets.find(a[i])!=sets.end()) 29 { 30 sets.erase(a[i]); 31 } 32 } 33 } 34 if(sets.empty()) 35 { 36 cout << "Nothing" << endl; 37 } 38 else 39 { 40 auto i = sets.rbegin(); 41 cout << *i << endl; 42 } 43 int f = 0; 44 int b = k; 45 for(;b<n;f++,b++) 46 { 47 num[a[f]]--; 48 num[a[b]]++; 49 if(num[a[f]]==1) 50 { 51 sets.insert(a[f]); 52 } 53 else 54 { 55 if(sets.find(a[f])!=sets.end()) 56 { 57 sets.erase(a[f]); 58 } 59 } 60 if(num[a[b]]==1) 61 { 62 sets.insert(a[b]); 63 } 64 else 65 { 66 if(sets.find(a[b])!=sets.end()) 67 { 68 sets.erase(a[b]); 69 } 70 } 71 if(sets.empty()) 72 { 73 cout << "Nothing" << endl; 74 } 75 else 76 { 77 auto i = sets.rbegin(); 78 cout << *i << endl; 79 } 80 /*for(auto i = num.rbegin();i!=num.rend();i++) 81 { 82 cout << i->first << "-" << i->second << endl; 83 }*/ 84 } 85 }