实验四 决策树算法及应用

博客班级	班级链接
作业要求	作业链接
学号	3180701119
一、实验目的
1.理解决策树算法原理，掌握决策树算法框架；
2.理解决策树学习算法的特征选择、树的生成和树的剪枝；
3.能根据不同的数据类型，选择不同的决策树算法；
4.针对特定应用场景及数据，能应用决策树算法解决实际问题。

二、实验内容
1.设计算法实现熵、经验条件熵、信息增益等方法。
2.实现ID3算法。
3.熟悉sklearn库中的决策树算法；
4.针对iris数据集，应用sklearn的决策树算法进行类别预测。
5.针对iris数据集，利用自编决策树算法进行类别预测。

三、实验报告要求
1.对照实验内容，撰写实验过程、算法及测试结果；
2.代码规范化：命名规则、注释；
3.分析核心算法的复杂度；
4.查阅文献，讨论ID3、5算法的应用场景；

四、实验内容以及结果
In [1]:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter
import math
from math import log
import pprint

In [2]:

# 书上题目5.1
def create_data():
    datasets = [['青年', '否', '否', '一般', '否'],
                ['青年', '否', '否', '好', '否'],
                ['青年', '是', '否', '好', '是'],
                ['青年', '是', '是', '一般', '是'],
                ['青年', '否', '否', '一般', '否'],
                ['中年', '否', '否', '一般', '否'],
                ['中年', '否', '否', '好', '否'],
                ['中年', '是', '是', '好', '是'],
                ['中年', '否', '是', '非常好', '是'],
                ['中年', '否', '是', '非常好', '是'],
                ['老年', '否', '是', '非常好', '是'],
                ['老年', '否', '是', '好', '是'],
                ['老年', '是', '否', '好', '是'],
                ['老年', '是', '否', '非常好', '是'],
                ['老年', '否', '否', '一般', '否'],
                ]
    labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']
    # 返回数据集和每个维度的名称
    return datasets, labels

In [3]:

datasets, labels = create_data()

In [4]:

train_data = pd.DataFrame(datasets, columns=labels)

In [5]:

train_data

In [6]:

# 熵
def calc_ent(datasets):
    data_length = len(datasets)
    label_count = {}
    for i in range(data_length):
        label = datasets[i][-1]
        if label not in label_count:
            label_count[label] = 0
        label_count[label] += 1
    ent = -sum([(p / data_length) * log(p / data_length, 2)
            for p in label_count.values()])
    return ent
# def entropy(y):
# """
# Entropy of a label sequence
# """
# hist = np.bincount(y)
# ps = hist / np.sum(hist)
# return -np.sum([p * np.log2(p) for p in ps if p > 0])
# 经验条件熵
def cond_ent(datasets, axis=0):
    data_length = len(datasets)
    feature_sets = {}
    for i in range(data_length):
        feature = datasets[i][axis]
        if feature not in feature_sets:
            feature_sets[feature] = []
        feature_sets[feature].append(datasets[i])
    cond_ent = sum(
        [(len(p) / data_length) * calc_ent(p) for p in feature_sets.values()])
    return cond_ent
# 信息增益
def info_gain(ent, cond_ent):
    return ent - cond_ent

def info_gain_train(datasets):
    count = len(datasets[0]) - 1
    ent = calc_ent(datasets)
    # ent = entropy(datasets)
    best_feature = []
    for c in range(count):
        c_info_gain = info_gain(ent, cond_ent(datasets, axis=c))
        best_feature.append((c, c_info_gain))
        print('特征({}) - info_gain - {:.3f}'.format(labels[c], c_info_gain))
    # 比较大小
    best_ = max(best_feature, key=lambda x: x[-1])
    return '特征({})的信息增益最大，选择为根节点特征'.format(labels[best_[0]])

In [7]:

info_gain_train(np.array(datasets))

In [8]:

# 定义节点类 二叉树
class Node:
    def __init__(self, root=True, label=None, feature_name=None, feature=None):
        self.root = root
        self.label = label
        self.feature_name = feature_name
        self.feature = feature
        self.tree = {}
        self.result = {
            'label:': self.label,
            'feature': self.feature,
            'tree': self.tree
        }
    def __repr__(self):
        return '{}'.format(self.result)
    def add_node(self, val, node):
        self.tree[val] = node
    def predict(self, features):
        if self.root is True:
            return self.label
        return self.tree
class DTree:
    def __init__(self, epsilon=0.1):
        self.epsilon = epsilon
        self._tree = {}
    # 熵   
    @staticmethod
    def calc_ent(datasets):
        data_length = len(datasets)
        label_count = {}
        for i in range(data_length):
            label = datasets[i][-1]
            if label not in label_count:
                label_count[label] = 0
            label_count[label] += 1
        ent = -sum([(p / data_length) * log(p / data_length, 2)
                    for p in label_count.values()])
        return ent 
    # 经验条件熵
    def cond_ent(self, datasets, axis=0):
        data_length = len(datasets)
        feature_sets = {}
        for i in range(data_length):
            feature = datasets[i][axis]
            if feature not in feature_sets:
                feature_sets[feature] = []
            feature_sets[feature].append(datasets[i])
        cond_ent = sum([(len(p) / data_length) * self.calc_ent(p)
                    for p in feature_sets.values()])
        return cond_ent
    
    # 信息增益
    @staticmethod
    def info_gain(ent, cond_ent):
        return ent - cond_ent
    
    def info_gain_train(self, datasets):
        count = len(datasets[0]) - 1
        ent = self.calc_ent(datasets)
        best_feature = []
        for c in range(count):
            c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))
            best_feature.append((c, c_info_gain))
        # 比较大小
        best_ = max(best_feature, key=lambda x: x[-1])
        return best_
    
    def train(self, train_data):
        """
        input:数据集D(DataFrame格式)，特征集A，阈值eta
        output:决策树T
        """
        _, y_train, features = train_data.iloc[:, :
                                                -1], train_data.iloc[:,
                                                                    -1], train_data.columns[:
                                                                                           -1]
        # 1,若D中实例属于同一类Ck，则T为单节点树，并将类Ck作为结点的类标记，返回T
        if len(y_train.value_counts()) == 1:
            return Node(root=True, label=y_train.iloc[0])
        # 2, 若A为空，则T为单节点树，将D中实例树最大的类Ck作为该节点的类标记，返回T
        if len(features) == 0:
            return Node(
                root=True,
                label=y_train.value_counts().sort_values(
                    ascending=False).index[0])

        # 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征
        max_feature, max_info_gain = self.info_gain_train(np.array(train_data))
        max_feature_name = features[max_feature]

        # 4,Ag的信息增益小于阈值eta,则置T为单节点树，并将D中是实例数最大的类Ck作为该节点的类标记，返
        if max_info_gain < self.epsilon:
            return Node(
                root=True,
                label=y_train.value_counts().sort_values(
                    ascending=False).index[0])
        # 5,构建Ag子集
        node_tree = Node(
            root=False, feature_name=max_feature_name, feature=max_feature)

        feature_list = train_data[max_feature_name].value_counts().index
        for f in feature_list:
            sub_train_df = train_data.loc[train_data[max_feature_name] ==
                                        f].drop([max_feature_name], axis=1)

            # 6, 递归生成树
            sub_tree = self.train(sub_train_df)
            node_tree.add_node(f, sub_tree)
        # pprint.pprint(node_tree.tree)
        return node_tree

    def fit(self, train_data):
        self._tree = self.train(train_data)
        return self._tree
    def predict(self, X_test):
        return self._tree.predict(X_test)

In [9]:

datasets, labels = create_data()
data_df = pd.DataFrame(datasets, columns=labels)
dt = DTree()
tree = dt.fit(data_df)

In [10]:

tree

In [11]:

dt.predict(['老年', '否', '否', '一般'])
scikit-learn实例

In [12]:

# data
def create_data():
  iris = load_iris()
  df = pd.DataFrame(iris.data, columns=iris.feature_names)
  df['label'] = iris.target
  df.columns = [
    'sepal length', 'sepal width', 'petal length', 'petal width', 'label'
  ]
  data = np.array(df.iloc[:100, [0, 1, -1]])
  # print(data)
  return data[:, :2], data[:, -1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

In [13]:

from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
import graphviz

In [14]:

clf = DecisionTreeClassifier()
clf.fit(X_train, y_train,)

Out[14]:

DecisionTreeClassifier()

In [15]:

clf.score(X_test, y_test)

Out[15]:

0.9666666666666667

In [16]:

tree_pic = export_graphviz(clf, out_file="mytree.pdf")
with open('mytree.pdf') as f:
  dot_graph = f.read()

In [17]:

graphviz.Source(dot_graph)

Out[17]:

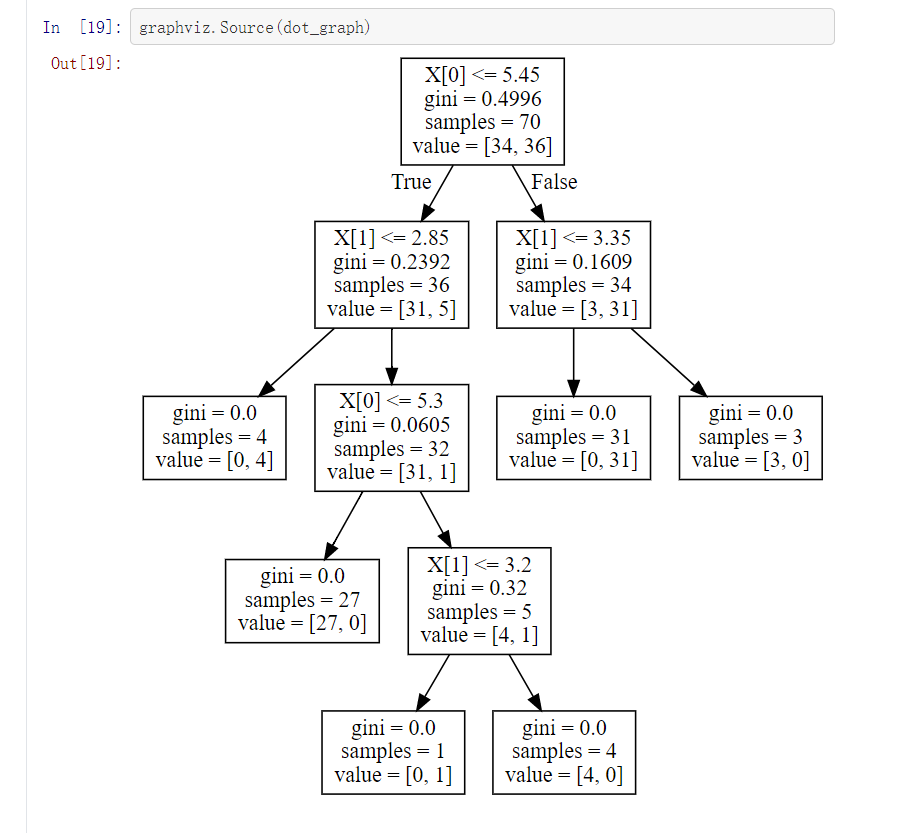
五、实验小结
1、讨论ID3、C4.5算法的应用场景
ID3算法应用场景：
它的基础理论清晰，算法比较简单，学习能力较强，适于处理大规模的学习问题，是数据挖掘和知识发现领域中的一个很好的范例，为后来各学者提出优化算法奠定了理论基础。ID3算法特别在机器学习、知识发现和数据挖掘等领域得到了极大发展。

C4.5算法应用场景：
C4.5算法具有条理清晰，能处理连续型属性，防止过拟合，准确率较高和适用范围广等优点，是一个很有实用价值的决策树算法，可以用来分类，也可以用来回归。C4.5算法在机器学习、知识发现、金融分析、遥感影像分类、生产制造、分子生物学和数据挖掘等领域得到广泛应用。

2、分析决策树剪枝策略
剪枝的目的在于：缓解决策树的"过拟合"，降低模型复杂度，提高模型整体的学习效率
(决策树生成学习局部的模型，而决策树剪枝学习整体的模型)
基本策略：
预剪枝：是指在决策树生成过程中，对每一个结点在划分前进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶子结点。
优点：降低了过拟合地风险，并显著减少了决策树地训练时间开销和测试时间开销。
缺点：有些分支地当前划分虽不能提升泛化性能、甚至可能导致泛化性能下降，但是在其基础上进行地后续划分却可能导致性能显著提高；
预剪枝基于'贪心'本质禁止这些分支展开，给预剪枝决策树带来了欠拟合的风险。
后剪枝：先从训练集生成一棵完整的决策树，然后自底向上地对非叶子结点进行考察，若将该结点对应地子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。
优点：一般情况下后剪枝决策树的欠拟合风险很小，泛化性能往往优于预剪枝决策树。
缺点：自底向上的注意考察，时间开销较高。