图论——支配集

支配集

定义

　　设图G=<V,E>是简单无向图，S⊆V,S≠∅，若对于∀x∈V-S，x都与S里至少一个顶点相邻，则称S是图G的支配集(dominating set)。S是图G的支配集，若S的任何真子集都不是支配集，则称S为图G的极小支配集(minimal dominating set)。S是图G的支配集，若不存在任何其它支配集S'，使得|S'|＜|S|，则称S是图G的最小支配集(smallest dominating set)。若S是图G的最小支配集，则称|S|为图G的支配数(dominating number)，记作γ(G)。

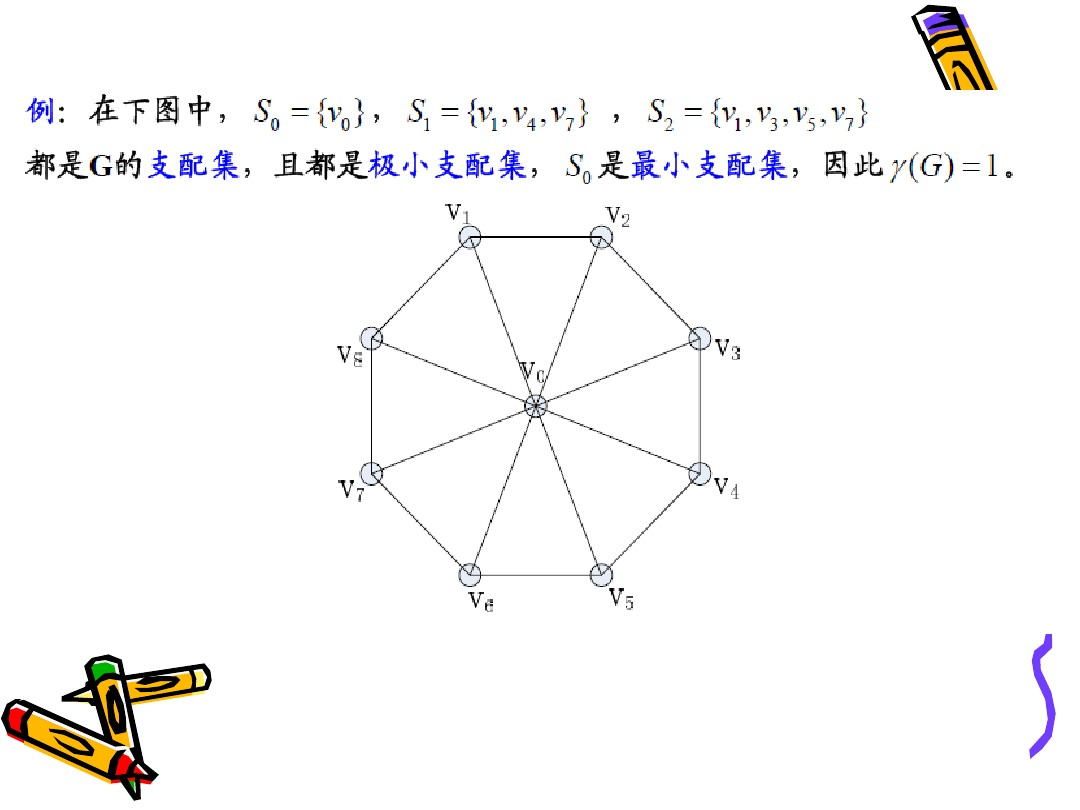
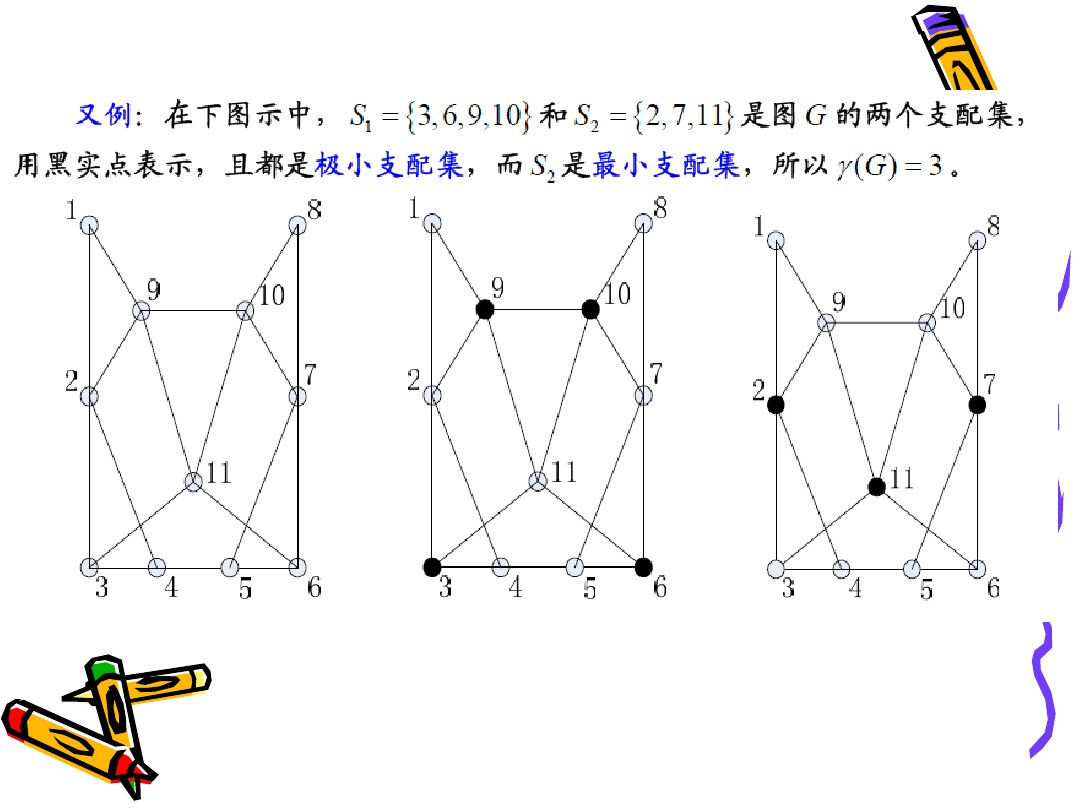
注意

• 最小支配集必是极小支配集，反之不然
• 任一支配集必含有一个极小支配集
• 极小支配集不唯一，最小支配集一般也不唯一
• 对于二部图G(X,Y)，X和Y都是支配集

支配集的几个性质定理

注意：不是每个支配集都是独立集；也不是每个最小支配集都是独立集。

 参考文献：

https://wenku.baidu.com/view/2fc21e476ad97f192279168884868762cbaebb79.html