递归(recursion):程序调用自身的编程技巧。
递归满足2个条件:
1)有反复执行的过程(调用自身)
2)有跳出反复执行过程的条件(递归出口)
递归例子:
(1)阶乘
n! = n * (n-1) * (n-2) * ...* 1(n>0)
//阶乘
int recursive(int i)
{
int sum = 0;
if (0 == i)
return (1);
else
sum = i * recursive(i-1);
return sum;
}
(2)河内塔问题
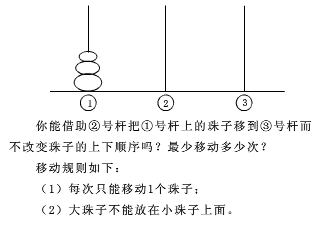
//河内塔
void hanoi(int n,int p1,int p2,int p3)
{
if(1==n)
cout<<"盘子从"<<p1<<"移到"<<p3<<endl;
else
{
hanoi(n-1,p1,p3,p2);
cout<<"盘子从"<<p1<<"移到"<<p3<<endl;
hanoi(n-1,p2,p1,p3);
}
}
(3)全排列
从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。
如1,2,3三个元素的全排列为:
1,2,3
1,3,2
2,1,3
2,3,1
3,1,2
3,2,1
//全排列
inline void Swap(int &a,int &b)
{
int temp=a;
a=b;
b=temp;
}
void Perm(int list[],int k,int m)
{
if (k == m-1)
{
for(int i=0;i<m;i++)
{
printf("%d",list[i]);
}
printf("n");
}
else
{
for(int i=k;i<m;i++)
{
Swap(list[k],list[i]);
Perm(list,k+1,m);
Swap(list[k],list[i]);
}
}
}
(4)斐波那契数列
斐波纳契数列,又称黄金分割数列,指的是这样一个数列:1、1、2、3、5、8、13、21、……
这个数列从第三项开始,每一项都等于前两项之和。
有趣的兔子问题:

一般而言,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔子都不死,那么一年以后可以繁殖多少对兔子?
分析如下:
第一个月小兔子没有繁殖能力,所以还是一对;
两个月后,生下一对小兔子,总数共有两对;
三个月以后,老兔子又生下一对,因为小兔子还没有繁殖能力,总数共是三对;
……
依次类推可以列出下表:

//斐波那契
long Fib(int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
if (n > 1)
return Fib(n-1) + Fib(n-2);
}
转载:http://www.cnblogs.com/joinclear/archive/2013/02/06/2908247.html