【机器学习】周末，我吊死在一颗树上---DoubleArrayTrie

平时使用双数组字典树的场景蛮多的，但是一直没有明白它的构建过程，所以通过各位大佬的文章，总结出自己可以理解的双数组字典树的构建过程，结合一些实际的例子，体会一下具体的用法。
整个文章的思路都是以Trie为基础，然后根据下面几种Trie依次简单梳理一下。

graph LR A[Array Trie] --> B[List Trie] B --> C[Hash Trie] C --> D[Double Array Trie]

在看双数组字典数之前我们先看看什么是字典树。

字典树(Trie)

字典树的定义

字典树：又称为Trie树，前缀树，这是一种字符串上的树形数据结构。
也就是将一个字符串构建成一个树的形状，如下图。
对于有限集合 { AC，ACE，ACFF，AD，CD，CF，ZQ }。
R表示根节点。
对于字符串的处理，我们通常有应用就是在字符串集合中判断字符串是否存在，这个也是匹配算法的一个瓶颈，那么对于普通匹配算法，如果遍历查找时间复杂度是O(n^2)，用二分查找法时间复杂度是O(logn)，如果用TreeMap去匹配，时间复杂度是O(logn)，这里的n指的是词典的大小，如果用HashMap的话，时间复杂度是O(1)，但是空间复杂度又上去了，所以，想要找到一种速度又快，同时内存又省的数据结构，来完成这个匹配操作。字典树就符合这些特征。
先简单了解一下字典树的基本原理

字典树的原理

字典树的每一个边都对应一个字，从根节点往下的路径构成一个个字符串。字典树并不直接在节点存储字符串，而是将词语视作根节点到某一节点之间的一条路径。
并且在终点节点上做个标记（该节点对应词语的结尾），字符串就是一条路径，要查询某一个单词，就需要顺着这条路径从根节点往下走，如果能走到特殊标记的节点（蓝色结点），那么说明当前字符串在集合中，否则当前字符串不在集合中。
下图中是以下词{“abc”、“abcd”、“adb”、“b”、“bcd”、“efg”、“hik”}，构成的前缀树。
原图出自

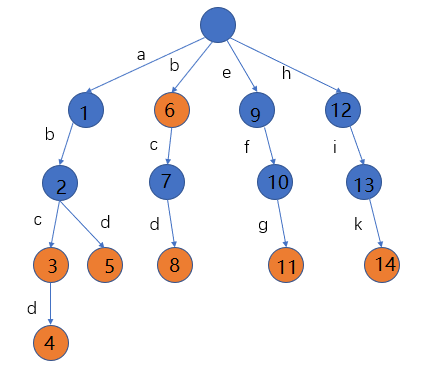
橙色标记该节点是一个词的结尾（词的结尾不一定是到叶子节点），数字只是一个编号，这些词和对应的路径如下表所示。

词语	路径
abc	0-1-2-3
abcd	0-1-2-3-4
adb	0-1-2-5
b	0-6
bcd	0-6-7-8
efg	0-9-10-11
hik	0-12-13-14

备注：橙色=色节点不一定是叶子节点，也就是词的结尾不一定是叶子节点。
字典树的时间复杂度最坏的情况是O(logn)，但是它的速度优于二分查找，毕竟随着路径的深入，前缀匹配是递进的过程，算法不必在比较字符串的前缀。

字典树的特性

1. 以空间换时间
2. 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
3. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
4. 每个节点的所有子节点包含的字符都不相同。

再简单的理解

比如现在有10000个单词列表，我们要判断student这个单词有没有出现过，遍历查找时间复杂度是O(n^2)，用二分查找法时间复杂度是O(logn)，用字典树也是O(logn)，但是上面说了为什么字典树更加优秀，那么用字典树的查找规则就是先找到s，再去s的子树中找t，依次类推，看看能不能找到student这条路径。

字典树的实现

具体需要实现方法有以下几个

• void insert(String word)：添加word；
• void delete(String word)：删除word；
• boolean search(String word)：查询word是否在字典树中；

/**
 * 前缀树
 */
public class TrieTree {
    //字典树节点
    class TrieNode {
        public int path;
        public int end;
        public HashMap<Character, TrieNode> map;

        public TrieNode() {
            path = 0;
            end = 0;
            map = new HashMap<>();
        }
    }

    private TrieNode root;

    public TrieTree() {
        root = new TrieNode();
    }

    /**
     * 插入一个新的单词
     * @param word
     */
    public void insert(String word) {
        if (word == null)
            return;
        TrieNode node = root;
        node.path++;
        char[] words = word.toCharArray();
        for (int i = 0; i < words.length; i++) {
            if (node.map.get(words[i]) == null) {
                node.map.put(words[i], new TrieNode());
            }
            node = node.map.get(words[i]);
            node.path++;
        }
        node.end++;
    }

    public boolean search(String word) {
        if (word == null)
            return false;
        TrieNode node = root;
        char[] words = word.toCharArray();
        for (int i = 0; i < words.length; i++) {
            if (node.map.get(words[i]) == null)
                return false;
            node = node.map.get(words[i]);
        }
        return node.end > 0;
    }

    public void delete(String word) {
        if (search(word)) {
            char[] words = word.toCharArray();
            TrieNode node = root;
            node.path--;
            for (int i = 0; i < words.length; i++) {
                if (--node.map.get(words[i]).path == 0) {
                    node.map.remove(words[i]);
                    return;
                }
                node = node.map.get(words[i]);
            }//for
            node.end--;
        }//if
    }

    public int prefixNumber(String pre) {
        if (pre == null)
            return 0;
        TrieNode node = root;
        char[] pres = pre.toCharArray();
        for (int i = 0; i < pres.length; i++) {
            if (node.map.get(pres[i]) == null)
                return 0;
            node = node.map.get(pres[i]);
        }
        return node.path;
    }

    public static void main(String[] args) {
        TrieTree trie = new TrieTree();
        System.out.println(trie.search("程龙颖"));//f
        trie.insert("自然人");
        trie.insert("自然");
        trie.insert("自然语言");
        trie.insert("自语");
        trie.insert("入门");
        System.out.println(trie.search("自然"));//t
        trie.delete("自然语言");
        System.out.println(trie.search("自然语言"));//f
        trie.insert("自然语言");
        System.out.println(trie.search("自然语言"));//t
        System.out.println(trie.prefixNumber("自然"));//3
    }
}

DFA简单理解

TrieTree本质上是一个确定有限自动机（DFA)。
DFA的特征：有一个有限状态集合和一些从一个状态通向另一个状态的边，每条边上标记有一个符号，其中一个状态是初态，某些状态是终态。但不同于不确定的有限自动机，DFA中不会有从同一状态出发的两条边标志有相同的符号。
对于DFA来说，每个节点代表一个“状态”，每条边代表一个“变量”。

双数组字典树

双数组字典树（DoubleArrayTrie, DAT）是由三个日本人提出的一种字典树的高效实现，兼顾了查询效率与空间存储。DAT极大地节省了内存占用。

优点

在Trie数实现过程中，我们发现了每个节点均需要 一个数组来存储next节点，非常占用存储空间，空间复杂度大，双数组Trie树正是解决这个问题的。双数组字典树(DoubleArrayTrie)是一种空间复杂度低的Trie树，应用于字典树压缩、分词、敏感词等领域。所以，DAT是前缀树的一个变形，同样也是一个DFA。

缺点

每个状态都依赖于其他状态，所以当在词典中插入或删除词语的时候，往往需要对双数组结构进行全局调整，从而灵活性能较差。

定义

将原来需要多个数组才能表示的Trie树，使用两个数组就可以存储下来，可以极大的减小空间复杂度。由于用base和check两个数组构成，又称为双数组字典树。
具体来说就是使用两个数组base[]和check[]来维护Trie树，base[]负责记录状态，check[]用于检验状态转移的正确性，当check[i]为负值时，表示此状态为字符串的结束。
具体来说，当状态b接受字符c然后转移到状态p的时候，满足的状态转移公式如下：

p = base[b] + c
check[p] = base[c]	

构建双数组的过程

对于词典 { AC，ACE，ACFF，AD，CD，CF，ZQ }，构建双数组具体过程如下。
在构造之前，先梳理几个概念

• STATE：状态，也就是数组的下标
• CODE： 状态转移值，实际为字符的 ASCII码
• BASE： 表示后继节点的基地址的数组，叶子节点没有后继，标识为字符序列的结尾标志

主要是基于 dart-java，此版本对双数组算法做了一个改进，即darts双数组中有以下的改进。

	base[0] = 1 
	check[0] = 0

第二个改进就是令字符的code = ascii+1

结合两个数组的状态转移公式有以下条件

base[0] = 1 
check[0] = 0 
p = base[b] + c
check[p] = base[c]	

基于base和check两个数据构建双数组的流程整体如下

1 建立根节点root,令base[root] =1
2 找出root的子节点 集{root.childreni }(i = 1...n) , 使得 check[root.childreni ] = base[root] = 1
3 对 each element in  root.children : 
　　1）找到{elemenet.childreni }(i = 1...n) ，注意若一个字符位于字符序列的结尾，则其孩子节点包括一个空节点，其code值设置为0找到一个值begin使得每一个check[ begini + element.childreni .code] = 0
　　2）设置base[element.childreni] = begini
　　3）对element.childreni 递归执行步骤3，若遍历到某个element，其没有children，即叶节点，则设置base[element]为负值（一般为在字典中的index取负）

备注：构建的时候，从广度搜索，从深度构建词典
1、根据上面的那个例子{ AC,ACE,ACFF,AD,CD,CF,ZQ }来说，最开始有

base[0] = 1 
check[0] = 0 

备注：ascii表格

	65 	A
	66 	B
	...

此外，结合darts双数组的改进code= ascii+1, 以及i = base[0] + code可以得到下面每个字符的position(i)和对应字符的code值。base[0] = 1。

	root	A	C	D	E	F	Q	Z
i	0	67	69					92
code	0	66	68	69	70	71	82	91

2、根据构造过程中的第二步，距离root节点深度为1的所有children其check[root.childreni] = base[root] = 1，在模式串中root的三个子节点'A', 'C', 'E'的check值都是1， 假设root经过A C Z 的作用分别到达(p_1 , p_2, p_3)三个状态，可以得到下面矩阵。

	root	A	C	Z
i	0	67	69	92
base	1
check	0	1	1	1
state	p0	p1	p2	p3

3、根据构建的第三步，状态p1是由条件 'A'触发的，那么'A'的base值的计算方式需要满足以下的规则：
我们知道，对于每一个字符， 需要确定一个base值，使得对于所有以该字开头的词，在双数组中都能放下。
已知A的子节点值为{C D}， 需要找一个begin值，使得check[begin +'C'.code] = check[begin +'D'.code] = 0满足， 即check[begin + 68] = check[begin + 69] = 0，换句话说，需要找到一个begin，从而找到之前没有使用过的空间。

a、当begin=1的时候，有check[1+ 68] 和check[1+ 69] 都必须为0，
但是check[1 + 68] 存在字符‘C’，
所以check[begin +’C'.code] = check[begin +’D’.code] = 0不成立。
b、当begin=2的时候
需要有check[2+ 68] 和check[2 + 69] 的值都必须为0
有check[begin + 68] = check[begin + 69] = 0
所以有base[p1] = begin = 2， 状态p1= 67。

p4 = base[p1] + 'C'.code = 2 + 68 = 70 ,
p5 = base[p1] + 'D'.code = 2 + 69 = 71，
check[p5] = check[p4] = base[p1] = 2,
那么有以下矩阵
备注：AC指的就是A左子树C，AD指的就是A的右子树D。

| | root| A| C | Z|AC|AD|
|--|--|--|--|--|--|--|--|
|i| 0 | 67| 69 | 92 |70|71|
|base| 1 | 2| | ||
|check| 0 | 1| 1| 1| 2|2|
|state| p0 | p1| p2| p3|p4|p5|

4、根据上一步，继续深度遍历，走A的左子树C，继续推导。已知C的子节点是{null、E、F}，需要找一个begin值，使得check[begin +null.code] = check[begin +'E'.code] = check[begin +'F'.code] = 0满足， 在子节点有空的情况下，需要设置base[null] = -1（取负整数，从-1开始，下一次出现就是-2）。
所以有base[null] = -1
所以就有(p_{null}) = check[null] = p4 + 2，因为position为70，71有占位。所以后移。
所以就有(p_{null}) = 72
同时出现空的时候，有check[null] = (p_{null}) = 72
又因为check[null] = base[p4]
所以base[p4] = 72
null由*表示

	root	A	C	Z	AC	AD	AC*	ACE	ACF
i	0	67	69	92	70	71	72
base	1	2			72		-1
check	0	1	1	1	2	2	72
state	p0	p1	p2	p3	p4	p5	p6=null	p7	p8

5、然后继续求ACE和ACF这两个条链路，先求base[p7]和base[p8]。
有公式：check[begin + 'E'.code] = 0
有公式：check[begin + 'F'.code] = 0
现在当begin从3开始，当为3的时候，
check[3 + 70] = 0成立
check[3 + 71] = 0成立
所以
p7 = base[p4] + E.code = 72 +70 = 142
p8 = base[p4] + F.code = 72 +71 = 143
所以
check[p7] = base[p4] = 72
check[p8] = base[p4] = 72

| | root| A| C | Z|AC|AD|AC*|ACE|ACF|
|--|--|--|--|--|--|--|--|--|--|--|
|i| 0 | 67| 69 | 92 |70|71|72|142|143|
|base| 1 | 2| | |72||-1||
|check| 0 | 1| 1| 1| 2|2|72|72|72|
|state| p0 | p1| p2| p3|p4|p5|p6=null|p7|p8|

6、然后开始算ACE*这个链路，由于自己诶单包含为null节点，所以有
base[null] = -2
所以就可以有(p_{null}) = check[null] =73，因为position为70，71有占位。所以后移，给一个空的值就行。
所以就有(p_{null}) = 73
同时出现空的时候，有check[null] = (p_{null}) = 73
又因为check[null] = base[p7]
所以base[p7] = 73

| | root| A| C | Z|AC|AD|AC|ACE|ACF|ACE|
|--|--|--|--|--|--|--|--|--|--|--|--|
|i| 0 | 67| 69 | 92 |70|71|72|142|143|73|
|base| 1 | 2| | |72||-1|73|-2|
|check| 0 | 1| 1| 1| 2|2|72|72|72|73|
|state| p0 | p1| p2| p3|p4|p5|p6=null|p7|p8|p9=null|

7、然后走ACFF，ACFF*。依次类推。

最终的不含非空节点矩阵如下

	root	A	C	Z	C	D	D	F	Q	E	F	F
i	0	67	69	92	70	71	77	79	86	142	143	74
base	1	2	8	4	72	76	78	80	83	73	3	75
check	0	1	1	1	1	2	2	8	8	4	72	72
state	p0	p1	p2	p3	p4	p5	p6	p7	p8	p9	p10	p11

使用DFA的形式来描绘，节点表示state，字符作为转移条件，不同字符触发不同的state，可得到到树如下图，其中红色部分正好是第5步骤的矩阵；绿色部分是按照模式集合得到的ouput表。

参考

https://blog.csdn.net/u013300579/article/details/78869742

https://blog.csdn.net/zhoubl668/article/details/6957830

https://github.com/komiya-atsushi/darts-java

https://linux.thai.net/~thep/datrie/datrie.html

https://www.cnblogs.com/ooon/p/4883159.html

https://blog.csdn.net/xlxxcc/article/details/67631988