[ 具体数学 ] 1:递归式与封闭式

递归问题

汉诺塔(HANOI)

命题

有三根杆子，第一根有大小从小到大共\(n\)个盘子，要求遵循以下3个规则，将在第一个杆子上全部的盘子移至第三个杆子。

1. 每次只能移动一个盘子。
2. 每次只能移动每个杆子最上面的盘子。
3. 每根杆子上的盘子下面大，上面小。

求问题的最小步数。

例子:

当\(n=3\)时，移动方法如下图所示。

最小移动次数为\(7\)，故\(n=3\)时命题的解为\(7\)。

解决

方法：命名并求解

命名

1. 设\(H(n)\)为\(n\)个盘子时汉诺塔问题的解.
2. 三个杆子的编号分别为\(A,B,C\).
3. 第\(i\)层盘子为\(h_i\).

注: 书上或有的博文上用\(H_n\),但笔者认为用\(H(n)\)更为合适,因为问题的解更像函数.

求解

显然,\(H(1)=1\)

观察可得,将\(n\)个盘子从\(A\)移动到\(B\)相当于将\(h_1,h_2\cdots h_{n-1}\)移动至\(B\)后,将\(h_n\)移至\(C\),再将\(h_1,h_2\cdots h_{n-1}\)移至\(C\).

由定义知,将\(h_1,h_2\cdots h_{n-1}\)从\(A\)移至\(B\)需\(H(n-1)\)步.

\(\therefore H(n)=2H(n-1)+1\qquad H(1)=1\)

检验

已知\(H(3)=7\)

\[\because H(n)=2H(n-1)+1 \]

\[\therefore H(3)=2\times H(2)+1 \]

\[\therefore H(3)=2\times (2\times H(1) + 1) + 1 \]

\[\therefore H(3)=2\times (2\times 1+1)+1 \]

\[\therefore H(3)=2\times 3+1 \]

\[\therefore H(3)=7 \]

代码

# python
A = [3, 2, 1]
B = []
C = []

def move(n, source, target, auxiliary):
    if n > 0:
        # Move n - 1 disks from source to auxiliary, so they are out of the way
        move(n - 1, source, auxiliary, target)

        # Move the nth disk from source to target
        target.append(source.pop())

        # Display our progress
        print(A, B, C, '##############', sep='\n')

        # Move the n - 1 disks that we left on auxiliary onto target
        move(n - 1, auxiliary, target, source)

# Initiate call from source A to target C with auxiliary B
move(3, A, C, B)

递归式

递归是在计算过程中调用自己的求解方法。

构成递归需具备的条件

1. 子问题须与原始问题为同样的问题，且更为简单。

2. 不能无限制地调用本身，须有边界，化简为非递归状况处理。

汉诺塔的求解公式就是典型的递归。

封闭式

在前面的递归式中，不难看出，计算\(H(n)\)需要进行\(n-1\)次将\(H(n)\)替换为\(2H(n-1)+1\)的操作。

所以递归式虽然直观，但不方便计算。

封闭式可以直接计算出函数的值，不需要进行递归。

我们尝试将汉诺塔的递归式转换为封闭式。

法1

求解

\[\because H(n)=2H(n-1)+1 \]

\[\therefore H(n)=4H(n-2)+3 \]

\[\therefore H(n)=8H(n-3)+7 \]

\[\vdots \]

\[\therefore H(n)=2^{n-1}H(1)+2^{n-1}-1 \]

\[\therefore H(n)=2^{n-1}+2^{n-1}-1 \]

\[\therefore H(n)=2^n-1 \]

检验

已知\(H(3)=7\)

\[\because H(n)=2^n-1 \]

\[\therefore H(3)=2^3-1 \]

\[\therefore H(3)=7 \]

法2

求解

\[\because H(n)=2H(n-1) \]

\[猜想: \]

\[H(n)=2^n-1 \]

\[证明: \]

\[I. 当n=1时,显然成立 \]

\[II. 假设n=k时成立,即H(k)=2^k-1,则: \]

\[\because H(n)=2H(n-1)+1 \]

\[\therefore H(n+1)=2H(n)+1 \]

\[\because H(n)=2^k-1 \]

\[\therefore H(n+1)=2\cdot (2^k-1)-1 \]

\[\therefore H(n+1)=2^{k+1}-2+1 \]

\[\therefore H(n+1)=2^{k+1}-1 \]

证毕.

平面上的直线(LINE)

命题

在一个平面内,\(n\)条直线最多能把平面分成多少个区域

解决

方法:命名并求解

命名

1. 设\(L(n)\)为\(n\)条直线把平面分成的最大区域数.

求解

显然,\(L(1)=2\)

之后每一条直线都能与之前每一条直线有一个交点.

于是能产生\(n\)个新平面.

如下图

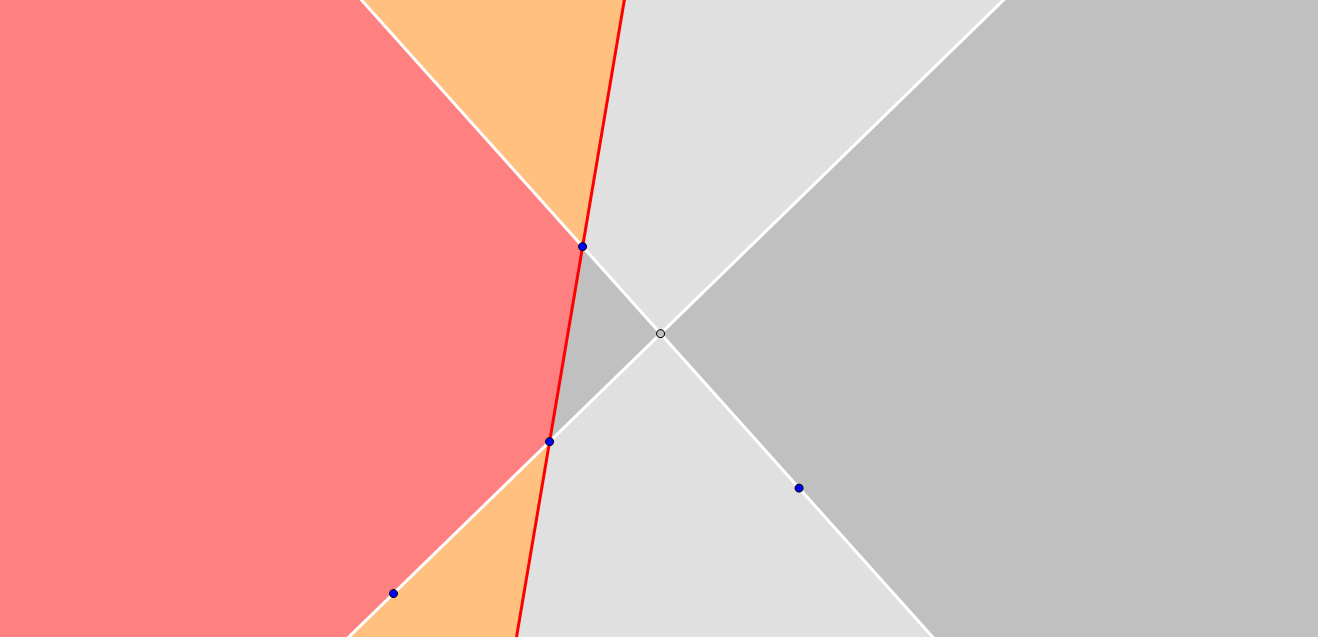
白线 : 原有的线

灰面 : 原有的面

红线 : 新增的线

红面,橙面 : 新增的面

综上:$$L(n) = L(n-1) + n$$

转为封闭式

求解

\[\because L(n)=L(n-1)+n\qquad L(1)=2 \]

\[\therefore L(n)=L(n-2)+(n-1)+n \]

\[\therefore L(n) = L(n-3)+(n-2)+(n-1)+n \]

\[\vdots \]

\[\therefore L(n) = L(1) + 2 + 3 + \cdots + (n-1) + n \]

\[\therefore L(n) = 2+\sum_{i=2}^{n}i \]

如何将和式转为递归式呢?
见下一章:

[ 具体数学 ] 和式与封闭式