(Global Round1)题解(1110A~F)
(zhanglichen 2021.1.2)
(A.Parity)
给出(2)个数字(b,k)。
给出一个长度为(k)的数组,询问(sum_{i=1}^na_i*b^{k-i})的奇偶性。
(Solution)
简单模拟,(C)语言月考。
(B.Tape)
给出以根长度为(m)的木棍,上面有(n)个断点。你可以截取(k)个任意长度的碎片把端点接起来。对于一个长度为(x)的碎片,如果把它放在位置(p),那么它会覆盖(p)到(p+x-1)位置的所有端点。询问碎片的最小总长度。
(Solution)
建一个断点的差分数组,从大到小排序,然后贪心的取前(k-1)个差分元素空出来即可。
(C.Meaningless Operation)
给出一个范围是([0,2^{25}-1])的正整数(a),请你找到(1)个正整数(b(0<b<a)),使得(gcd(aoplus b,a&b))的值最大。
(Solution)
首先提取出(a)的二进制形式。
如果存在一个(0)位,比如(111101111),那么我们可以把(b)设为(000010000),答案是(111111111),显然这是最优解。
现在考虑不存在(0)位的情况。由于(a)不存在(0)位,我们要求的值可以转化为(gcd(b,a-b))。答案就是(a)的最大因数。
(D.Jongmah)
给出以一个数组(a),(1)个三元组((a,b,c))称为合法:
(1)(a=b)且(b=c)。
(2)(a+1=b)且(b+1=c)。即((a,b,c))可以构成一个顺子。
(Solution)
假设我们当前枚举到的元素值为(x),那么它对答案的贡献可以有以下(3)种:
((x,x,x))
((x-2,x-1,x))
((x-1,x,x+1))
((x,x+1,x+2))
考虑一个(dp)的思路。
定义状态(f(i,j,k,l))表示到第(i)个元素为止,第(i)个元素,有(j)个作为第(2)种状态被统计,有(k)个作为第(3)种状态被统计,有(l)个作为第(4)种状态被统计时对答案的贡献。并且只需要统计(j<3)且(k<3)且(l<3)
的情况即可。因为(3)个((x,x+1,x+2))和(x,x+1,x+2)各取三个对答案的贡献是一样的。
状态转移方程:(f(i,j,k,l)=max(f(i-1,?,j,k))+l+(c[i]-j-k)/3)
最后取(max(f(m,i,0,0)))为答案。
(E.Magic Stone)
给出(2)个长度为(n)的数组(c)和(t),一次操作可以把(c_i=c_{i+1}+c_{i-1}-c_i),同时保证位置(i+1)和位置(i-1)合法。
询问是否可以通过一些操作把(c)变成(t)。
(Solution)
性质:不停的做这个操作,只是把差分数组打乱。
所以建立(c)和(t)的差分数组并排序,询问是否一样即可。前提要保证(c_1)等于(t_1),(c_n)等于(t_n)。
(F.Nearest Leaf)
给出一棵带边权的树,请你根据以下代码给每个节点重新编号:
next_id = 1
id = array of length n filled with -1
visited = array of length n filled with false
function dfs(v):
visited[v] = true
id[v] = next_id
next_id += 1
for to in neighbors of v in increasing order:
if not visited[to]:
dfs(to)
多次询问,每次询问给出三个数(v,l,r),表示询问从节点(v)到节点编号在(l)到(r)之间的叶子节点的最短距离。
(Solution)
根据(DFS)序的性质,一个节点(x)的子树区间是(x)到(x+size[x]-1)。
可以考虑对询问离线,(v)相同的询问一组。
然后先构建出一个数组(d),表示节点(1)到所有叶子节点的距离。然后考虑搜索的时候修改(d)数组并回答询问。
假设当前搜索到的节点是(x),从(x)转移到(x)的儿子(y),(y)的子树区间的所有元素(-1),除了(y)子树区间的所有元素(+1)。这样数组(d)存的就是(y)到所有叶子节点的距离。
回答每个询问,就找(d)上(l)到(r)之间的最小元素。
区间修改+区间询问,显然可以用线段树维护。
神秘(Bug):线段树要开到(n+1),不然会报错,不知道为什么。
(G.Tree-Tac-Toe)
树上有些节点已经被染成白色了。先手可以把树上未染色的节点染成白色,后手可以把树上未染色的节点染成黑色。当有一方把树上一个长度为(3)的路径染成自己的颜色时胜利。
询问在双方都足够聪明的情况下,谁能赢。
(Solution)
为了方便讨论,先把已经被染色的节点转化成未染色的节点。
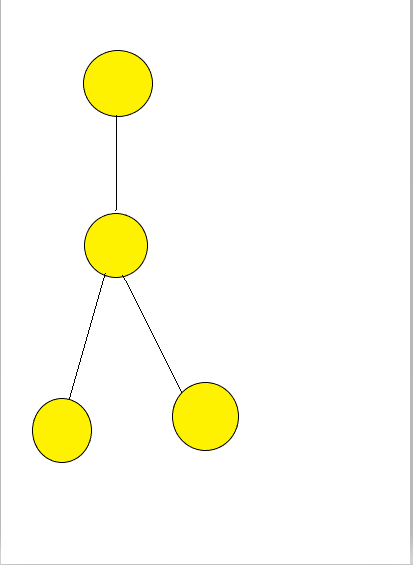
对节点作这样的构造可以实现未染色并且不影响胜负的效果。
如果存在一个度数大于(4)的点,先手必胜。
如果存在一个度数为(3),并且(2)个儿子不是叶子的点,先手必胜。
如果存在(2)个度数为(3),且之间距离是奇数的点,先手必胜。
否则平局。