删除操作
我们按照被删除的节点的子节点个数,分以下三种情况来讨论:
- 被删除节点没有孩子。只需要修改其父节点,用NIL去替换自己。
- 被删除节点有一个孩子。也只需要修改其父节点,用这个孩子去替换自己。
- 被删除节点有两个孩子。那么先找z的后继y(一定在z的右子树中),并让y占据树中z的位置。z的原来的右子树部分称为y的新的右子树,并且z的左子树成为y的左子树。
前两种情况比较简单,至于第三种情况,我们还可以细分:
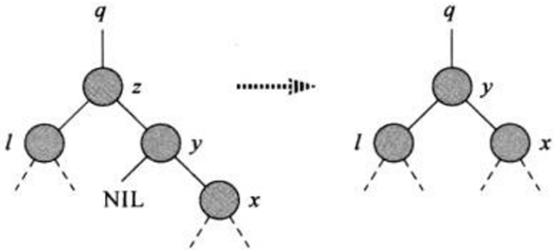
a.如果z的后继y就是z的右孩子(即y没有左孩子),直接用y代替z,并保留y的右子树,如下图所示:
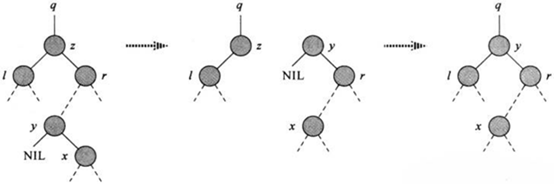
b.如果z的后继y不是z的右孩子,先用y的右孩子替换y,再用y替换z。如下图所示:
算法描述
// 替换 RB_TRANSPLANT(T, u, v) if u.p == T.nil // u是根节点 T.root = v elseif u == u.p.left // u是左孩子 u.p.left = v else // u是右孩子 u.p.right = v v.p = u.p // 更新父节点 备注:强调该替换算法只处理v的父节点,并没有考虑u,v子节点的情况,u,v子节点都需要自行处理 // 查找最小元素 TREE_MINIMUN(X) while x.left != T.nil x = x.left return x // 查找最大元素 TREE_MAXIMUN(X) while x.right != T.nil x = x.right return x // 删除 RB_DELETE(T, z) y = z y-original-color = y.color if z.left == T.nil // 删除节点z没有左孩子,直接用右孩子来替换自己(真.删除) x = z.right // ① RB_TRANSPLANT(T, z, z.right) elseif z.right == T.nil // 删除节点z没有右孩子,直接用左孩子来替换自己(真.删除) x = z.left RB_TRANSPLANT(T, z, z.left) else // 删除节点z存在左孩子和右孩子 y = TREE_MINIMUN(z.right) // y赋值为删除节点z右子树最小节点(此时的y绝对没有左孩子)② y-original-color = y.color // x = y.right // if y.p != z // 右子树最小节点y不是z的孩子 RB_TRANSPLANT(T, y, y.right) // 用y的右孩子替换y本身 ③ else // 说明删除节点z的后继y就是z的右孩子,此时可以保持y的孩子节点,无需变动 RB_TRANSPLANT(T, z, y) // 用y替换掉z节点(y的孩子关系已经处理完成了) y.right = z.right // 处理删除节点z的右孩子关系 y.right.p = y y.left = z.left // 处理删除节点z的右孩子关系 y.left.p = y y.color = z.color // 着色新结点的颜色(假.删除,本质是替换,因此不会影响被替换节点的红黑性质) if y-original-color == BLACK // 删除红色节点不会破坏红黑树的特性 ④ RB_DELETE_FINXUP(T, x) // 删除再平衡
备注:
① x表示的是发生了移动的节点,可能会破坏红黑树的性质
②删除结点用其子树中大于该节点的最小节点(该节点一定不存在左子节点)进行替换,假设用左子节点来替换,那是不可行的,
遍历左孩子只能找到最小节点,如果用左孩子的最小节点来替换被删除的节点,那么就会破坏红黑树特性(根节点一定小于左孩子),
③ 替换操作需要考虑两个元素的孩子关系,因为 y 没有左孩子,因此替换之后,不需要考虑 y 原来的左孩子问题,但是 y 有右孩子,又因为右孩子就是 y.right ,因此无需做任何变动
y会被用来替换z,相当于y也被删除了,需要处理原来y原来的一些孩子关系(真.删除)
④ y-original-color是记录被删除节点的颜色,如果颜色是红色,那么其子节点一定是黑色(被删除的节点都是被自己的子节点所取代),连续2个黑色并不违背红黑树的性质。
如果颜色是黑色,那么子节点的颜色可能是红色,被删除节点的父节点也可能是红色,此时就会破坏红黑树的性质
⑤ 真删除表示节点被真实删除了,新替补上来的节点的颜色并没有被修改,假删除,替换的节点孩子关系被替换,并且颜色也被替换,对原节点亲属关系几乎没有改变
删除再平衡平衡算法描述
// 删除再平衡(心里默念x是双色) RB_DELETE_FINXUP(T, x) while x != T.root and x.color == BLACK // 关于x.color == RED情况说明见① if x == x.p.left // x是父节点左孩子 w = x.p.right // w是父节点右孩子 if w.color == RED // 兄弟节点颜色是红色,说明父节点必须是黑色 w.color = BLACK // case1 x.p.color = RED // case1 LEFT_ROTATE(T, x.p) // case1 注意此时x.p的右孩子已经更新 w = x.p.right // case1 w指向原先自己的左孩子 if w.left.color == BLACK and w.right.color == BLACK // w的孩子节点都是黑色 w.color = RED // case2 修改w节点的颜色为红色 x = x.p // case2 x指向其父节点 elseif w.right.color == BLACK // w的左孩子是红色,右孩子是黑色 w.left.color == BLACK // case3 w.color = RED // case3 RIGHT_ROTATE(T, w) // case3 w = x.p.right // case3 w指向原先自己的左孩子 w.color = x.p.color // case4 w着色为父节点的颜色 x.p.color = BLACK // case4 设置x父节点为黑色 w.right.color = BLACK // case4 设置w右孩子的颜色为黑色 LEFT_ROTATE(T, x.p) // case4 左旋x的父节点 x = T.root // case4 else // same x.color = BLACK // 如果x.color==RED 直接将x的颜色着色为BLACK
备注:
①:为啥不考虑x是红色的情况?
假设被真.删除的节点z是黑色(除非真.删除是根结点外)都将导致原先包含z结点的简单路径上的黑结点数少1,将违背性质3。修正这一问题的方式是我们将现在占据z结点位置的x结点"再涂上一层黑色"(②),当然,涂色操作并不反映在代码上,即我们不会修改x的color属性,我们只是"在心中记住",适当的时候会把x的这层黑色涂到某个红色结点上以达到目的。"涂了两层色"的x结点可能是双层黑色或红黑色,它们分别会"贡献"2或1个黑色结点数。
② 这句话很难理解,意思是现在黑高肯定少了1,那么就需要增加一个黑色节点,既然是x替换了被删除的节点,那么这个黑色就被着色在x上,这样x会有两种颜色(一种他本身自带的颜色,一种黑色,黑色是被删除节点赋予x的),这样可以保证原先包含z结点的简单路径黑高保持不变。
③ 关于当一条路径上一个节点被删除,导致高度下降问题分析
红黑树的高度是以黑高来确认的,我承认事实上树高下降了,但是通过着色黑高并没有下降,黑高的不下降对于未来的插入操作将会变得简单,这也可以说明红黑树并非完全平衡。
④ RB_DELETE-FIXUP修正的目的就是要x路径上黑高+1(因为真删除黑色节点会导致黑高-1)
分析RB_DELETE-FIXUP修正过程
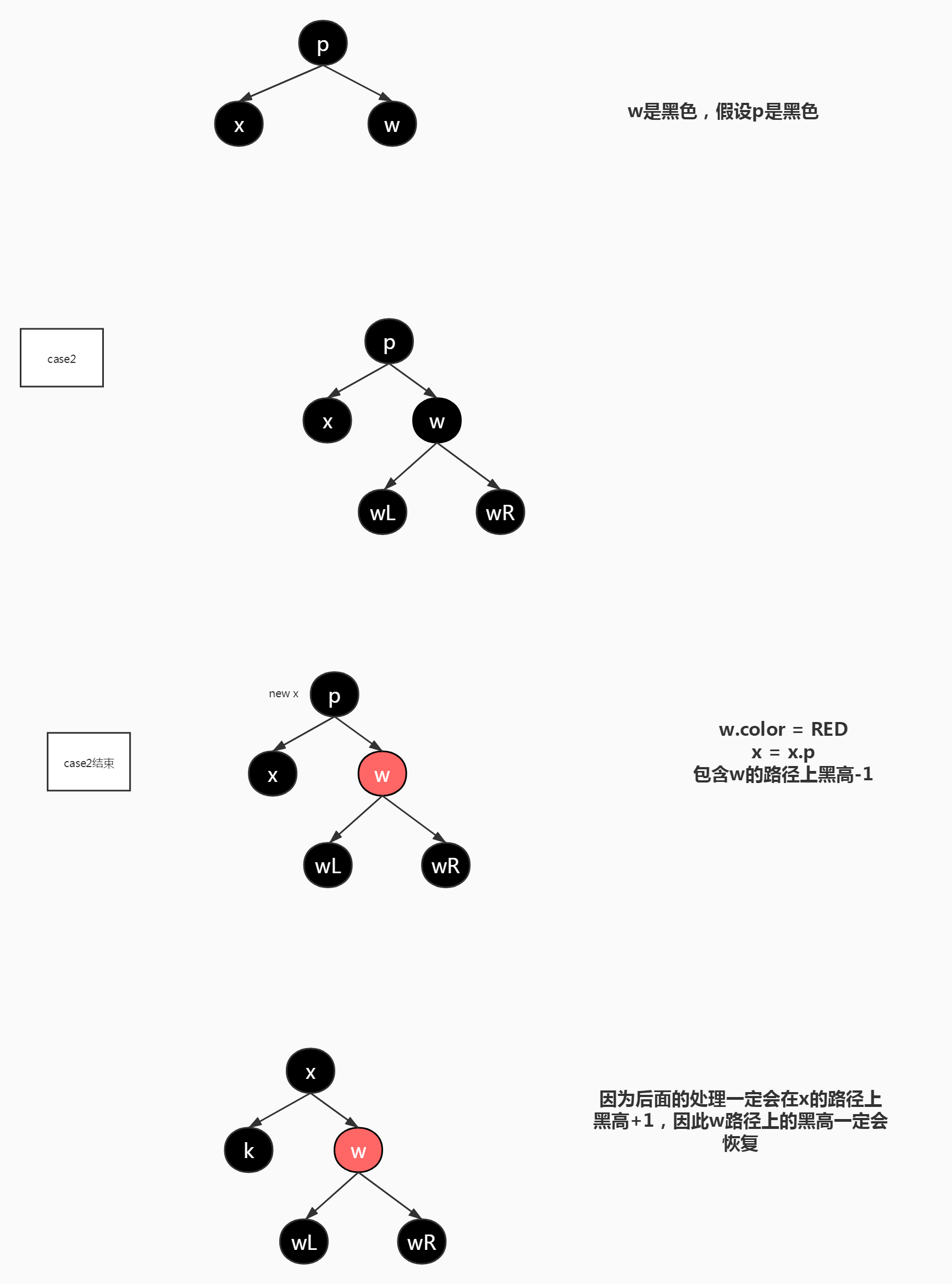
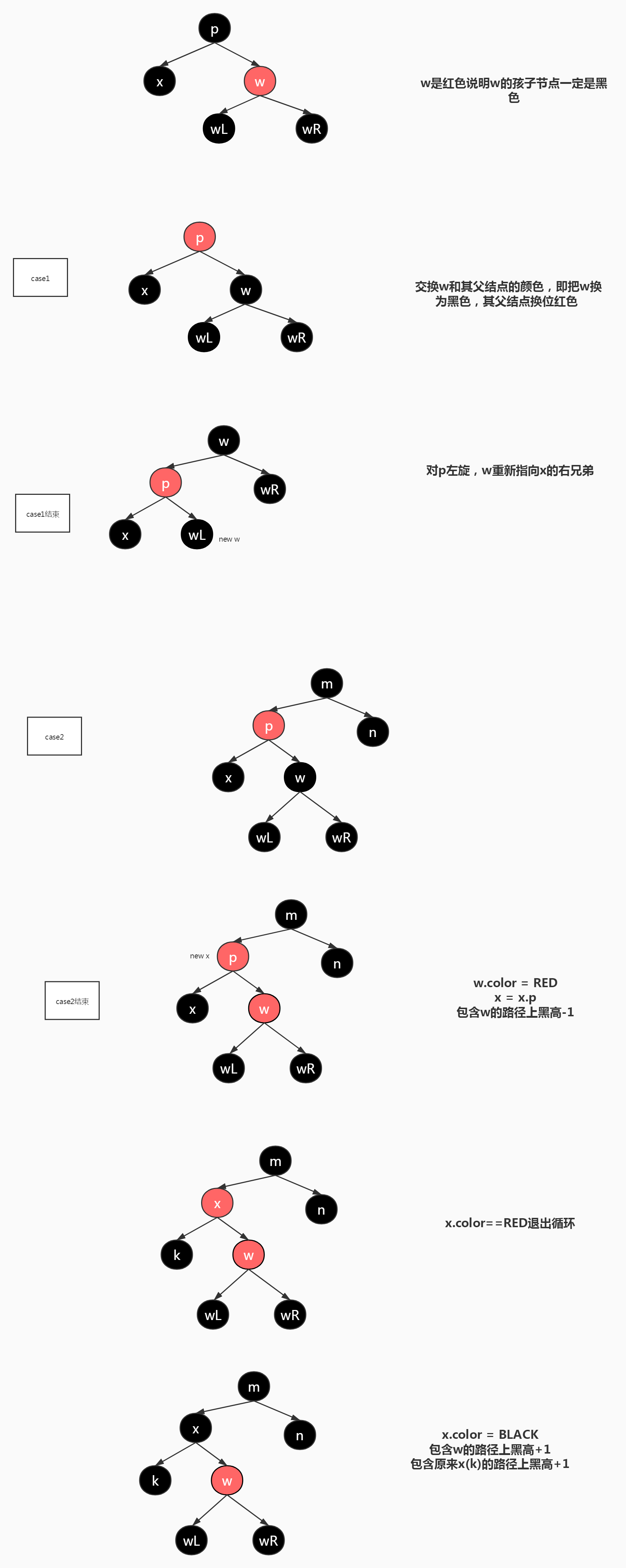
Case 1:x的右兄弟w是红色,说明x的父结点一定是黑色。
所作的操作是:交换w和其父结点的颜色,即把w换为黑色,其父结点换位红色;然后对父结点左旋,w重新指向x的右兄弟(该结点原本是w的左孩子,所以一定为黑色),黑高保持不变。
有什么影响:将x的兄弟节点变成黑色
Case 2:x的兄弟节点w是黑色的,并且w的两个子节点也是黑色的。
所作的操作是:将w换为红色,x指向其父结点,w路径上黑高-1。
有什么影响:将x本身的黑色着色给父节点来实现x路径上黑高+1,并且w路径黑高+1这个目的,这个目的的实现与父节点的颜色密切相关,父节点是红色,那么会退出循环(循环体外实现给父节点着色为黑色的功能),父节点着色黑色实现了黑高+1这个目的,如果父节点为黑色,那么只能x上跳一级继续循环,期待后面可以实现黑高+1这个目的
Case 3:x的兄弟节点w是黑色的,并且w的左孩子为红色,右孩子为黑色。
所作的操作是:着色w的左孩子为黑色,着色w本身为红色,对w进行右旋操作,黑高保持不变。
有什么影响:case3是将w的右孩子变成红色,目的是为了构造case4
Case 4:x的兄弟节点w是黑色的,并且w的右孩子为红色,左孩子颜色任意。
所作的操作是:w着色为父节点的颜色,设置x父节点为黑色,设置w右孩子的颜色为黑色,左旋x的父节点,退出循环。
有什么影响:case4实现了x路径上黑高+1
case说明:
1.case2,case3,case4的w节点一定是黑色,因为case1可以确保这一点
2.观察所有case,发现只有case2和case4可以实现x路径黑高+1这个目的
详细分析流程如下图
/**********case1+case2*******************/
/*********case1+case3+case4************************/

/***********case2***************************/
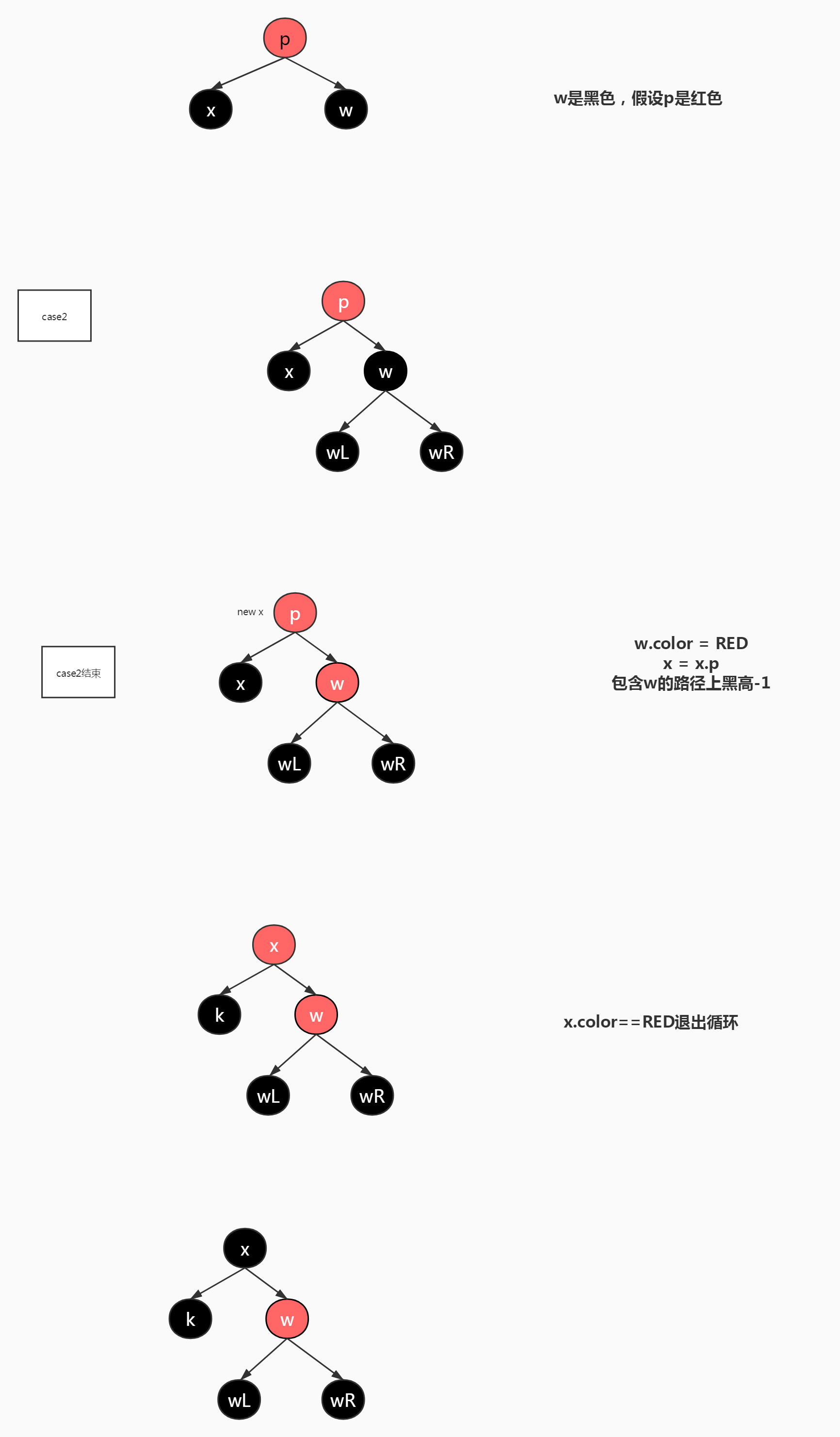
/*******case2*********************/