简介:
对于基本动态集合操作时间复杂度均为O(h)的二叉搜索树。但遗憾的是,只有当二叉搜索树高度较低时,这些集合操作才会较快;
即当树的高度较高(甚至一种极端情况是树变成了1条链)时,这些集合操作并不比在链表上执行的快。于是我们需要构建出一种“平衡”的二叉搜索树。
性质:
与普通二叉搜索树不同的是,红黑树在每个结点上增加了一个存储位来表示该结点的颜色(只能是Black或Red中的一种),
因此此时一个结点包含5个属性:color,key,left,right和p。通过对各个结点的颜色进行约束,
可以保证任何一条从根到叶子的简单路径上不会比其他路径长2倍(这就保证了“平衡”)。
性质一: 根结点和叶结点是黑色的; 性质二: 红色结点的子结点必是黑色的; 性质三: 任何一个结点到其所有后代叶结点的简单路径包含相同数目的黑色结点,并称这个黑色结点的数目(不包含出发结点)为黑高(black-height,用bh(x)表示,
红黑树的黑高为根结点的黑高)。
强调:黑高是非常重要的一个概念,红黑树保持平衡主要就是看黑高
下图是一棵红黑树
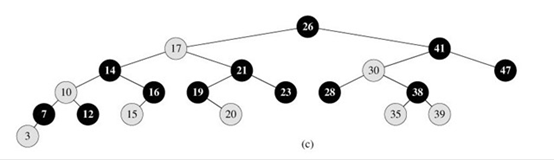
也许你会奇怪上面的红黑树并没有满足叶结点必须是黑色这条性质呀。事实上它是满足的,因为上图画出的其实是树的内部结点,
我们在真正处理时,会把上图中的叶结点的左右孩子指向一个值为NIL,颜色为黑色的结点(外部节点),
即真正的叶结点是这个黑色的值为NIL的结点,这样就满足红黑树性质了。如下图所示
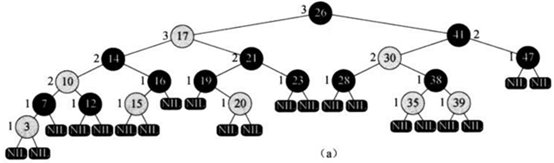
概念
左旋:
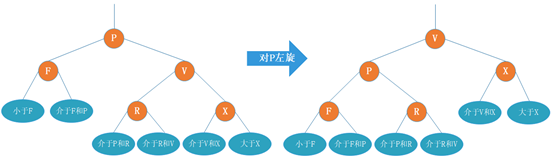
对P左旋即将P的右孩子V作为父节点,V的左孩子作为P的右孩子,左旋即P会变为左孩子。
// 左旋 LEFT_ROTATE(T, x) y = x.right // y 是 x 的右孩子 x.right = y.left // x 的右孩子更新为 y 的左孩子 if y.left != T.nil // y 的左孩子存在,更新 y 的左孩子的父辈关系 y.left.p = x y.p = x.p // 更新 y 的父辈关系 // 更新 y 的祖父辈关系 if x.p == T.nil // x 是根节点 T.root = y else if x == x.p.left x.p.left = y else x.p.right = y y.left = x // x 变更为 y 的左孩子 x.p = y // x 的父节点变更为 y
右旋:
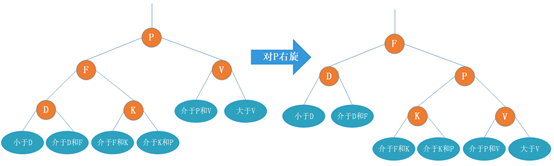
对P右旋即将P的左孩子V作为父节点(P的左孩子被使用了,那么需要补充新的左孩子),V的右孩子作为P的左孩子,右旋即P会变为右孩子。
// 右旋 RIGHT_ROTATE(T, x) y = x.left // y 是 x 的左孩子 x.left = y.right // x 的左孩子更新为 y 的右孩子 if y.right != T.nil // y 的右孩子存在,更新 y 的右孩子的父辈关系 y.right.p = x y.p = x.p // 更新 y 的父辈关系 // 更新 y 的祖父辈关系 if x.p == T.nil // x 是根节点 T.root = y else if x == x.p.left x.p.left = y else x.p.right = y y.right = x // x 变更为 y 的右孩子 x.p = y // x 的父节点变更为 y
旋转的目的
旋转主要为了修改黑高。
着色:
通过修改节点的颜色满足红黑树特性