Python实现自动微分(Automatic Differentiation)

2021-03-05

Python实现自动微分(Automatic Differentiation)

见：https://zhuanlan.zhihu.com/p/161635270?utm_source=wechat_session

什么是自动微分

自动微分(Automatic Differentiation)是什么？微分是函数在某一处的导数值，自动微分就是使用计算机程序自动求解函数在某一处的导数值。自动微分可用于计算神经网络反向传播的梯度大小，是机器学习训练中不可或缺的一步。

如何计算微分

微分计算离不开数学求导，如果你还对高等数学有些印象，大概记得如下求导公式：

常见求导公式

这些公式难免让人头大，好在自动微分就是帮助我们“自动”解决微分问题的。机器学习平台如TensorFlow、PyTorch都实现了自动微分，使用非常的方便，不过有必要理解其原理。要理解“自动微分”，需要先理解常见的求解微分的方式，可分为以下四种：

• 手动求解法(Manual Differentiation)
• 数值微分法(Numerical Differentiation)
• 符号微分法(Symbolic Differentiation)
• 自动微分法(Automatic Differentiation)

手动求解法

所谓手动求解法就是手动算出求导公式，然后将公式编写成计算机代码完成计算。比如对于函数  求微分，首先根据求导公式表找出其导数函数  ，然后将这个公式写成计算机程序，对于任意的输入  都能用这段程序求出其导数，也就是此时的微分。是不是很简单？

这样做虽然直观，但却有两个明显的缺点：

1. 每次都要根据手动算出求导公式然后编写代码，导致程序很难复用。
2. 更让人难受的是，复杂的函数普通人很难轻易写出求导公式

于是引出数值微分法。

数值微分法

数值微分法直接根据微分的极限定义形式：

只需要在  附近区一个很小的  (比如 0.00001)，分别计算  和  的值，然后做一个减法和除法就能得到此时的微分了，非常的直观。无论  是多么复杂的函数都可以带入上述公式求得微分。

该方法的缺陷是计算量太大，并且存在roundoff error和truncation error的问题。现实中仅仅常用它来验证其他自动微分程序的正确性，而不用于实际生产。

符号微分法

回顾“手动求解法”能联想到将常见求导公式写成固有函数，直接调用岂不是更方便？在此基础上基于链式求导法则对复杂公式求导，岂不是就解决了全部问题！

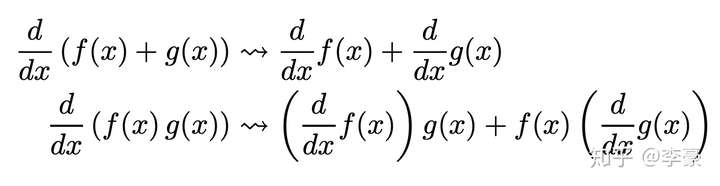链式求导法则

来看一下实际效果，下表展示了几个函数的符号微分公式：

符号微分公式

上图中第一列是原函数，第二列是符号微分法的计算公式，第三列是第二列的数学简化。即使是简化之后，微分计算公式也还要比原函数要复杂（更大的计算量）！所以这个方法也是理论上可行，实际上并不会采用。

自动微分

自动微分同时结合了“数值微分”和“符号微分”的长处，既对于已知函数直接采用数值微分法求取微分，并作为中间结果保存；对于组合函数采用符号微分法将公示展开，并将上一步数值微分的中间结果代入，二者结合降低了求解和计算的复杂度。

举个栗子，对于下列函数求解微分：

将上述公式转换为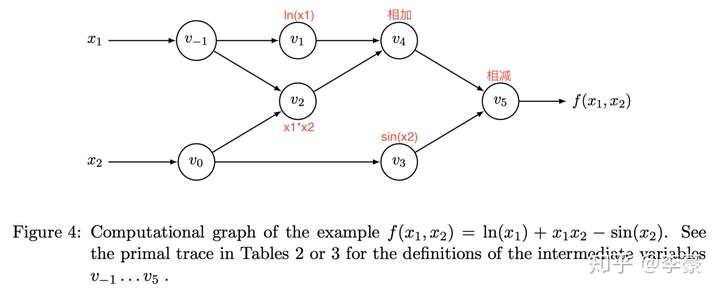计算图：

计算图

上图中每个圈圈表示操作产生中间结果，下标顺序表示他们的计算顺序。根据计算图我们一步步来计算函数的值，如下表所示，其中左侧表示数值计算过的过程，右侧表示梯度计算过程：

梯度求解过程(Forward mod)

表中计算了函数在  这一点的函数值和  的偏导数，整个计算过程结合者上图很容易理解。最终计算出  在  处的偏导数是5.5。如果要计算  的偏导数，还需要再重新计算一遍。相信你已经发现问题了：有多少个输入参数，这种偏导数计算流程就要执行多少遍。

有没有办法优化呢？答案是肯定的。就是将微分反向计算，把上面计算图的连线反向就得到了反向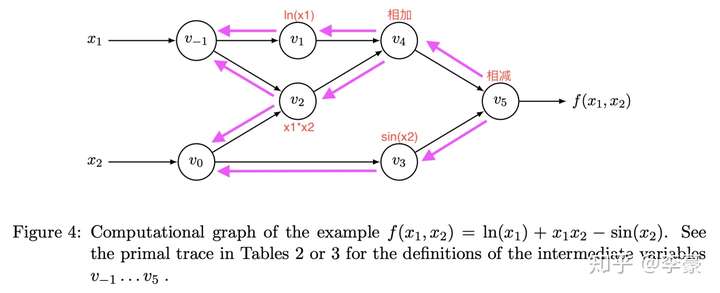计算图：

计算图

反向求微分流程如下：

自动微分(Reverse mode)

反向微分的好处是一次可以算出所有输入参数的偏导数，比如  在  处的偏导数分别是5.5和1.716。

Python代码实现

采用python代码实现自动微分程序。其中有三个关键类：

1. Op表示各种具体的操作，包括操作本身的计算和梯度计算。仅仅表示计算不保存操作的输入和状态，对应上面图中的一条边。
2. Node用于保存计算的状态，包括计算的输入参数、结果、梯度。每一次Op操作会产生新的Node，对应上面图中的一个圈圈。
3. Executor表示整个执行链路，用于正向对整个公式（在TensorFlow中叫做graph）求值以及反向自动微分。

为便于演示我们采用了eager执行的模式，既每个Node的值都是立即求得的。实际TensorFlow采用的是lazy模式，既首先构建公式然后再整体求值，这么做可以方便进行剪枝等优化操作，但不方便调试。

lazy模式的执行方式为，首先对计算图进行拓扑排序，然后按照拓扑排序的顺序从前往后依次求值。代码中Executor.run()方法演示了这个过程。其实着整个程序已经不仅仅是“自动微分”的演示了，而是tf图计算流程的演示，包括前向和后向（真实的算法模型中会使用更多种类的Op、模型本身也会更加复杂，但求解流程类似）

代码参考自CSE599G1的作业题：https://github.com/dlsys-course/assignment1 。为方便理解做了大量修改。

# -* encoding:utf-8 *-
import math

class Node(object):
  """
  表示具体的数值或者某个Op的数据结果。
  """
  global_id = -1
  
  def __init__(self, op, inputs):
    self.inputs = inputs # 产生该Node的输入
    self.op = op # 产生该Node的Op
    self.grad = 0.0 # 初始化梯度
    self.evaluate() # 立即求值
    # 调试信息
    self.id = Node.global_id
    Node.global_id += 1
    print("eager exec: %s" % self)
  
  def input2values(self):
    """ 将输入统一转换成数值，因为具体的计算只能发生在数值上 """
    new_inputs = []
    for i in self.inputs:
      if isinstance(i, Node):
        i = i.value
      new_inputs.append(i)
    return new_inputs

  def evaluate(self):
    self.value = self.op.compute(self.input2values())

  def __repr__(self):
    return self.__str__()

  def __str__(self):
    return "Node%d: %s %s = %s, grad: %.3f" % (
      self.id, self.input2values(), self.op.name(), self.value, self.grad)

class Op(object):
  """
  所有操作的基类。注意Op本身不包含状态，计算的状态保存在Node中，每次调用Op都会产生一个Node。
  """
  def name(self):
    pass
  
  def __call__(self):
    """ 产生一个新的Node，表示此次计算的结果 """
    pass

  def compute(self, inputs):
    """ Op的计算 """
    pass

  def gradient(self, output_grad):
    """ 计算梯度 """
    pass

class AddOp(Op): 
  """加法运算"""
  def name(self):
    return "add"

  def __call__(self, a, b):
    return Node(self, [a, b])
  
  def compute(self, inputs):
    return inputs[0] + inputs[1]
  
  def gradient(self, inputs, output_grad):
    return [output_grad, output_grad] # gradient of a and b

class SubOp(Op): 
  """减法运算"""
  def name(self):
    return "sub"

  def __call__(self, a, b):
    return Node(self, [a, b])
  
  def compute(self, inputs):
    return inputs[0] - inputs[1]
  
  def gradient(self, inputs, output_grad):
    return [output_grad, -output_grad]

class MulOp(Op): 
  """乘法运算"""
  def name(self):
    return "mul"
  
  def __call__(self, a, b):
    return Node(self, [a, b])
  
  def compute(self, inputs):
    return inputs[0] * inputs[1]

  def gradient(self, inputs, output_grad):
    return [inputs[1] * output_grad, inputs[0] * output_grad]

class LnOp(Op): 
  """自然对数运算"""
  def name(self):
    return "ln"

  def __call__(self, a):
    return Node(self, [a])

  def compute(self, inputs):
    return math.log(inputs[0])
  
  def gradient(self, inputs, output_grad):
    return [1.0/inputs[0] * output_grad]

class SinOp(Op): 
  """正弦运算"""
  def name(self):
    return "sin"

  def __call__(self, a):
    return Node(self, [a])

  def compute(self, inputs):
    return math.sin(inputs[0])
  
  def gradient(self, inputs, output_grad):
    return [math.cos(inputs[0]) * output_grad]

class IdentityOp(Op): 
  """输入输出一样"""
  def name(self):
    return "identity"

  def __call__(self, a):
    return Node(self, [a])

  def compute(self, inputs):
    return inputs[0]
  
  def gradient(self, inputs, output_grad):
    return [output_grad]

class Executor(object):
  """ 计算图的执行和自动微分 """

  def __init__(self, root):
    self.topo_list = self.__topological_sorting(root) # 拓扑排序的顺序就是正向求值的顺序
    self.root = root

  def run(self):
    """
    按照拓扑排序的顺序对计算图求值。注意：因为我们之前对node采用了eager模式，
    实际上每个node值之前已经计算好了，但为了演示lazy计算的效果，这里使用拓扑
    排序又计算了一遍。
    """
    node_evaluated = set() # 保证每个node只被求值一次
    print("
EVALUATE ORDER:")
    for n in self.topo_list:
      if n not in node_evaluated:
        n.evaluate()
        node_evaluated.add(n)
        print("evaluate: %s" % n)
    
    return self.root.value

  def __dfs(self, topo_list, node):
    if Node == None or not isinstance(node, Node):
      return
    for n in node.inputs:
      self.__dfs(topo_list, n)
    topo_list.append(node) # 同一个节点可以添加多次，他们的梯度会累加

  def __topological_sorting(self, root):
    """拓扑排序：采用DFS方式"""
    lst = []
    self.__dfs(lst, root)
    return lst

  def gradients(self):
    reverse_topo = list(reversed(self.topo_list)) # 按照拓扑排序的反向开始微分
    reverse_topo[0].grad = 1.0 # 输出节点梯度是1.0
    for n in reverse_topo:
      grad = n.op.gradient(n.input2values(), n.grad)
      # 将梯度累加到每一个输入变量的梯度上
      for i, g in zip(n.inputs, grad):
        if isinstance(i, Node):
          i.grad += g
    print("
AFTER AUTODIFF:")
    for n in reverse_topo:
      print(n)

# 开始验证程序
add, mul, ln, sin, sub, identity = AddOp(), MulOp(), LnOp(), SinOp(), SubOp(), IdentityOp()
x1, x2 = identity(2.0), identity(5.0)
y = sub(add(ln(x1), mul(x1, x2)), sin(x2)) # y = ln(x1) + x1*x2 - sin(x2)
ex = Executor(y)
print("y=%.3f" % ex.run())
ex.gradients() # 反向计算 自动微分
print("x1.grad=%.3f" % x1.grad)
print("x2.grad=%.3f" % x2.grad)

输出如下：

参考文献

https://blog.csdn.net/aws3217150/article/details/70214422

https://arxiv.org/pdf/1502.05767.pdf

http://dlsys.cs.washington.edu/schedule

https://github.com/dlsys-course/assignment1

编辑于 2020-08-01