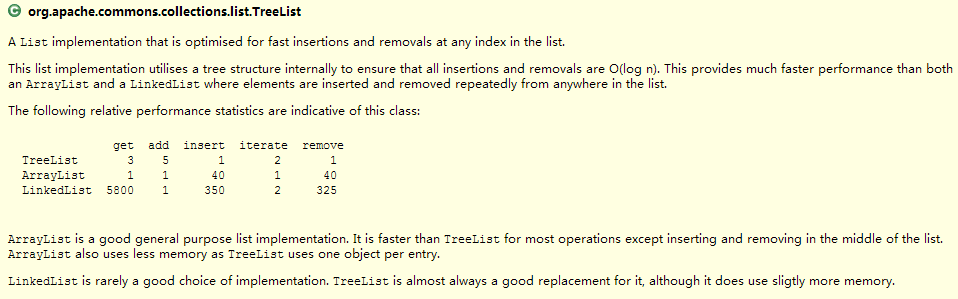
从这张图片说起:TreeList的实现结构:
首先是构建函数 TreeList(Collection coll),调用增加函数:
public void add(int index, Object obj) {
modCount++;
checkInterval(index, 0, size());
if (root == null) {
root = new AVLNode(index, obj, null, null);
} else {
root = root.insert(index, obj);
}
size++;
} //由此可以看出,Treelist采用的是平衡二叉树的实现的方式 ,并且以根节点作为成员变量,首先是AVL的数据结构:
static class AVLNode {
/** The left child node or the predecessor if {@link #leftIsPrevious}.*/
private AVLNode left;
/** Flag indicating that left reference is not a subtree but the predecessor. */
private boolean leftIsPrevious;
/** The right child node or the successor if {@link #rightIsNext}. */
private AVLNode right;
/** Flag indicating that right reference is not a subtree but the successor. */
private boolean rightIsNext;
/** How many levels of left/right are below this one. */
private int height;
/** The relative position, root holds absolute position. */
private int relativePosition;
/** The stored element. */
private Object value;
}
节点的新建:
private AVLNode(int relativePosition, Object obj, AVLNode rightFollower, AVLNode leftFollower) {
this.relativePosition = relativePosition;//相对的位置,index来进行标注
value = obj;
rightIsNext = true;
leftIsPrevious = true;
right = rightFollower;
left = leftFollower;
} 新建完成,根节点的建立,下一步就是继续的增加,采用的是插入的方式:
AVLNode insert(int index, Object obj) {
int indexRelativeToMe = index - relativePosition;
if (indexRelativeToMe <= 0) {
return insertOnLeft(indexRelativeToMe, obj);
} else {
return insertOnRight(indexRelativeToMe, obj);
}
}首先我们看 插入左节点:
private AVLNode insertOnLeft(int indexRelativeToMe, Object obj) {
AVLNode ret = this;
if (getLeftSubTree() == null) {
setLeft(new AVLNode(-1, obj, this, left), null);
} else {
setLeft(left.insert(indexRelativeToMe, obj), null);
}
if (relativePosition >= 0) {
relativePosition++;
}
ret = balance();
recalcHeight();
return ret;
}