玉米田【状压DP】【记搜】

题目大意：

农民 John 购买了一处肥沃的矩形牧场，分成M×N个格子。他想在那里的一些格子中种植美味的玉米。遗憾的是，有些格子区域的土地是贫瘠的，不能耕种。精明的 FJ 知道奶牛们进食时不喜欢和别的牛相邻，所以一旦在一个格子中种植玉米，那么他就不会在相邻的格子中种植，即没有两个被选中的格子拥有公共边。他还没有最终确定哪些格子要选择种植玉米。作为一个思想开明的人，农民 John 希望考虑所有可行的选择格子种植方案。由于太开明，他还考虑一个格子都不选择的种植方案！请帮助农民 John 确定种植方案总数。

---

思路：

DFS爆搜能拿90分，正解是状压DP。 
可以把可种植玉米的土地用1表示，贫瘠的土地用0表示，每一行串成的数字就是一个二进制数，状态压缩后，就成了一个较小的十进制数。 
设f[i][j]表示在第i行，状态压缩后的十进制数为j的情况下，总共种植的方案数。那么，若k&j=j，那么说明在上一行的种植情况为k时，这一行种植情况为jj是合法的（即没有两个玉米种植位置相连）。那么f[i][j]就与f[i−1][k]可以成立，f[i][j]+=f[i−1][k]。 
最终答案就是。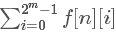

---

代码：

#include <cstdio>
#include <iostream>
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout);
using namespace std;

int n,m,a[21][21],g[21],f[21][5001],ms,num[41],sum;
bool state[5001];

int main()
{
    fre(cowfood);
    scanf("%d%d",&n,&m);
    num[1]=1;
    for (int i=2;i<=30;i++)
     num[i]=num[i-1]*2;  //为下面求2^i初始化
    for (int i=1;i<=n;i++)
     for (int j=1;j<=m;j++)
     {
        scanf("%d",&a[i][j]);
        g[i]=g[i]+num[j]*a[i][j];  //状态压缩
     }
    ms=num[m+1];  //2^m
    for (int i=0;i<ms;i++)
     state[i]=((!((i<<1)&i))&&(!((i>>1)&i)));  //初始化
    f[0][0]=1;
    for (int i=1;i<=n;i++)
     for (int j=0;j<ms;j++)
      if (state[j]&&((j&g[i])==j))  //为j的情况合法
       for (int k=0;k<ms;k++)
        if (!(j&k))  //k在上一行的情况合法
         f[i][j]+=f[i-1][k];
    for (int j=0;j<ms;j++)
     sum=(sum+f[n][j])%100000000;
    return printf("%d\n",sum)&0;
}