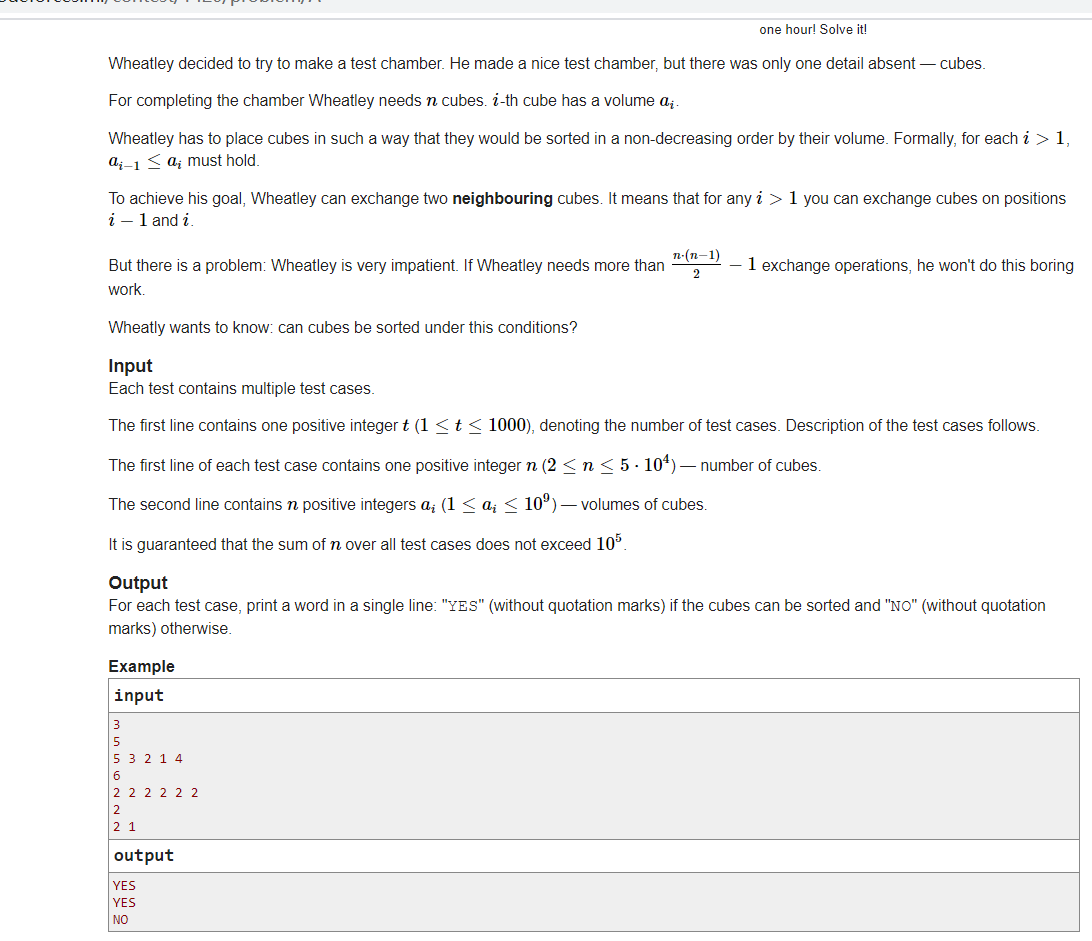
这道题我们需要把一个序列移动成递增序列,假设刚刚开始n个数是完全递减排列的
如 5 4 3 2 1,那么我们需要把1移动到第一个位置需要4步,2移动到第二个位置需要3步,以此类推,那么n个这样排列的数需要移动n-1+n-2+....+1,也就是(n-1)*n/2,与最大次数相差1,所以除了完全倒序排列的,其他情况都满足
附上代码
`#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
int a[N];
int main()
{
int t,n;
cin>>t;
while(t--)
{
cin>>n;
int sum=0;
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0;i<n-1;i++)
if(a[i]>a[i+1]) sum++; //如果每一个第i的数大于第i-1的数,那么sumn-1,即为完全递减的数列
if(sumn-1) cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
}
`