算法笔记--递归

1、n !

亦即n!=1×2×3×...×(n-1)n。阶乘亦可以递归方式定义：0!=1，n! = (n-1) ! × n

#include<cstdio>

int factorial(int n){
    if(n == 0)return 1;                 // 当到达递归边界F（0）时，返回F（0）==1
    else return factorial(n - 1) * n;   // 没有到达递归边界时，使用递归式递归下去
}

int main(){
    int n;
    scanf("%d", &n);
    printf("%d", factorial(n));
    return 0;
}

2、Fibonacci数列（斐波那契数列）

F(0) = 1, F(1) = 1, F(n) = F(n-1) + F(n-2) (n ≥ 2) 

数列的前几项为：1,1,2,3,5,8,13,21，...

递归边界为：F（0）= 1和 F（1）= 1，递归式：F(n) = F(n-1) + F(n-2) 

#include<cstdio>

int Fibonacci(int n){
    if(n == 0 || n == 1)return 1;                      // 递归边界
    else return Fibonacci(n - 1) + Fibonacci(n - 2);   // 递归式
}

int main(){
    int n;
    scanf("%d", &n);
    printf("%d", Fibonacci(n));
    return 0;
}

　　

3、全排列（Full Permutation）

#include<cstdio>

const int maxn = 11;
//P为当前排列，hashTable记录整数x是否已经在P中
int n, P[maxn], hashTable[maxn] = {false};
// 当前处理排列的第index号位
void generateP(int index){
    if(index == n + 1){          // 递归边界，已经处理完排列的1-n位
        for(int i=1; i <= n; i++){
            printf("%d", P[i]);  // 输出当前排列
        }
        printf("
");
        return;
    }
    for(int x=1; x <= n; x++){      // 枚举1-n，试图将x填入P[index]
        if(hashTable[x] == false){  // 如果x不在P[0]-p[index-1]中
            P[index] = x;           // 令P的第index位为x，即把x加入当前排列
            hashTable[x] = true;    // 记x已在P中
            generateP(index + 1);   // 处理排列的第index+1号位
            hashTable[x] = false;   // 已处理完P[index]为x的子问题，还原状态
        }
    }
}

int main(){
    n = 3;          // 欲输出1~3的全排列
    generateP(1);   // 从P[1]开始填
    return 0;
}

4、n皇后问题

由于每一行的不能有两个皇后，所以若有5*5的棋盘，则可视为1,2,3,4,5的全排列组合（相当于对棋盘按行存放），然后再检查是否符合条件。

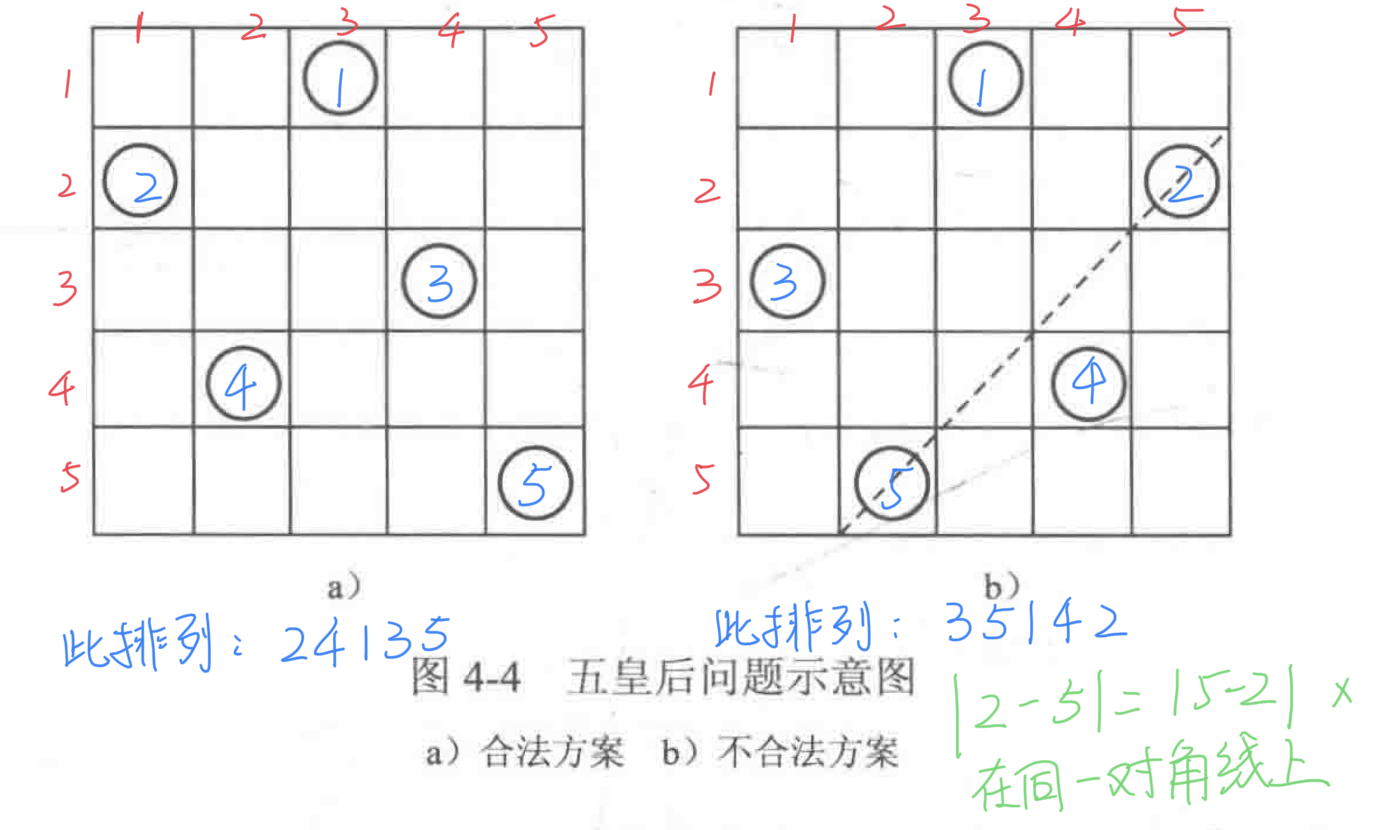 暴力法（先通过排列组合，再全部排查是否冲突）

#include<cstdio>
#include<cstdlib>
const int maxn = 11;
int count = 0;
bool hashTable[maxn] = {false};
int P[maxn];
int n;
void generateP(int index){
    if(index == n + 1){
        bool flag = true;
        for(int i=1; i <= n; i++){
            for(int j= i+1; j <= n; j++){
                if(abs(i - j) == abs(P[i] - P[j])){
                    flag = false;
                } // end if
            }     // end for j
        }         // end for i
        if(flag) count ++;
        return;
    }             // end if

    for(int x=1; x <=n; x++){
        if(hashTable[x] == false){
            P[index] = x;
            hashTable[x] =true;
            generateP(index + 1);
            hashTable[x] = false;
         }
    }
}

int main(){
    scanf("%d", &n);
    generateP(1);
    printf("%d", count);
    return 0;
}

回溯法（已放好n-1位，放置n位时检查是否冲突）

int P[maxn];
int n;
void generateP(int index){
    if(index == n + 1){
        count ++;
        return;
    }             // end if

    for(int x=1; x <=n; x++){
        if(hashTable[x] == false){
            bool flag = true;
            for(int pre=1; pre < index; pre++){
                if(abs(index - pre) == abs(x - P[pre])){
                    flag = false;
                    break;
                }
            }
            if(flag){
                P[index] = x;
                hashTable[x] = true;
                generateP(index + 1);
                hashTable[x] = false;
            }
         }
    }

}

int main(){
    scanf("%d", &n);
    generateP(1);
    printf("%d", count);
    return 0;
}

5、课后练习

算法笔记》4.3小节——算法初步->递归

问题 A: 吃糖果

题目描述
名名的妈妈从外地出差回来，带了一盒好吃又精美的巧克力给名名（盒内共有 N 块巧克力，20 > N >0）。
妈妈告诉名名每天可以吃一块或者两块巧克力。
假设名名每天都吃巧克力，问名名共有多少种不同的吃完巧克力的方案。
例如：
如果N=1，则名名第1天就吃掉它，共有1种方案；
如果N=2，则名名可以第1天吃1块，第2天吃1块，也可以第1天吃2块，共有2种方案；
如果N=3，则名名第1天可以吃1块，剩2块，也可以第1天吃2块剩1块，所以名名共有2+1=3种方案；
如果N=4，则名名可以第1天吃1块，剩3块，也可以第1天吃2块，剩2块，共有3+2=5种方案。
现在给定N，请你写程序求出名名吃巧克力的方案数目。

输入
输入只有1行，即整数N。

输出
可能有多组测试数据，对于每组数据，
输出只有1行，即名名吃巧克力的方案数。

样例输入
1
2
4

样例输出
1
2
5

递归边界：N = 1 or N =2;
递归式：eatCandy(N) = eatCandy(N - 1) + eatCandy(N - 2)

代码：

#include<cstdio>
#include<cstdlib>

int eatCandy(int N){
    if(N ==1)return 1;
    else if(N == 2)return 2;
    else return eatCandy(N - 1) + eatCandy(N - 2);
}

int main(){
    int n;
    while(scanf("%d", &n) != EOF){
        eatCandy(n);
        printf("%d
", n);
    }
    return 0;
}