问题叙述性说明:
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
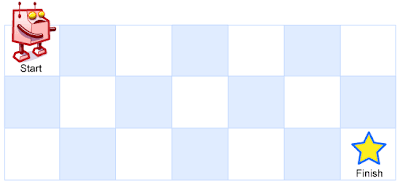
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
基本思想:
本题能够这么考虑。 设f[i][j]表示从左上到i行j列的格子处的全部路径数。考虑我们能够怎样到f[i][j]这个格子呢? 有两种方法:
- 从(i-1,j)向右走一步
- 从(i,j-1)向左走一步
所以我们能够列出恒等式 f[i][j] = f[i-1][j]+f[i][j-1];初始化(i,0)和(0,j)为1;如此便能够迭代的求出到最后右下时的方法数。
代码:
int uniquePaths(int m, int n) { //c++
if(m == 1 || n == 1)
return 1;
int array[m][n];
//init
for(int i = 0; i < n; i++)
array[0][i] = 1;
for(int i = 0; i < m; i++)
array[i][0] = 1;
for(int i = 1; i < m; i++)
for(int j = 1; j < n; j++){
array[i][j] = array[i-1][j]+array[i][j-1];
}
return array[m-1][n-1];
}版权声明:本文博客原创文章,博客,未经同意,不得转载。