至少原则平方多项式曲线拟合和实施

概念

最小二乘法多项式曲线拟合，依据给定的m个点,并不要求这条曲线精确地经过这些点，而是曲线y=f(x)的近似曲线y= φ(x)。

原理

[原理部分由个人依据互联网上的资料进行总结，希望对大家能实用]

     给定数据点pi(xi,yi)，当中i=1,2,…,m。求近似曲线y= φ(x)。而且使得近似曲线与y=f(x)的偏差最小。近似曲线在点pi处的偏差δi= φ(xi)-y，i=1,2,...,m。 

常见的曲线拟合方法:

     1.使偏差绝对值之和最小

     

     2.使偏差绝对值最大的最小

     

     3.使偏差平方和最小

     

     按偏差平方和最小的原则选取拟合曲线，而且採取二项式方程为拟合曲线的方法,称为最小二乘法。

推导过程：

     1. 设拟合多项式为：

          

     2. 各点到这条曲线的距离之和，即偏差平方和例如以下：

          

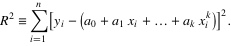
     3. 为了求得符合条件的a值，对等式右边求ai偏导数，因而我们得到了： 

          

          

                         .......

          

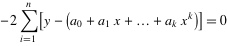
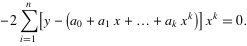
     4. 将等式左边进行一下化简，然后应该能够得到以下的等式：

          

          

                     .......

          

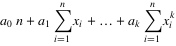
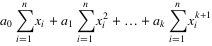
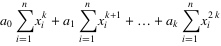
     5. 把这些等式表示成矩阵的形式，就能够得到以下的矩阵：

          

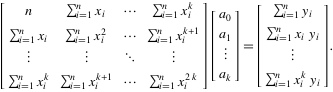
     6. 将这个范德蒙得矩阵化简后可得到:

          

     7. 也就是说X*A=Y，那么A = (X'*X)-1*X'*Y，便得到了系数矩阵A，同一时候，我们也就得到了拟合曲线。

实现

执行前提:

1. Python执行环境与编辑环境；
2. Matplotlib.pyplot图形库，可用于高速绘制2D图表，与matlab中的plot命令类似，并且使用方法也基本同样。

代码:

# coding=utf-8

'''
作者:Jairus Chan
程序:多项式曲线拟合算法
'''
import matplotlib.pyplot as plt
import math
import numpy
import random

fig = plt.figure()
ax = fig.add_subplot(111)

#阶数为9阶
order=9

#生成曲线上的各个点
x = numpy.arange(-1,1,0.02)
y = [((a*a-1)*(a*a-1)*(a*a-1)+0.5)*numpy.sin(a*2) for a in x]
#ax.plot(x,y,color='r',linestyle='-',marker='')
#,label="(a*a-1)*(a*a-1)*(a*a-1)+0.5"

#生成的曲线上的各个点偏移一下，并放入到xa,ya中去
i=0
xa=[]
ya=[]
for xx in x:
	yy=y[i]
	d=float(random.randint(60,140))/100
	#ax.plot([xx*d],[yy*d],color='m',linestyle='',marker='.')
	i+=1
	xa.append(xx*d)
	ya.append(yy*d)

'''for i in range(0,5):
	xx=float(random.randint(-100,100))/100
	yy=float(random.randint(-60,60))/100
	xa.append(xx)
	ya.append(yy)'''

ax.plot(xa,ya,color='m',linestyle='',marker='.')


#进行曲线拟合
matA=[]
for i in range(0,order+1):
	matA1=[]
	for j in range(0,order+1):
		tx=0.0
		for k in range(0,len(xa)):
			dx=1.0
			for l in range(0,j+i):
				dx=dx*xa[k]
			tx+=dx
		matA1.append(tx)
	matA.append(matA1)

#print(len(xa))
#print(matA[0][0])
matA=numpy.array(matA)

matB=[]
for i in range(0,order+1):
	ty=0.0
	for k in range(0,len(xa)):
		dy=1.0
		for l in range(0,i):
			dy=dy*xa[k]
		ty+=ya[k]*dy
	matB.append(ty)
 
matB=numpy.array(matB)

matAA=numpy.linalg.solve(matA,matB)

#画出拟合后的曲线
#print(matAA)
xxa= numpy.arange(-1,1.06,0.01)
yya=[]
for i in range(0,len(xxa)):
	yy=0.0
	for j in range(0,order+1):
		dy=1.0
		for k in range(0,j):
			dy*=xxa[i]
		dy*=matAA[j]
		yy+=dy
	yya.append(yy)
ax.plot(xxa,yya,color='g',linestyle='-',marker='')

ax.legend()
plt.show()

执行效果: 

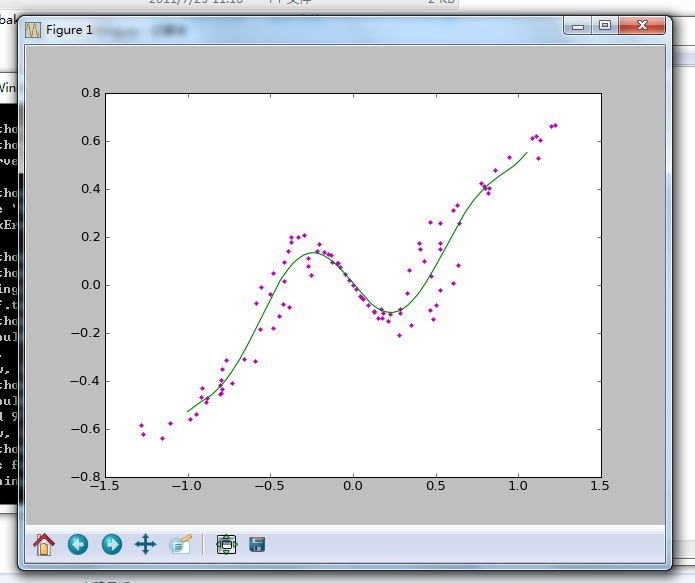
本博客中全部的博文都为笔者（Jairus Chan）原创。

如需转载，请标明出处：http://blog.csdn.net/JairusChan。

假设您对本文有不论什么的意见与建议，请联系笔者（JairusChan）。