决策树 Decision Tree

决策树是一个类似于流程图的树结构：其中，每个内部结点表示在一个属性上的测试，每个分支代表一个属性输出，而每个树叶结点代表类或类分布。树的最顶层是根结点。


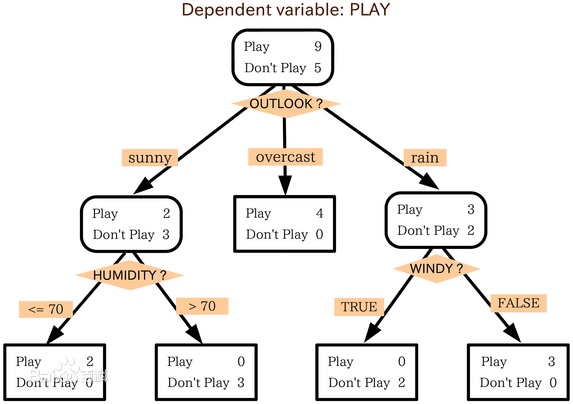
决策树的构建

想要构建一个决策树，那么咱们首先就需要有一定的已知信息来作为决策树的构建依据。

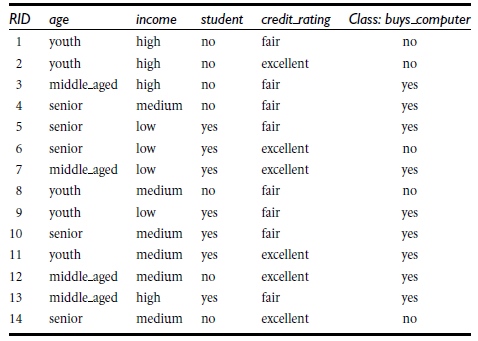
我们采用下图的数据来进行构建 决策树

一个完整的数据应该包括数据特征和对应的决策信息

下表中的数据，代表对购买电脑的客户信息的记录，分为age/imcome/student...等信息

在该数据源中，age 到 credit_rating 这4列称为特征，最后的class:buys_computer 代表最终的决策信息



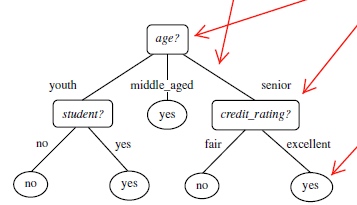
首先选择一个节点为开始（age），再根据该节点往下拓展，分为youth，middle_aged,seniors

根据这三类去上图的数据源检索，可以得出 当middle_aged时，clas_lable全部为yes，所以该分支就结束了。

重复上面的流程...知道最后的节点都是 决策结果信息



信息熵

流程和基本原理了解后，我们就要考虑一个问题：

信息，如何度量？

1948年，香农提出了 ”信息熵(entropy)“的概念
一条信息的信息量大小和它的不确定性有直接的关系，要搞清楚一件非常非常不确定的事情，或者是我们一无所知的事情，需要了解大量信息==>信息量的度量就等于不确定性的多少

      例子：猜世界杯冠军，假如一无所知，猜多少次？
      每个队夺冠的几率不是相等的

信息熵用 比特(bit) 来衡量信息的多少

信息熵公式为：


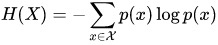
大写X代表信息集合
小写x代表集合中的某一
p(x)代表概率

假设 X={A，B，C}
A概率为0.2,
B概率为0.4,
C概率为0.6

那么计算结果为
-0.2 * log 0.2 +
-0.4 * log 0.4 +
-0.6 * log 0.6 的和

策树归纳算法 （ID3）

ID3算法是根据信息获取量(Information Gain)：
Gain(A) = Info(D) - Infor_A(D)
通过A来作为节点分类获取了多少信息




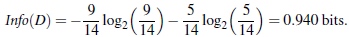
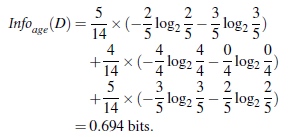
类似，Gain(income) = 0.029, Gain(student) = 0.151, Gain(credit_rating)=0.048

代码实现

数据源为第一个表格的数据

# 决策树
from sklearn.feature_extraction import DictVectorizer
import csv
from sklearn import tree
from sklearn import preprocessing
import pydotplus


# Read csv file
allElectronicsData = open('AllElectronics.csv','r')
csvReader = csv.reader(allElectronicsData)
# csvList = [ r for r in csvReader]
# print(csvList)
# 取头
headers = next(csvReader)

# print(headers)

featureList =[] #特征
labelList = []  #头


# 字典化所有特征
for row in csvReader:
    labelList.append(row[len(row) - 1])
    rowDic = {}
    for i in (range(1,len(row)-1)):
        rowDic[headers[i]] = row[i]
    # print(rowDic)
    featureList.append(rowDic)

print(featureList)
print(labelList)

# 矢量化 特征
vec = DictVectorizer()
dummyX = vec.fit_transform(featureList).toarray()

print("dummyX:")
print(str(dummyX))
print(vec.get_feature_names())

# 矢量化 class label
lb = preprocessing.LabelBinarizer()
dummyY = lb.fit_transform(labelList)
print("dummyY:")
print(dummyY)


# 构建决策树
clf = tree.DecisionTreeClassifier(criterion="entropy")
clf = clf.fit(dummyX,dummyY)
print("clf: ")
print(str(clf))

# 查看决策树
csvDot = tree.export_graphviz(clf,feature_names=vec.get_feature_names(),out_file=None)
graph = pydotplus.graph_from_dot_data(csvDot)
graph.write_pdf('1.pdf')
# Image(graph.create_png())


# 使用决策树计算
# 这里直接使用已经矢量化完事的数据来修改一下 进行预测，正常应该采用原始数据进行预处理后 进行预测
new_Data = dummyX[0, :]
print(dummyX[0, :])
# print(new_Data)
new_Data[0] = 0
new_Data[2] = 1
# print(new_Data)
# 预测该数据
predictedY = clf.predict([new_Data])
print(predictedY)