排序大的分类可以分为两种:内排序和外排序。在排序过程中,全部记录存放在内存,则称为内排序。如果排序过程中需要使用外存,则称为外排序。下面讲的排序都是属于内排序。
一、插入排序
(一)、直接插入排序
public class Sort { public static void main(String[] args) { int[] arr = {1, 3, 51, 65, 6, 34, 67, 343, 56}; int[] sortResult = insertionSort(arr); System.out.println(Arrays.toString(sortResult)); } /** * 用一个临时变量存储待插入的值,从后往前找,如果找到比这个值大的元素,则将其前面的元素依次后移, * 结束后再将带插入的值放到该插入的位置,减去了许多不必要的交换操作 * @param arr * @return */ public static int[] insertionSort(int[] arr) { for (int i = 1; i < arr.length; i++) { //待插入元素 int insertValue = arr[i]; int preIndex = i - 1; while (preIndex >= 0 && insertValue < arr[preIndex]) { arr[preIndex + 1] = arr[preIndex]; preIndex--; } arr[preIndex + 1] = insertValue; } return arr; } }
(二)、希尔排序(shell排序)
public class Sort { public static void main(String[] args) { int[] arr = {1, 3, 51, 65, 6, 34, 67, 343, 56}; int[] sortResult = shellSort(arr); System.out.println(Arrays.toString(sortResult)); } /** * 希尔排序 * 插入排序的升级版,设定步长为数组长度的一半,每次都除以二,直到步长为1 * @param arr * @return */ public static int[] shellSort(int[] arr) { int len = arr.length; for (int k = len / 2; k > 0; k /= 2) { for (int i = k; i < len; i++) { int temp = arr[i]; int j = i - k; while (j >= 0 && temp < arr[j]) { arr[j + k] = arr[j]; j -= k; } arr[j + k] = temp; } } return arr; } }
二、选择排序
(一)、简单选择排序(直接排序)
public class Sort { public static void main(String[] args) { int[] arr = {1, 3, 51, 65, 6, 34, 67, 343, 56}; int[] sortResult = selectionSort(arr); System.out.println(Arrays.toString(sortResult)); } /** * 遍历数组,每次遍历都找到最小的元素,记录其下标,内层循环结束后再根据下标将其与数组头部元素交换 * 与冒泡排序不同的是,冒泡排序每次循环可能交换多次,而选择排序最多交换一次 * @param arr 待排序数组 * @return */ public static int[] selectionSort(int[] arr) { int temp, minIndex; for (int i = 0; i < arr.length - 1; i++) { minIndex = i; for (int j = i + 1; j < arr.length; j++) { if (arr[j] < arr[minIndex]) { minIndex = j; } } temp = arr[minIndex]; arr[minIndex] = arr[i]; arr[i] = temp; } return arr; } }
(二)、堆排序
public class HeapSort { public static void main(String[] args) { int[] arr = {1, 3, 51, 65, 6, 34, 67, 343, 56}; int[] sortResult = heapSort(arr); System.out.println(Arrays.toString(sortResult)); } public static int[] heapSort(int[] arr) { //以最后一个非叶子结点构建大顶堆 for (int i = arr.length / 2 - 1; i >= 0; i--) { adjustHeap(arr, i, arr.length); } //此时顶部元素是最大的,交换顶部元素和末端元素 for (int i = arr.length - 1; i > 0; i--) { swap(arr, 0, i); //末端元素已经是最大的了,无需考虑排序 adjustHeap(arr, 0, i); } return arr; } /** * 形成大顶堆 * * @param arr 数组元素 * @param i 当前结点位置 * @param len 结点个数 */ public static void adjustHeap(int[] arr, int i, int len) { //保存当前结点 int temp = arr[i]; //遍历当前结点的左子结点 for (int k = 2 * i + 1; k < len; k = 2 * k + 1) { //如果右结点存在 且 右结点比左结点大,指向右结点 if (k + 1 < len && arr[k] < arr[k + 1]) { k++; } //判断当前结点和左(右)结点哪个大 if (temp < arr[k]) { //交换 swap(arr, k, i); //交换后,下次遍历以该子结点作为根节点的子树就会受到影响,因此需要重新指定下次的根节点 i = k; } else { //不用交换,直接终止循环 break; } } } public static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
三、交换排序
(一)、冒泡排序
/** * 遍历数组,依次比较相邻的元素并交换,每次都将最大元素(根据正序还是逆序决定)放到数组末尾 * @param arr 待排序数组 * @return */ public static int[] bubbleSort(int[] arr) { int temp; for (int i = 0; i < arr.length - 1; i++) { for (int j = 0; j < arr.length - i - 1; j++) { if (arr[j] > arr[j + 1]) { temp = arr[j + 1]; arr[j + 1] = arr[j]; arr[j] = temp; } } } return arr; }
冒泡排序优化一:
//冒泡排序:优化一 public static int[] bubbleSort1(int[] arr) { int temp; //记录数组是否有序 boolean isSorted; for (int i = 0; i < arr.length - 1; i++) { isSorted = true; for (int j = 0; j < arr.length - i - 1; j++) { if (arr[j] > arr[j + 1]) { temp = arr[j + 1]; arr[j + 1] = arr[j]; arr[j] = temp; //记录本轮排序是否交换了元素,如果交换则置为false isSorted = false; } } //没有交换证明已经是有序的了,直接终止循环 if (isSorted) { break; } } return arr; }
冒泡排序优化二:
//冒泡排序:优化二 public static int[] bubbleSort2(int[] arr) { int temp; boolean isSorted; //第一次循环边界 int sortBorder = arr.length - 1; //记录每轮排序最后一次进行交换的位置 int lastSwapIndex = 0; for (int i = 0; i < arr.length - 1; i++) { isSorted = true; for (int j = 0; j < sortBorder; j++) { if (arr[j] > arr[j + 1]) { temp = arr[j + 1]; arr[j + 1] = arr[j]; arr[j] = temp; isSorted = false; lastSwapIndex = j; } } sortBorder = lastSwapIndex; if (isSorted) { break; } } return arr; }
(二)、快速排序
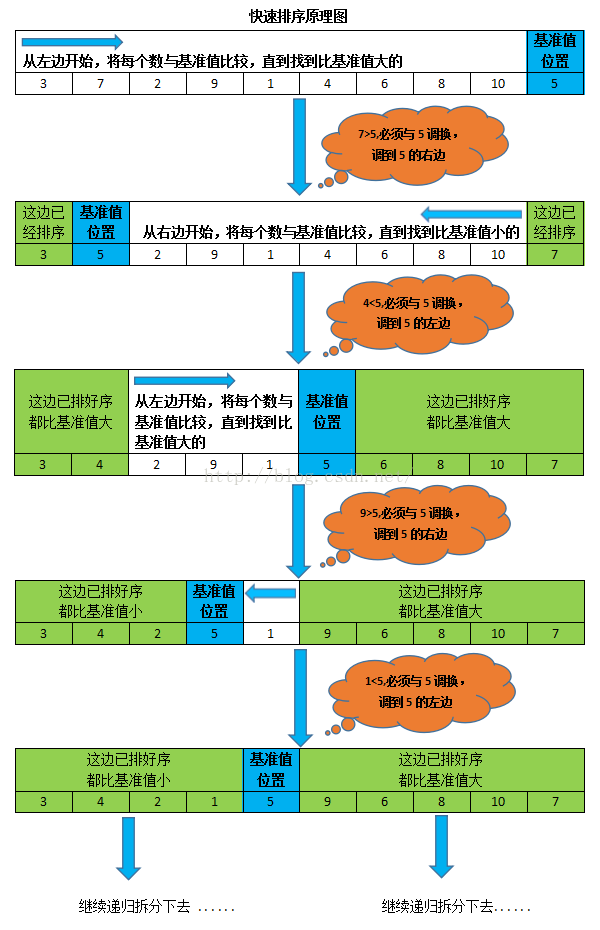
算法原理:先在数组中选择一个数字,通过一趟排序将要排序的数据分割成独立的两部分:比选择的数字小的数字都移到数组的左边,比选择的数字大的数字都移到数组的右边。然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序中基准的选取:
1. 第一个元素或最后一个元素,但是当数组中的元素原本为逆序时,升序排序就会变成一次只能确定基准元素的位置,无法发挥快排的优势
2. 随机选取
3. 三数取中法,也就是取左端、中间、右端三个数,然后进行排序,将中间数作为枢纽值。
举个栗子:
原数组:{3,7,2,9,1,4,6,8,10,5}
期望结果:{1,2,3,4,5,6,7,8,9,10}
快速排序示意图:
代码实现:
public class QuickSort { public static int divide(int[] a, int start, int end){ //每次都以最右边的元素作为基准值 int base = a[end]; //start一旦等于end,就说明左右两个指针合并到了同一位置,可以结束此轮循环。 while(start < end){ while(start < end && a[start] <= base) //从左边开始遍历,如果比基准值小,就继续向右走 start++; //上面的while循环结束时,就说明当前的a[start]的值比基准值大,应与基准值进行交换 if(start < end){ //交换 int temp = a[start]; a[start] = a[end]; a[end] = temp; //交换后,此时的那个被调换的值也同时调到了正确的位置(基准值右边),因此右边也要同时向前移动一位 end--; } while(start < end && a[end] >= base) //从右边开始遍历,如果比基准值大,就继续向左走 end--; //上面的while循环结束时,就说明当前的a[end]的值比基准值小,应与基准值进行交换 if(start < end){ //交换 int temp = a[start]; a[start] = a[end]; a[end] = temp; //交换后,此时的那个被调换的值也同时调到了正确的位置(基准值左边),因此左边也要同时向后移动一位 start++; } } //这里返回start或者end皆可,此时的start和end都为基准值所在的位置 return end; } /** * 排序 * @param a * @param start * @param end */ public static void sort(int[] a, int start, int end){ if(start > end){ //start >= end ? //如果只有一个元素,就不用再排下去了 return; } else{ //如果不止一个元素,继续划分两边递归排序下去 int partition = divide(a, start, end); sort(a, start, partition-1); sort(a, partition+1, end); } } public static void main(String[] args) { // TODO Auto-generated method stub int[] a = new int[]{2,7,4,5,10,1,9,3,8,6}; int[] b = new int[]{1,2,3,4,5,6,7,8,9,10}; int[] c = new int[]{10,9,8,7,6,5,4,3,2,1}; int[] d = new int[]{1,10,2,9,3,2,4,7,5,6}; int[] e = {3}; sort(b, 0, b.length-1); System.out.println("排序后的结果:"); for(int x : b){ System.out.print(x+" "); } } }
四、归并排序
public class Sort { public static void main(String[] args) { int[] arr = {1, 3, 51, 65, 6, 34, 67, 343, 56}; int[] sortResult = mergeSort(arr); System.out.println(Arrays.toString(sortResult)); } //归并排序 public static int[] mergeSort(int[] arr) { return mergeSort(arr, 0, arr.length - 1, new int[arr.length]); } /** * 归并排序通过递归将数组分解为只有两个元素,按照它们的大小放入到一个临时数组中,直到全部合并 * * @param arr 待排序数组 * @param left 左索引 * @param right 右索引 * @param temp 临时数组,存储每次合并后的元素 * @return */ public static int[] mergeSort(int[] arr, int left, int right, int[] temp) { if (left < right) { int mid = (left + right) >> 1; //向左分解 mergeSort(arr, left, mid, temp); //向右分解 mergeSort(arr, mid + 1, right, temp); //合并 merge(arr, left, mid, right, temp); } return arr; } //合并 public static int[] merge(int[] arr, int left, int mid, int right, int[] temp) { int i = left, j = mid + 1, k = 0; //按大小放入临时数组中 while (i <= mid && j <= right) { if (arr[i] < arr[j]) { temp[k] = arr[i]; k++; i++; } else { temp[k] = arr[j]; k++; j++; } } //将剩余元素放到temp剩余位置 while (i <= mid) { temp[k] = arr[i]; k++; i++; } while (j <= right) { temp[k] = arr[j]; k++; j++; } //将排好序的temp数组元素赋值给原数组 k = 0; int l = left; while (l <= right) { arr[l] = temp[k]; k++; l++; } return arr; } }
五、基数排序
public class RadixSort { public static void main(String[] args) { int[] arr = {1, 3, 51, 65, 6, 34, 67, 343, 56}; int[] sortResult = radixSort(arr); System.out.println(Arrays.toString(sortResult)); } /** * 基数排序: * 根据每个数的个位、十位、百位...的值(0~9)放入桶中(规则和计数排序相同),因此需要10个桶 * * @param arr * @return */ public static int[] radixSort(int[] arr) { //创建并初始化10个桶 ArrayList<LinkedList<Integer>> bucketList = new ArrayList<>(10); for (int i = 0; i < 10; i++) { bucketList.add(new LinkedList<>()); } //找出数据中最大值 int max = arr[0]; for (int i = 1; i < arr.length; i++) { if (max < arr[i]) { max = arr[i]; } } //获取最大值的位数 int maxRadix = (max + "").length(); //从个位开始 for (int i = 0; i < maxRadix; i++) { //将待排序元素放入桶中 for (int j = 0; j < arr.length; j++) { //获取数字对应位上的值 int radix = arr[j] / (int) Math.pow(10, i) % 10; //放入对应的桶中 bucketList.get(radix).add(arr[j]); } //将桶中元素放回原数组 int k = 0; for (int j = 0; j < 10; j++) { for (Integer number : bucketList.get(j)) { arr[k++] = number; } bucketList.get(j).clear(); } } return arr; } }
另:排序算法的稳定性
1. 稳定性的定义
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,ri=rj,且ri在rj之前,而在排序后的序列中,ri仍在rj之前,则称这种排序算法是稳定的;否则称为不稳定的。
举个栗子:以{6,2,4,6,1}为例
| a[0] | a[1] | a[2] | a[3] | a[4] |
| 6 | 2 | 4 | 6 | 1 |
有两个6,a[0]和a[3]。排序结果就有两种可能:
| 1 | 2 | 4 | 6 | 6 |
| 原a[4] | 原a[1] | 原a[2] | 原a[0] | 原a[3] |
| 原a[4] | 原a[1] | 原a[2] | 原a[3] | 原a[0] |
如果排序结束后,a[0]可以保证一定在a[3]前头,也就是他们原有的顺序不变,那这种排序算法就是稳定的。反之,如果不能保证原有顺序,这种算法就是不稳定的。
2. 常见算法的稳定性
堆排序、快速排序、希尔排序、直接选择排序不是稳定的排序算法,而基数排序、冒泡排序、直接插入排序、折半插入排序、归并排序是稳定的排序算法。
3. 稳定性的意义
1、如果只是简单的进行数字的排序,那么稳定性将毫无意义。
2、如果排序的内容仅仅是一个复杂对象的某一个数字属性,那么稳定性依旧将毫无意义(所谓的交换操作的开销已经算在算法的开销内了,如果嫌弃这种开销,不如换算法好了?)
3、如果要排序的内容是一个复杂对象的多个数字属性,但是其原本的初始顺序毫无意义,那么稳定性依旧将毫无意义。
4、除非要排序的内容是一个复杂对象的多个数字属性,且其原本的初始顺序存在意义,那么我们需要在二次排序的基础上保持原有排序的意义,才需要使用到稳定性的算法。例如要排序的内容是一组原本按照价格高低排序的对象,如今需要按照销量高低排序,使用稳定性算法,可以使得想同销量的对象依旧保持着价格高低的排序展现,只有销量不同的才会重新排序。(当然,如果需求不需要保持初始的排序意义,那么使用稳定性算法依旧将毫无意义)。
参考:
https://www.cnblogs.com/songjilong/p/12234856.html
https://blog.csdn.net/sunxianghuang/article/details/51872360
https://blog.csdn.net/it_zjyang/article/details/53406764
https://www.cnblogs.com/hydor/p/3530593.html
https://blog.csdn.net/chenliguan/article/details/53037482
