http://poj.org/problem?id=1273
最大流算法:
一张图有一个源点一个汇点,中间有很多要经过的点,点与点之间有最大流量的限制,问从源点到汇点的最大每秒流量是多少
加入了残余网络和增广路这两个概念
残余网络:是对于一次处理之后得到得剩下的图
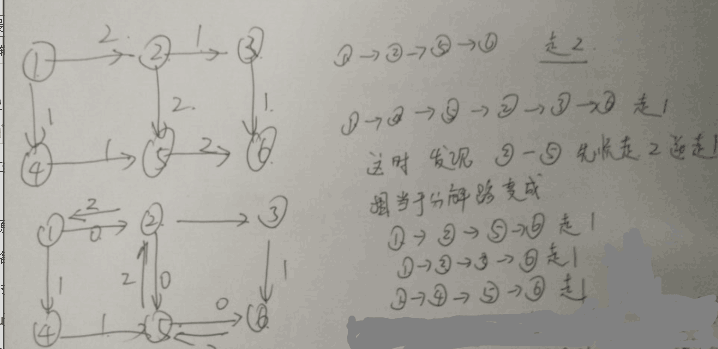
增广路:对于u到i的的流量我少了x容量那么i到u我反向多个x容量,保证能够反悔不走这条路
EK算法复杂度O(VM) V:最大容量 M:边数
具体证明:http://www.cnblogs.com/luweiseu/archive/2012/07/14/2591573.html java代码看的头晕~~

代码实现:
/************************************************
* Author :Powatr
* Created Time :2015-8-24 19:40:52
* File Name :POJ1273_EK.cpp
************************************************/
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cstring>
#include <cmath>
#include <string>
#include <vector>
#include <queue>
#include <deque>
#include <stack>
#include <list>
#include <map>
#include <set>
#include <bitset>
#include <cstdlib>
#include <ctime>
using namespace std;
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
typedef long long ll;
const int MAXN = 2e2 + 10;
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
int pre[MAXN];
int n, m, ans;
int mp[MAXN][MAXN];
queue<int> q;
void EK()
{
while(1){
memset(pre, 0, sizeof(pre));
while(!q.empty()) q.pop();
q.push(1);
while(!q.empty()){
int now = q.front(); q.pop();
if(now == m) break;
for(int i = 1; i <= m; i++){
if(mp[now][i] > 0 && !pre[i]){
pre[i] = now;
q.push(i);
}
}
}
if(pre[m] == 0) break;
int min1 = INF;
for(int i = m; i != 1; i = pre[i])
min1 = min(min1, mp[pre[i]][i]);
for(int i = m; i != 1 ; i = pre[i]){
mp[pre[i]][i] -= min1;
mp[i][pre[i]] += min1;
}
ans += min1;
}
}
int main(){
while(~scanf("%d%d", &n, &m)){
ans = 0;
memset(mp, 0, sizeof(mp));
int u, v, val;
for(int i = 1; i <= n; i++){
scanf("%d%d%d", &u, &v, &val);
mp[u][v] += val;
}
EK();
printf("%d
", ans);
}
return 0;
}