数论专题
前言:总结一下之前学的数论内容
1.素数与唯一分解定理
(0) 素数
显然大于1的正整数\(a\)可以1和 \(a\) 整除,如果除此之外 \(a\) 没有其他的约数,则称 \(a\)是素数,又称质数。任何一个大于1的整数如果不是素数,也就是有其他约数,就称为是合数。
0既不是合数也不是素数。
(1) 素数计数函数
对于小于或等于 \(x\) 的素数的个数,用 \(π(x)\) 表示。随着 \(x\) 的增大,有这样的近似结果:
(2)唯一分解定理
唯一分解定理又称为算数基本定理,基本内容是:
每个大于1的自然数,要么本身就是质数,要么可以写为2个或以上的质数的积,而且这些质因子按大小排列之后,写法仅有一种方式。
另一种方法表示就是:
对于任何一个大于1的正整数,都存在一个标准的分解式
\(a=p_1^{r_1}p_2^{r_2}...p_n^{r_n},b=p_1^{s_1}p_2^{s_2}...p_n^{s_n}\)
此定理表明:任何一个大于 1 的正整数都可以表示为素数的积。
(3) 质因数分解
void func(int x,vector<int>& r){
r.clear();
for(int i=2;i<=sqrt(x);i++){
if(x%i==0){
while(x%i==0){
x/=i;
r.push_back(i);
}
}
}
if(x!=1) r.push_back(x);
}
//O(sqrt(x))
void func(int x,vector<int>& r){
r.clear();
for(int i=2;i<=sqrt(x);i++){
if(x%i==0){
while(x%i==0){
x/=i;
r.push_back(i);
}
if(isprime(x)) break;
}
}
if(x!=1) r.push_back(x);
}
//一个简单优化
(4) 素数判断:试除法
暴力做法自然可以枚举从小到大的每个数看是否能整除
但很容易发现这样一个事实:如果 \(x\) 是 \(a\) 的约数,那么 \(\frac{a}{x}\) 也是 \(a\) 的约数。
这个结论告诉我们,对于每一对 \((x,\frac{a}{x})\) ,只需要检验其中的一个就好了。为了方便起见,我们只考察每一对里面小的那个数。不难发现,所有这些较小数就是 $ [1,\sqrt{a}]$ 这个区间里的数。
由于1肯定是约数,所以不检验它。
bool isPrime(a) {
if (a < 2) return 0;
for (int i = 2; i * i <= a; ++i)
if (a % i == 0) return 0;
return 1;
}
(5) 伯特兰—切比雪夫定理
伯特兰—切比雪夫定理说明:若整数\(n > 3\),则至少存在一个质数\(p\),符合\(n < p < 2n − 2\)。
另一个稍弱说法是:对于所有大于\(1\)的整数\(n\),至少存在一个质数\(p\),符合\(n < p < 2n\)。
其中两个加强结果(定理):
定理 1: 对任意自然数\(n > 6\), 至少存在一个\(4k + 1\)型和一个\(4k + 3\)型素数 \(p\) 使得\(n < p < 2n\)。
定理 2: 对任意自然数\(k\), 存在自然数\(N\), 对任意自然数 \(n > N\)至少存在\(k\) 个素数\(p\)使得 \(n < p < 2n\)。
相关例题:洛谷P5535 小道消息
2.素数筛法
(1) Eratosthenes 筛法 (埃拉托斯特尼筛法)
时间复杂度是\(O(nloglogn)\) 。
int Eratosthenes(int n)
{
int p = 0;
for (int i = 0; i <= n; ++i) is_prime[i] = 1;
is_prime[0] = is_prime[1] = 0;
for (int i = 2; i <= n; ++i) {
if (is_prime[i]) {
prime[p++] = i; // prime[p]是i,后置自增运算代表当前素数数量
if ((long long)i * i <= n)
for (int j = i * i; j <= n; j += i)
// 因为从 2 到 i - 1 的倍数我们之前筛过了,这里直接从 i
// 的倍数开始,提高了运行速度
is_prime[j] = 0; // 是i的倍数的均不是素数
}
}
return p;
}
(2) Euler 筛法 (欧拉筛法、线性筛法)
时间复杂度\(O(n)\)。
代码中,外层枚举 \(i = 1 \to n\)。对于一个 \(i\) ,经过前面的腥风血雨,如果它还没有被筛掉,就加到质数数组 \(Prime[]\) 中。下一步,是用 \(i\) 来筛掉一波数。
内层从小到大枚举\(Prime[j]\)。 \(i×Prime[j]\) 是尝试筛掉的某个合数,其中,我们期望 \(Prime[j]\) 是这个合数的最小质因数 (这是线性复杂度的条件,下面叫做“筛条件”)。它是怎么得到保证的?
\(j\) 的循环中,有一句就做到了这一点:
if(i % Prime[j] == 0)
break;
-
下面用 \(s(smaller)\) 表示小于 \(j\)的数,\(L(larger)\) 表示大于 \(j\) 的数。
-
① \(i\) 的最小质因数肯定是 \(Prime[j]\)。
(如果 \(i\) 的最小质因数是 \(Prime[s]\) ,那么 \(Prime[s]\) 更早被枚举到(因为我们从小到大枚举质数),当时就要break)
既然 \(i\) 的最小质因数是 \(Prime[j]\),那么 \(i×Prime[j]\) 的最小质因数也是 \(Prime[j]\)。所以,\(j\) 本身是符合“筛条件”的。
- ② \(i×Prime[s]\) 的最小质因数确实是 \(Prime[s]\)。
(如果是它的最小质因数是更小的质数 \(Prime[t]\),那么当然 \(Prime[t]\) 更早被枚举到,当时就要break)
这说明 \(j\) 之前(用 \(i×Prime[s]\) 的方式去筛合数,使用的是最小质因数)都符合“筛条件”。
- ③ \(i×Prime[L]\) 的最小质因数一定是 \(Prime[j]\)。
(因为 \(i\) 的最小质因数是 \(Prime[j]\),所以 \(i×Prime[L]\) 也含有 \(Prime[j]\) 这个因数(这是 \(i\) 的功劳),所以其最小质因数也是 \(Prime[j]\)(新的质因数 \(Prime[L]\) 太大了))
这说明,如果 \(j\) 继续递增(将以 \(i×Prime[L]\) 的方式去筛合数,没有使用最小质因数),是不符合“筛条件”的。
#include <bits/stdc++.h>
using namespace std;
bool isprime[100000010];
int prime[6000010];
int cnt = 0;
void getprime(int n)
{
memset(isprime,1,sizeof(isprime));
isprime[1] = 0;//1不是素数
for(int i=2;i<=n;i++)
{
if(isprime[i]) prime[++cnt] = i;
for(int j=1;j<=cnt;j++)
{
if(i*prime[j]>n) break;
isprime[i*prime[j]] = 0;
if(i % prime [j] == 0) break;
}
}
}
int main()
{
int n,q;
scanf("%d%d",&n,&q);
getprime(n);
while(q--)
{
int k;
scanf("%d",&k);
printf("%d\n",prime[k]);
}
return 0;
}
3.最大公约数(gcd)
求最大公因数
法1:更相减损术
//下面这个gcd函数在正int型内完全通用,返回a,b的最大公因数。
//但是当a,b之间差距较大时(如100000倍)会导致错误(栈过深)
int gcd(int a,int b){
if(a==b)return a;
else if(a>b)a-=b;
else b-=a;
return gcd(a,b);
}
int main(){
int a,b;
cin>>a>>b;
cout<<gcd(a,b)<<endl;
return 0;
}
计算需要相减多少次
int gg(int x,int y){
if(y==0) return a;
cnt+=a/b;
return gg(b,a%b);
}//计算需要相减多少次
法2:辗转相除法(欧几里得算法)
int gcd(int a,int b)
{
if(b==0) return a;
else return gcd(b,a%b);
}
直接在法1改进,效率倍增
法3:一个接近定理的东西:质因数分解
由于唯一分解定理,对\(a,b\)进行素因子分解:
\(a=p_1^{r_1}p_2^{r_2}...p_n^{r_n},b=p_1^{s_1}p_2^{s_2}...p_n^{s_n}\)
注意:\(r_1\),\(s_2\)等代表质因子需要乘的次数
则有
关于求最小公倍数(lcm)
不难验证\(a*b=\gcd (a,b) * lcm (a,b)\)
那么\(lcm (a,b) = a*b/gcd(a,b)\)
由于 \(a*b\) 有可能溢出
正确的写法一般是先除后乘法,即为
\(lcm (a,b) = a/gcd(a,b)*b\)
4.拓展欧几里得算法(exgcd)
用于求解形如\(ax+by=gcd(a,b)\)的不定方程特解。
当\(b=0\)时,可以看出\(gcd(a,b)=a\),而
此时
(实际上此时y大小不影响代码实现)
当\(b≠0\)时,递归求解\(exgcd(b,a\ mod\ b,x,y)\),设
可以求得\(a'x'+b'y'=gcd(a,b)\)的一组特解,即\(x'\),\(y'\)。
所以得到了递归结束后\(x\),\(y\)的表达式
证明如下:
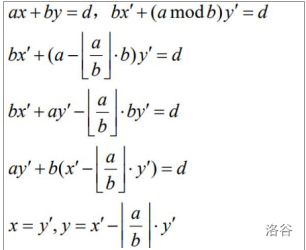
代码:
void exgcd(int a,int b,int &x,int &y)
{
if(!b)
{
x=1;
y=0;
return;
}
exgcd(b,a%b,x,y);
int p;
p=x;
x=y;
y=p-(a/b)*y;//x=y',y=x'-(a/b)*y'
return;
}
还有一种更短的
void exgcd(int a,int b,int &x,int &y)
{
if(!b)
{
x=1;y=0;
return;
}
exgcd(b,a%b,y,x)//x=y',y=x'
y-=(a/b)*x;//y=x'-(a/b)*y'
return;
}
根据递归,我们可以知道这个x,y特解满足
|x|+|y|最小
但是我们不满足求这一组解
如果设
\(d = gcd(a,b)\)
那么:

所以x,y的解可以写成\((x_0+kb',y_0-ka')\)
在此时,我们可以求出x,y最小非负整数解
分别是
xin=(x%b+b)%b;//最小非负整数解
yin=(y%a+a)%a;//最小非负整数解
xin=x>0&&x%b!=0?x%b:x%b+b;//最小正整数解
yin=y>0&&y%a!=0?y%a:y%a+a;//最小正整数解
//最大整数解可以通过代入求出
当然,我们看到上面的求证过程中一直没有出现用到
“\(ax+by\)右面是什么”
那么我们可以推广:
设a,b,c为任意整数,若方程\(ax+by=c\)其中一个解是\((x_0,y_0)\)
则它的任意整数解可以写成 \((x_0+kb',y_0-ka')\)
由此我们知道了任意整数解的求法,那\(ax+by=c\)的特解怎么求呢?

这里给出了一般性的做法,但为了编写代码方便
我们一般这么做
设
则
此时\(gcd(a',b')=1\),可以利用exgcd求出\(a'x'+b'y'=1\)的一组特解,继而得出
我们便求得了\(ax+by=c\)的一组特解。
这里给出p5656的代码
//exgcd
#include <bits/stdc++.h>
#define int long long
using namespace std;
int gcd(int a,int b)
{
if(b==0) return a;
else return gcd(b,a%b);
}
void exgcd(int a,int b,int &x,int &y)
{
if(!b)
{
x=1;
y=0;
return;
}
exgcd(b,a%b,x,y);
int p;
p=x;
x=y;
y=p-(a/b)*y;//x=y',y=x'-(a/b)*y'
return;
}
signed main()
{
int t;
scanf("%lld",&t);
while(t--)
{
int a,b,c,x=0,y=0,xin,xax,yin,yax,npa=0,g;//分别是x,y最小,最大正整数解 ,和正整数解的数量
scanf("%lld%lld%lld",&a,&b,&c);
g=gcd(a,b);
if(c%g!=0) printf("-1\n");//裴蜀定理
else
{
a/=g;
b/=g;
c/=g;//eg:求6x+15y=15:a:6/3=2,b:15/3=5,c:15/3=5
//求2x'+5y'=1的一组解,x'=-2,y'=1
//则原解为x'*c,x=-10,y=5;
exgcd(a,b,x,y);//a'x+b'y=1
x*=c;
y*=c;
//xin=(x%b+b)%b;最小非负整数解
xin=x>0&&x%b!=0?x%b:x%b+b;
yax=(c-a*xin)/b;
//yin=(y%a+a)%a;最小非负整数解
yin=y>0&&y%a!=0?y%a:y%a+a;
xax=(c-b*yin)/a;
if(xax>0)//yax>0也行
npa=(xax-xin)/b+1;//正整数解数量
//npa=(yax-yin)/a+1;
if(npa==0)
{
printf("%lld %lld\n",xin,yin);
}
else printf("%lld %lld %lld %lld %lld\n",npa,xin,yin,xax,yax);
}
}
return 0;
}
5.线性同余方程
对于形如 \(ax≡c(mod\ b)\) 的线性同余方程,
根据模运算的定义,在方程左侧添加一个\(by\)不会对结果造成影响,其实质就等价于\(ax+by=c\)的不定方程,利用exgcd求解便可。
注意:\(a≡c(mod\ b)\)有解的充要条件是:\(a-c\)是\(b\)的整数倍
又因为它与\(ax+by = c\) 等价,那么它有整数解的充要条件也是:
\(gcd(a,b)|c\)
例题:
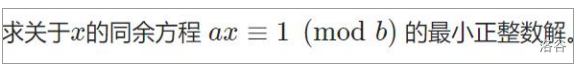
转换成\(ax\ mod\ b=1\)
转换成移项可得\(ax+by=1\)(保证y是负数)
之后用exgcd求解
代码:
//转化为求解ax+by=1
#include <bits/stdc++.h>
using namespace std;
void exgcd(int a,int b,int &x,int &y)
{
if(!b)
{
x=1;y=0;
return;
}
exgcd(b,a%b,x,y);
int temp=x;
x=y;
y=temp-(a/b)*y;
}
int main()
{
int a,b,x,y;
scanf("%d%d",&a,&b);
exgcd(a,b,x,y);
x=x>0&&x%b!=0?x%b:x%b+b;
printf("%d",x);
return 0;
}
拓展性质:
$ax \equiv 1(mod\ b $称为同余方程的“逆”:a与b互质,且有唯一解
(注意:线性方程的唯一解是一组解)
它也是求解逆元的方法。。
6.乘法逆元
乘法逆元,一般用于求 \(\frac{a}{b} \pmod p\) 的值(\(p\)通常为质数),是解决模意义下分数数值的必要手段。
(1) exgcd
模数可以 不为质数
这个方法十分容易理解,而且对于单个查找效率似乎也还不错(尤其对于$ \bmod {p} $比较大的时候)。
这个就是利用拓欧求解 线性同余方程$ ax \equiv c \pmod {b}\(的\)c=1\(的情况。我们就可以转化为解\) ax + b*y = 1$这个方程。
求解这个方程的解。
而且这个做法还有个好处在于,当$ a \bot p$(互质),但 \(p\) 不是质数的时候也可以使用。
代码比较简单:
void Exgcd(ll a, ll b, ll &x, ll &y) {
if (!b) x = 1, y = 0;
else Exgcd(b, a % b, y, x), y -= a / b * x;
}
int main() {
ll x, y;
Exgcd (a, p, x, y);
x = (x % p + p) % p;
printf ("%d\n", x); //x是a在mod p下的逆元
}
(2) 费马小定理
只适用于模数为质数的情况
若\(p\)为素数,\(a\)为正整数,且\(a\)、\(p\)互质。 则有\(a^{p-1} \equiv 1 (\bmod {p})\)。
另一个形式:
对于任意整数 $a $ ,有\(a^p \equiv \ a (mod \ p)\)
观察第一个公式:
这个我们就可以发现它这个式子右边刚好为 1 。
所以我们就可以放入原式,就可以得到:
\(a*x\equiv 1 \pmod p\)
\(a*x\equiv a^{p-1} \pmod p\)
$x \equiv a^{p-2} \pmod p $
所以我们可以用快速幂来算出 \(a^{p-2} \pmod p\)的值,这个数就是它的逆元了
ll fpm(ll x, ll power, ll mod) {
x %= mod;
ll ans = 1;
for (; power; power >>= 1, (x *= x) %= mod)
if(power & 1) (ans *= x) %= mod;
return ans;
}
(3) 线性算法
只适用于模数为质数的情况
用于求一连串数字对于一个\(\bmod p\)的逆元。保证\(n<p\)
只能用这种方法,别的算法都比这些要求一串要慢。
首先我们有一个,\(1^{-1}\equiv 1 \pmod p\)
然后设$ p=k*i+r,(1<r<i<p)$也就是 $ k$ 是 $ p / i$ 的商, $r $ 是余数 。
再将这个式子放到\(\pmod p\)意义下就会得到:
\(k*i+r \equiv 0 \pmod p*\)
然后乘上\(i^{-1},r^{-1}\)就可以得到:
\(k*r^{-1}+i^{-1}\equiv 0 \pmod p\)
\(i^{-1}\equiv -k*r^{-1} \pmod p\)
\(i^{-1}\equiv -\lfloor \frac{p}{i} \rfloor*(p \bmod i)^{-1} \pmod p\)
于是,我们就可以从前面推出当前的逆元了。
注意:$ i ^{-1} * i ^{1} \equiv 1 $
#include <bits/stdc++.h>
#define ll long long
#define N 3000010
using namespace std;
ll inv[N];
int main()
{
int n,p;
scanf("%d%d",&n,&p);
inv[1]=1;
printf("1\n");
for(int i=2;i<=n;i++)
{
inv[i]=(ll)(p-p/i)*inv[p%i]%p;
printf("%lld\n",inv[i]);
}
return 0;
}
(4) 阶乘逆元法
只适用于模数为质数的情况
设$ f(i)=inv(i!)$, $ g(i)=i!\ $
则:$ f(i-1) = f(i) \times i $
- 证明:
$f(i-1)=\frac{1}{\ (i-1)\ !}=\frac{1}{i\ !}\times i =f(i)\times i $
假设要求 \([1,n]\) 中所有数的逆元
先求得 \([1,n]\) 中所有数的阶乘
再用费马小定理 求得\(f(n)\)的值
之后递推出 \(f(1 \sim n)\) 的值
但是 \(inv(1! \sim n! )\) 并不是我们想要的答案
需要继续转化。
可知 : $inv(i) = inv(i!) \times(i-1)\ ! $
-
证明 :
\(inv(i)=\frac{1}{i}=\frac{1}{i\ !}\times (i-1)\ ! = inv(i!)\times (i-1)!\)
按照上述方法转换,
可得:
$ inv(i)=f(i)\times (i-1)!$
即得答案 。
#include<cstdio>
#define ll long long
using namespace std;
ll mul(ll a,ll b,ll mod) //快速幂模板
{
ll ans=1;
while(b)
{
if(b&1) ans=ans*a%mod;
a=(a*a)%mod;
b>>=1;
}
return ans%mod;
}
ll n,p;
ll c[5000010]={1};
ll f[5000010];
int main()
{
scanf("%lld%lld",&n,&p);
for(int i=1;i<=n;i++)
c[i]=(c[i-1]*i)%p;
f[n]=mul(c[n],p-2,p); //获得inv(n!)
for(int i=n-1;i>=1;i--) //递推阶乘的逆元
f[i]=(f[i+1]*(i+1))%p;
for(int j=1;j<=n;j++) //转化并输出
printf("%lld\n",(f[j]*c[j-1])%p);
}
7.扩展中国剩余定理(exCRT)
写在前面:exCRT完全可以求解CRT问题,而由于其优秀性质,可以使模数不互质
给定\(n\)组非负整数\(a_i,b_i\),求解关于\(x\)的方程组的最小非负整数解。
让我们来改变一下格式:
把(1)(2)相减得:
用\(\operatorname{exgcd}\)求解,不能解就无解。
然后我们可以解出一个最小正整数解\(y_1\),带入(1)得到\(x\)其中一个解:
由于我们知道,\(y_1\)的全解,
那么x的全解是
由\(y_1\)的全解可导
即:\(x\equiv x_0(\ mod\ \operatorname{lcm}(a_1,a_2))\)
则:\(x+y_3\operatorname{lcm}(a_1,a_2)=x_0(4)\)
把(3)(4)再联立
即可求解
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int n;
const int maxn = 1e5+7;
ll ai[maxn],bi[maxn];
ll exgcd(ll a,ll b,ll &x,ll &y)
{
if(!b)
{
x=1;
y=0;
return a;
}
ll gcd = exgcd(b,a%b,x,y);
ll p = x;
x = y;
y = p - (a/b)*y;
return gcd;
}
ll mul(ll a,ll b,ll mod)
{
ll res = 0;
while(b > 0)
{
if(b & 1) res = (res+a) % mod;
a = (a + a) % mod;
b>>=1;
}
return res;
}
ll excrt()
{
ll x,y,k;
ll M = ai[1],ans = bi[1];//第一个方程的解特判,分别是模数,等于数
for(int i=2;i<=n;i++)
{
ll a = M,b = ai[i],c = ((bi[i] - ans)%b +b)%b;//ax ≡c(mod b)
ll gcd = exgcd(a,b,x,y),bg = b / gcd;
if(c % gcd != 0) return -1;
x =mul(x , c / gcd , bg);
ans += x * M;//更新前k个方程组的答案
M *= bg;//M为前k个模数的lcm
ans = (ans % M + M) % M;
}
return (ans % M + M) % M;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld%lld",&ai[i],&bi[i]);//模数,乘数
}
printf("%lld",excrt());
return 0;
}
看过代码之后,我们再考虑具体的编程实现问题。
假设已经求出前\(k-1\)个方程组成的同余方程组的一个解为\(x\)
且有\(M=\prod_{i-1}^{k-1}m_i\)
(代码实现中用的就是\(M=LCM_{i-1}^{k-1}m_i\),显然易证这样是对的,还更能防止溢出)
则前\(k-1\)个方程的方程组通解为\(x+i*M(i\in Z)\)
那么对于加入第\(k\)个方程后的方程组
我们就是要求一个正整数t,使得 \(x+t*M \equiv a_k(\mod m_k)\)
转化一下上述式子得 \(t*M \equiv a_k-x(\mod m_k)\)
对于这个式子我们已经可以通过扩展欧几里得求解t
若该同余式无解,则整个方程组无解, 若有,则前k个同余式组成的方程组的一个解解为\(x_k=x+t*M\)
所以整个算法的思路就是求解k次扩展欧几里得
8.关于取模问题
仍要记得开\(\operatorname{long long}\)!!
取模铭记“能取就取”!
基础公式:
一定要记住乘法仍有可能爆\(\operatorname{int}\)
快速幂+取模
可以用分治的方法求快速幂,并且边运行边取模
ll f(ll x,ll y)
{
ll ans=1;
while(y)
{
if(y&1) ans=ans*x%k;
x=x*x%k;
y>>=1;
}
return ans%k;
}
(快速)龟速乘
主要是为了取模
ll mul(ll a,ll b,ll mod)
{
ll res = 0;
while(b > 0)
{
if(b & 1) res = (res+a) % mod;
a = (a + a) % mod;
b>>=1;
}
return res;
}
9.欧拉函数
(1) 基本介绍
\(\phi (n)\)指不超过n并且与n互素的正整数的个数。
\(\phi{(1)} = 1\)
首先我们可以通过容斥原理,我们思考:
给出n唯一分级式\(n=p_1^{r_1}p_2^{r_2}...p_n^{r_n}\)
那么我们应该先从总数n中减去\(p_1,p_2,p_3,...,p_n\)的倍数的个数
即为\(n - \frac{n}{p_1} - \frac{n}{p_1} - \frac{n}{p_1} - ... - \frac{n}{p_n}\)
再加上“同时是两个素因子的倍数的个数”
\(n + \frac{n}{p_1p_2} + \frac{n}{p_1p_3} + \frac{n}{p_2p_3} + ... + \frac{n}{p_{n-1}p_n}\)
再减去“同时是三个素因子的倍数的个数”
一个比较厉害的公式就是
这个这一项 \(\frac{n}{\prod_{p_i\subseteq S}p_i}\) ,前面的符号取决于S中元素的个数,奇数是减法,偶数是加法,由容斥原理可以推出。
下一步有一个不显然的结论:
可以上面公式可以变形为:
或通式:\(\varphi (n)=n\prod\limits_{i=1}^{k}(1-\dfrac{1}{p_i})\),(其中\(p_1,p_2,...,p_k\)为\(n\)的所有质因数)。
这样只需要\(O(n)\)的时间复杂度。
为什么这个式子等价?
展开式子的每一项是从每个括号各选一个(1或$ - \frac{1}{p_i}$),全部加起来再乘以n,就是最初的推倒过程。
举例:
\(\varphi (12)=12 \times (1-\dfrac{1}{2}) \times (1-\dfrac{1}{3})=4\)
(2) 介绍一些定理
定理1:对于\(n=p_1^{a_1}p_2^{a_2}...p_n^{a_n}\),有\(\phi (n)=\phi (p_1^{a_1})\phi (p_2^{a_2})...\phi (p_n^{a_n})\)
定理2:\(p\)为素数,则\(\phi (p)=p-1\).该定理充要。
定理3:\(p\)为素数,\(a\)是正整数,则\(\phi (p^a)=p^a-p^{a-1}=(p-1)p^{a-1}\),因为除了\(p\)的倍数外,其他数都跟\(x\)互质。
定理4:欧拉函数是积性函数,当\(m,n\)为互质,则\(\phi (mn)=\phi (m)\phi (n)\).
定理5:\(p\)为奇数,则\(\phi (2n)=\phi (n)\).
定理6:\(n\)为大于2正整数,则\(\phi (n)\)是偶数.
定理7:\(n\)为正整数,则\(\sum _{d\mid n} \phi(d)=n\).
(3) 求欧拉函数
若没给出唯一分解式,可以通过和质因数分解试除法相似的方法求出。
int euler(int n)
{
int ret=n;
for(int i=2;i*i<=n;i++)
{
if(n%i==0)
{
ret-=ret/i;
while(n%i==0)
{
n/=i;
}
}
}
if(n>1)
ret-=ret/n;
return ret;
}
对于此函数的详细解释可以按照定理3:
由于唯一分解定理,我们一定可以吧一个整数分解为很多素数乘积的形式。
那么对于其中一个素数\(p_i\),我们设\(x = p^k\) ,那么\(\phi (x) = p^{k-1} \times (p - 1)\)
为什么这样?
我们可以吧这个\(x\)分成长度为\(p\) 的\(p^{k-1}\) 段,其中每一段都有 \(p-1\) 个数与\(x\)互质,那么与\(x\)互质的数一共 \(p^{k-1} \times (p - 1)\) 个
由于都是唯一分解定理后,都是素数的乘积,那么可以根据定理4证明所有情况。
为什么n>1直接除?
因为对于质因数分解的形式,\(> \sqrt x\)的最多只有1个质因子。
(4) 筛法求欧拉函数
//筛选法打欧拉函数表
#define Max 1000001
int euler[Max];
void Init(){
euler[1]=1;
for(int i=2;i<Max;i++)
euler[i]=i;
for(int i=2;i<Max;i++)
if(euler[i]==i)
for(int j=i;j<Max;j+=i)
euler[j]=euler[j]/i*(i-1);//先进行除法是为了防止中间数据的溢出
}
10.欧拉定理和费马小定理
欧拉定理
对于任何两个互质的正整数($\ a \bot m\ \() ,且\)a,m(m\geq 2)$
有\(a^{\phi(m)}\equiv 1(\mod m)\)
所以 \(a^b\equiv a^{b\bmod \varphi(m)}\pmod m\)
费马小定理
欧拉定理中\(m\) 为质数时,\(a^{m-1}\equiv 1(\mod m)\)【欧拉定理+欧拉函数定理2】
应用:利用欧拉函数求不超过n且与n互素的正整数的个数,其次可以利用欧拉定理与费马小定理来求得一个逆元,欧拉定理中的m适用任何正整数,而费马小定理只能要求m是质数。
拓展欧拉定理
扩展欧拉定理无需 \(a,m\) 互质。
当 \(a,m\in \mathbb{Z}\) 时有:
原文地址:https://www.luogu.com.cn/blog/asdfo123/shuo-lun-zhuan-ti