https://blog.csdn.net/The_OIer/article/details/106680416
https://www.cnblogs.com/flashhu/p/8324551.html
这一篇是基础内容,具体应用请看这篇。
前置芝士:Splay,文艺平衡树(即下放标记),树链剖分(思想最好会,不过不会也可以)。
1 LCT可以用来解决什么问题
LCT,Link-Cut-Tree。是一种用来解决动态树问题的数据结构。记住LCT不是动态树,只是用来解决动态树问题。
基本操作:
从x连向y一条边
把x到y的边断开
换根
查询路径和(或其它Splay可以维护的东西)
查询连通性相关
......
LCT还有很多套路,后面的应用篇中会提到。
2 实链剖分
LCT维护的实际上是多棵树组成的森林。
对于没课树我们进行实链剖分。
这是一种新的将树剖成链的方法。
类似重链剖分,实链剖分是把树剖成实链和虚链(注意实链和虚链都是树上的链)。
不同的是,实链是我们自己赋予并且可以随意更改的,所以我们需要一种更加灵活的数据结构来维护——Splay。
我们将一棵树剖成实链和虚链,每一条实链上的点都用一棵Splay来维护,关键字是节点的深度。
和重链剖分类似,每个点最多属于一条实链。
3 LCT的性质
很多都已经在实链剖分中提到了。
每一个Splay中序遍历后得到的节点的深度一定是单调递增的(兄弟节点也不能出现)。
边分为实边和虚边,实链通过Splay来维护,而虚边通常是一棵Splay连向另一棵Splay。
具体来讲就是将Splay的根的父亲设为这课Splay深度最小的父亲,但其父亲没有这个儿子(认父不认子)。
放张图片好理解一些:

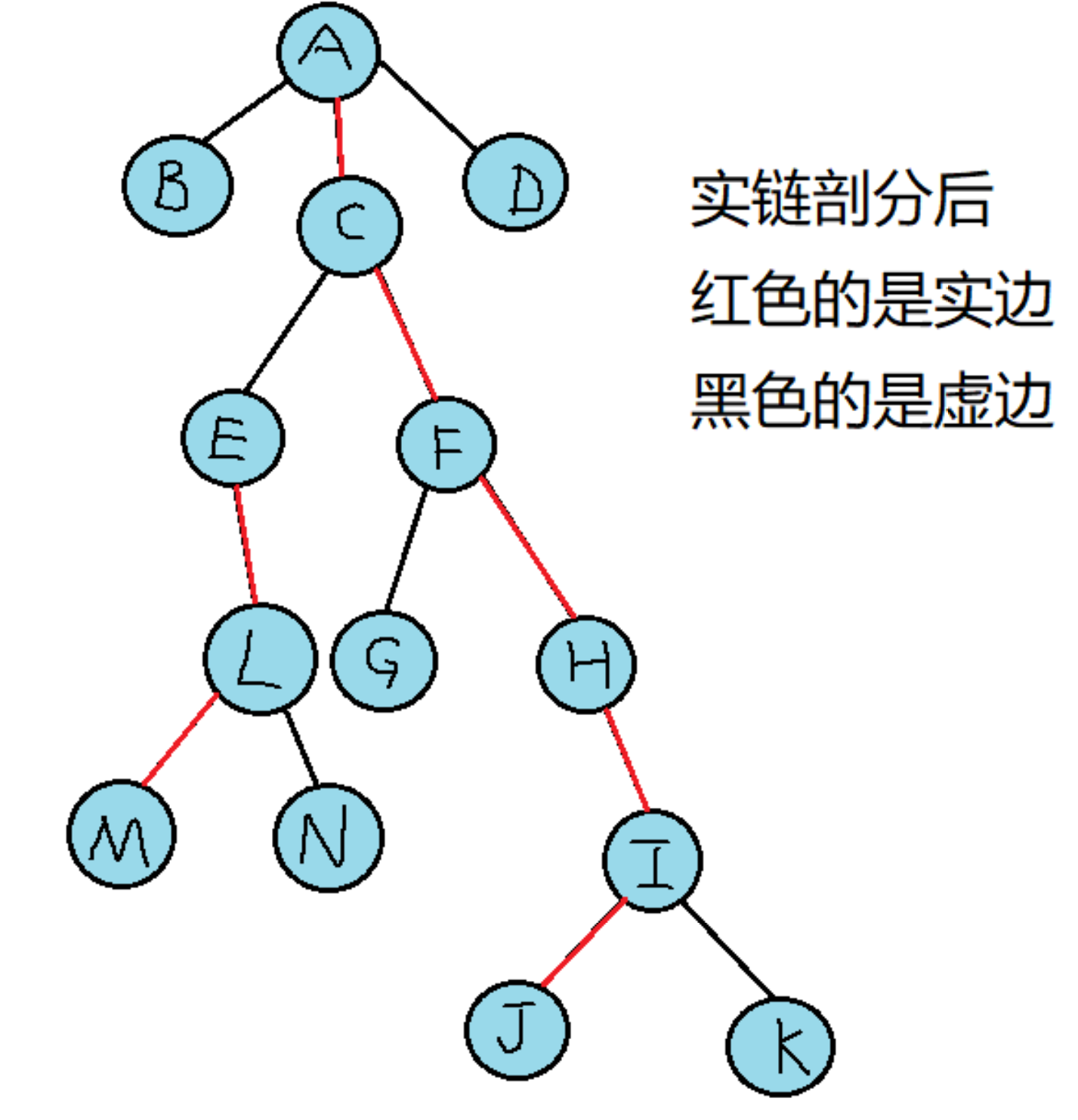
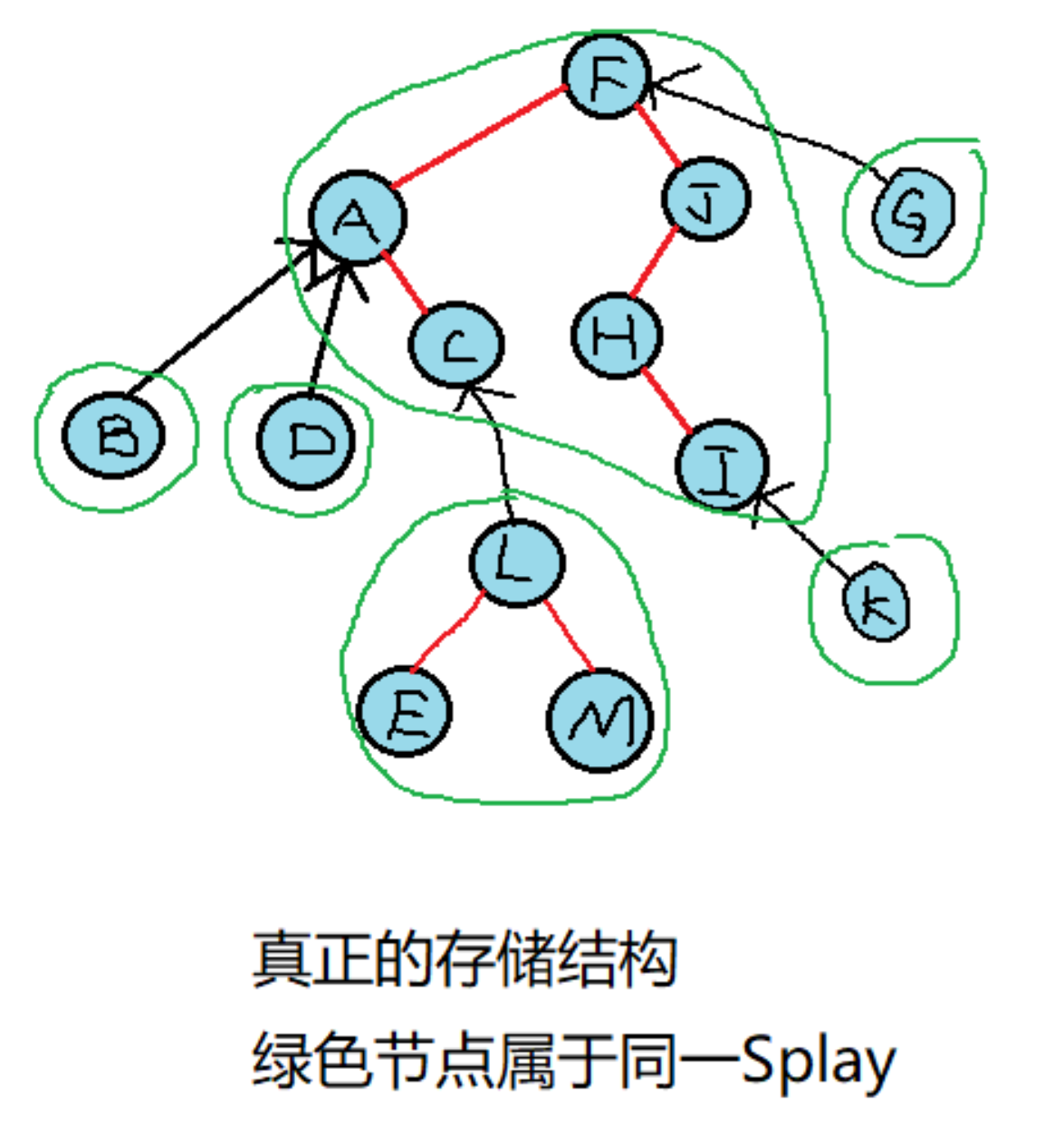
4 LCT的Splay与普通Splay的不同地方
1 根的判断
这里不能用简单的fa=0来判断根,因为它有可能是Splay的根但是它的fa指向另一棵Splay。
那我们可以利用认父不认子的性质来进行判断,就是它的父亲的两个儿子都不是它,那它一定是一棵Splay的根。
代码就一行:
bool is_root(int x) {return son[fa[x]][0] != x && son[fa[x][1] != x;}
2 splay
splay的时候要先把它到根的路径全部都pushdown,而pushdown时一定要从上往下。所以我额外写了一个update函数。
另外lct的splay只需转到根。
inline void update(int x) { if (!is_root(x)) update(fa[x]); push_down(x); } inline void splay(int x) { update(x); for (int f = fa[x]; !is_root(x); rotate(x), f = fa[x]) { if (!is_root(f)) rotate(get(f) == get(x) ? f : x); } push_up(x); }
5 动态树的基本操作的实现
1 access
这算是lct最重要的函数了。
意思是把根到x路径上的边都改为实边。
举个例子:

现在我们要access(N),首先要将N所在的splay深度最小的点也就是L大通其与父亲的虚边,这时为了维护lct的性质,我们需要将I到K的实边变为虚边。
然后就变成了下图:
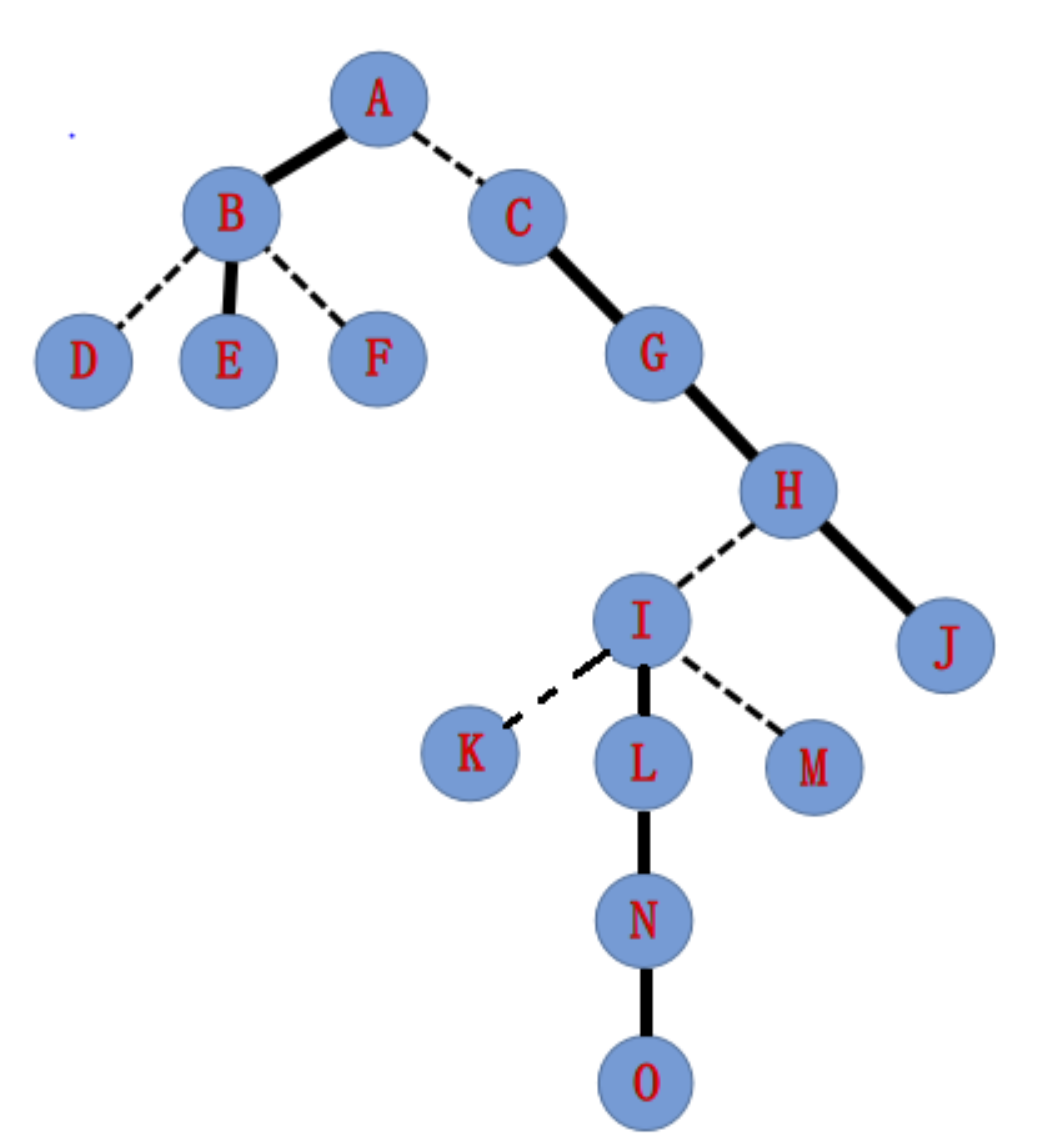
接下来我们要打通H-I的虚边,同上。最后我们会得到下图:
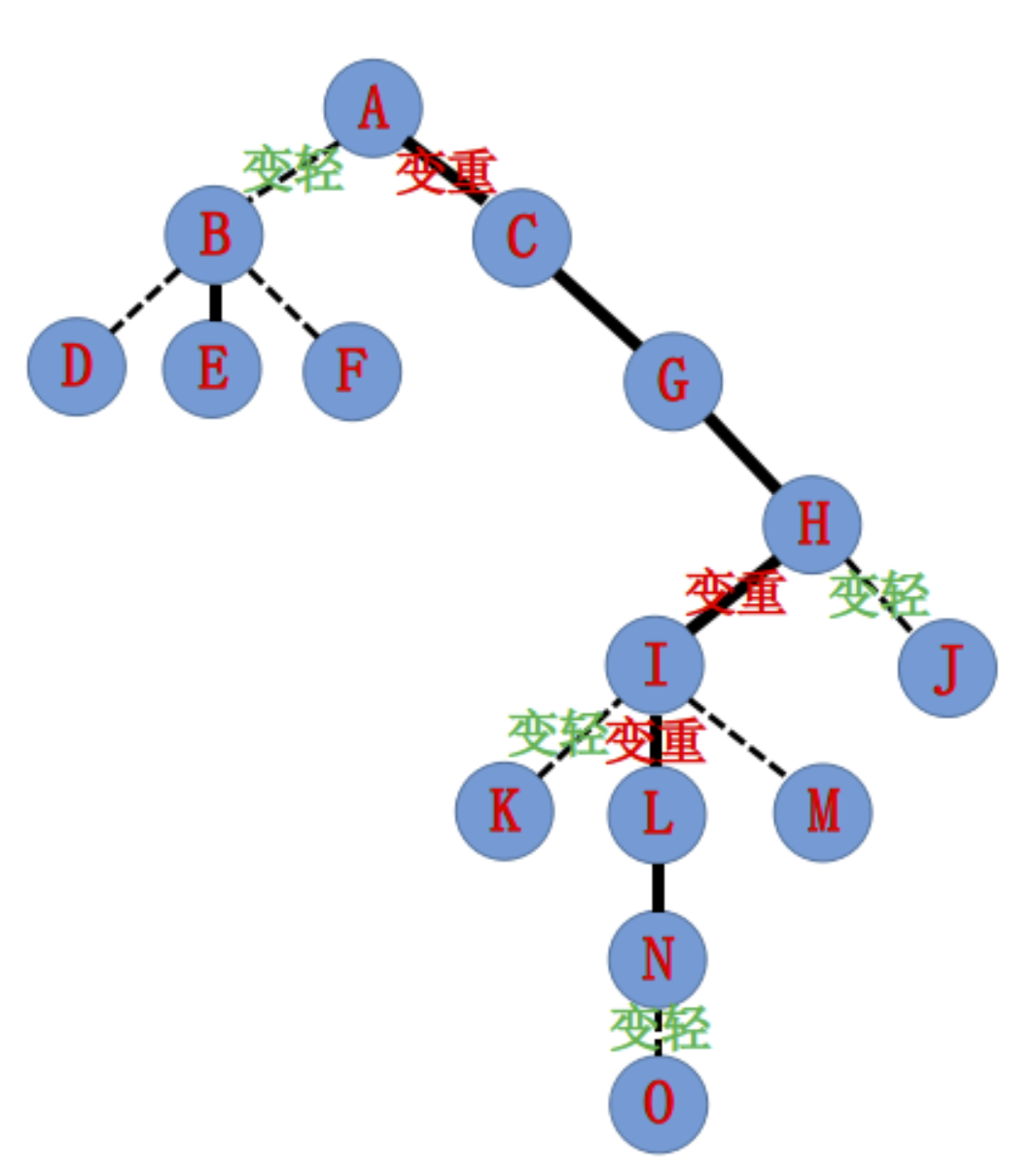
注意到N-O的边也变虚了,那是因为这样代码好写。
具体的代码实现:
void access(int x) { for (int s = 0; x; s = x, f = fa[x]) { splay(x);//先将x splay到当前的根 son[x][1] = s;//将x 的右儿子改为实边 push_up(x);//因为更改了son,所以要记得 pushup } }
2 make_root
make_root就是把某个点设为这棵树的根。
如果将现在从根往下的所有边都变得有向。
将根到x的路径上的边取反即可得到以x为根的一棵树。
所以类似文艺平衡树我们先把x到当前根的路径上的点变为实边,然后将这棵splay打上反转标记即可。
void make_root(int x) { access(x); splay(x); pushr(x); }
3 find_root
find_root是找当前树的根。
通常用来判断连通性。
先将 x 到根的路径打通,然后将 x 旋到根。
其实答案就是深度最小的点,直接找就行。
记得要 pushdown。
void find_root(int x) { access(x); splay(x); while (son[x][0]) push_down(x), x = son[x][0]; splay(x);//为了保证复杂度 return x; }
4 split
拉出x->y的一条链
其实有了上面几个函数也很好写。
先将x变为根,打通y到根的路径,最后将x或y变为根方便后面。
inline void split(int x, int y) { make_root(x); access(y); splay(y); }
5 link
加一条x-y的边
将x变为根,判断y的根是不是x(即判断是否连通)。
如果不连通,将x的父亲设为y即可(认父不认子)。
inline void link(int x, int y) { make_root(x); if (find_root(y) != x) fa[x] = y;//认父不认子 }
6 cut
把原来x-y的边删掉。
如果x-y有边。
那么拉出x到y的链即split(x,y),x必然是y的左儿子,将y的左儿子和x的fa都设为0即可。
那如果没边怎么判断呢?
首先如果y的左儿子不是x则一定不连通,如果x有右儿子则也一定不连通。
inline void cut(int x, int y) { split(x, y); if (son[y][0] == x && !son[x][1]) { son[y][0] = fa[x] = 0; } }
到目前为止所有LCT的基础操作就讲完了,不过LCT绝对不止这些应用,具体可见应用篇。
6 总结
lct维护的是一个森林,每一棵树我们通过是链剖分的方法把树边分为实边和虚边,实链用一棵Splay来维护。
通过一个核心的操作access来实现其它很多操作。