一、SVM
SVM的英文全称是Support Vector Machines,我们叫它支持向量机。支持向量机是我们用于分类的一种算法。
1 示例:
先用一个例子,来了解一下SVM
桌子上放了两种颜色的球,用一根棍分开它们,要求:尽量在放更多球之后,仍然适用。

我们可以这样放:
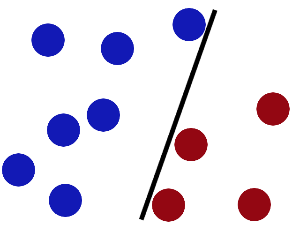
又在桌上放了更多的球,似乎有一个球站错了阵营。显然,我们需要对棍做出调整。
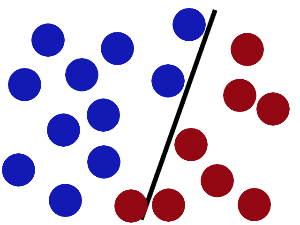
SVM就是试图把棍放在最佳位置,好让在棍的两边有尽可能大的间隙。这个间隙就是球到棍的距离。
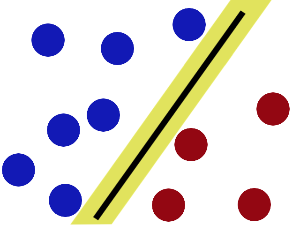
现在好了,即使放了更多的球,棍仍然是一个好的分界线。

现在,加入一个新的挑战:

现在,没有棍可以很好帮他分开两种球了,现在怎么办呢?
我们把桌子一拍,球飞到空中。然后,拿起一张纸,插到了两种球的中间:
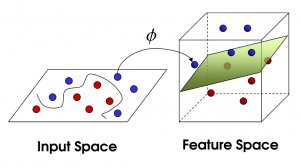
现在,从空中的角度看这些球,这些球看起来像是被一条曲线分开了。
这些球叫做数据(data),棍子叫做分类器(classifier),找到最大间隙的方法(trick)叫做最优化(optimization),拍桌子叫做核函数(kernelling), 那张纸叫做超平面(hyperplane)。
根据刚才的描述,可以看出,问题是从线性可分延伸到线性不可分的。那么,我们就按照这个思路,进行原理性的剖析
2 概述
当一个分类问题,数据是线性可分的,也就是用一根棍就可以将两种小球分开的时候,我们只要将棍的位置放在让小球距离棍的距离最大化的位置即可,寻找这个最大间隔的过程,就叫做最优化。但是,现实往往是很残酷的,一般的数据是线性不可分的,也就是找不到一个棍将两种小球很好的分类。这个时候,我们就需要将小球拍起,用一张纸代替小棍将小球进行分类。想要让数据飞起,我们需要的东西就是核函数(kernel),用于切分小球的纸,就是超平面。
根据刚才的描述,可以看出,问题是从线性可分延伸到线性不可分的。那么,我们就按照这个思路,进行原理性的剖析。
二、线性SVM
先看下线性可分的二分类问题。
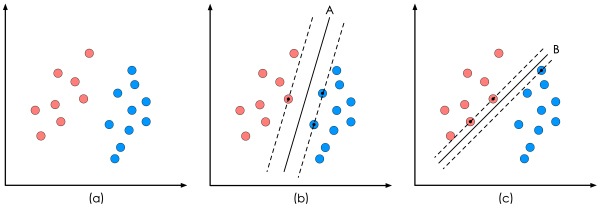
上图中的(a)是已有的数据,红色和蓝色分别代表两个不同的类别。数据显然是线性可分的,但是将两类数据点分开的直线显然不止一条。上图的(b)和(c)分别给出了B、C两种不同的分类方案,其中黑色实线为分界线,术语称为“决策面”。每个决策面对应了一个线性分类器。虽然从分类结果上看,分类器A和分类器B的效果是相同的。但是他们的性能是有差距的,看下图:
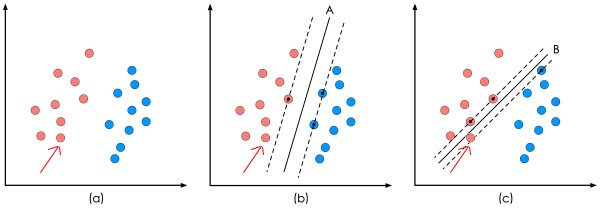
在"决策面"不变的情况下,我又添加了一个红点。可以看到,分类器B依然能很好的分类结果,而分类器C则出现了分类错误。显然分类器B的"决策面"放置的位置优于分类器C的"决策面"放置的位置,SVM算法也是这么认为的,它的依据就是分类器B的分类间隔比分类器C的分类间隔大。这里涉及到第一个SVM独有的概念"分类间隔"。在保证决策面方向不变且不会出现错分样本的情况下移动决策面,会在原来的决策面两侧找到两个极限位置(越过该位置就会产生错分现象),如虚线所示。虚线的位置由决策面的方向和距离原决策面最近的几个样本的位置决定。而这两条平行虚线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。两条虚线之间的垂直距离就是这个最优决策面对应的分类间隔。显然每一个可能把数据集正确分开的方向都有一个最优决策面(有些方向无论如何移动决策面的位置也不可能将两类样本完全分开),而不同方向的最优决策面的分类间隔通常是不同的,那个具有“最大间隔”的决策面就是SVM要寻找的最优解。而这个真正的最优解对应的两侧虚线所穿过的样本点,就是SVM中的支持样本点,称为"支持向量"。
1 数学建模
求解这个"决策面"的过程,就是最优化。一个最优化问题通常有两个基本的因素:1)目标函数,也就是你希望什么东西的什么指标达到最好;2)优化对象,你期望通过改变哪些因素来使你的目标函数达到最优。在线性SVM算法中,目标函数显然就是那个"分类间隔",而优化对象则是决策面。所以要对SVM问题进行数学建模,首先要对上述两个对象("分类间隔"和"决策面")进行数学描述。按照一般的思维习惯,我们先描述决策面。
数学建模的时候,先在二维空间建模,然后再推广到多维。
1)"决策面"方程
我们都知道二维空间下一条直线的方式如下所示:
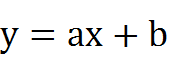
现在我们做个小小的改变,让原来的x轴变成x1,y轴变成x2
移项得:
将公式向量化得:
进一步向量化,用w列向量和x列向量和标量γ进一步向量化:
其中,向量w和x分别为:
这里w1=a,w2=-1。我们都知道,最初的那个直线方程a和b的几何意义,a表示直线的斜率,b表示截距,a决定了直线与x轴正方向的夹角,b决定了直线与y轴交点位置。那么向量化后的直线的w和r的几何意义是什么呢?
现在假设:
可得:
在坐标轴上画出直线和向量w
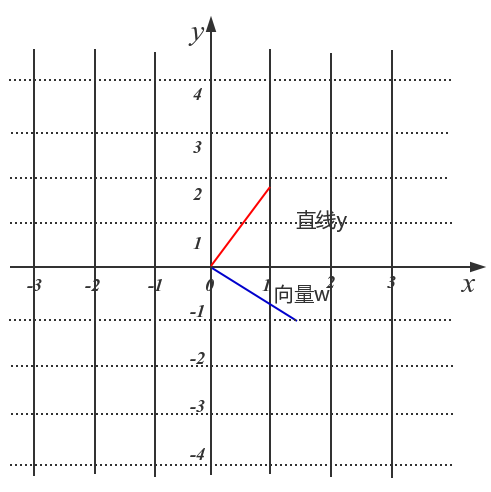
蓝色的线代表向量w,红色的线代表直线y。我们可以看到向量w和直线的关系为垂直关系。这说明了向量w也控制这直线的方向,只不过是与这个直线的方向是垂直的。标量γ的作用也没有变,依然决定了直线的截距。此时,我们称w为直线的法向量。
二维空间的直线方程已经推导完成,将其推广到n维空间,就变成了超平面方程。(一个超平面,在二维空间的例子就是一个直线)但是它的公式没变,依然是:
不同之处在于:
我们已经顺利推导出了"决策面"方程,它就是我们的超平面方程,之后,我们统称其为超平面方程。
2)"分类间隔"方程
现在,我们依然对于一个二维平面的简单例子进行推导。
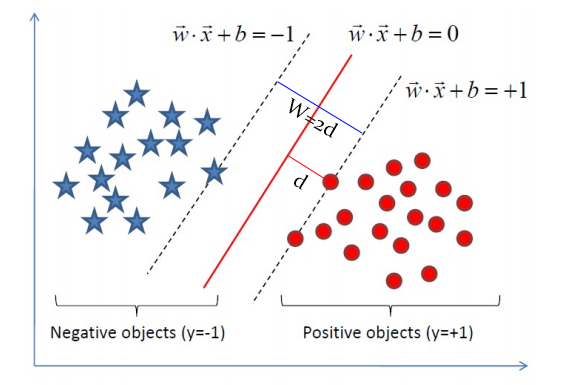
我们已经知道间隔的大小实际上就是支持向量对应的样本点到决策面的距离的二倍。那么图中的距离d我们怎么求?我们高中都学过,点到直线的距离距离公式如下:
公式中的直线方程为Ax0+By0+C=0,点P的坐标为(x0,y0)。
现在,将直线方程扩展到多维,求得我们现在的超平面方程,对公式进行如下变形:
这个d就是"分类间隔"。其中||w||表示w的二范数,求所有元素的平方和,然后再开方。比如对于二维平面:
那么,
我们目的是为了找出一个分类效果好的超平面作为分类器。分类器的好坏的评定依据是分类间隔W=2d的大小,即分类间隔w越大,我们认为这个超平面的分类效果越好。此时,求解超平面的问题就变成了求解分类间隔W最大化的为题。W的最大化也就是d最大化的。
3)约束条件
看起来,我们已经顺利获得了目标函数的数学形式。但是为了求解w的最大值。我们不得不面对如下问题:
- 我们如何判断超平面是否将样本点正确分类?
- 我们知道要求距离d的最大值,我们首先需要找到支持向量上的点,怎么在众多的点中选出支持向量上的点呢?
上述我们需要面对的问题就是约束条件,也就是说我们优化的变量d的取值范围受到了限制和约束。事实上约束条件一直是最优化问题里最让人头疼的东西。但既然我们已经知道了这些约束条件确实存在,就不得不用数学语言对他们进行描述。但SVM算法通过一些巧妙的小技巧,将这些约束条件融合到一个不等式里面。
这个二维平面上有两种点,我们分别对它们进行标记:
- 红颜色的圆点标记为1,我们人为规定其为正样本;
- 蓝颜色的五角星标记为-1,我们人为规定其为负样本。
对每个样本点xi加上一个类别标签yi:
如果我们的超平面方程能够完全正确地对上图的样本点进行分类,就会满足下面的方程:
如果我们要求再高一点,假设决策面正好处于间隔区域的中轴线上,并且相应的支持向量对应的样本点到决策面的距离为d,那么公式进一步写成:
上述公式的解释就是,对于所有分类标签为1和-1样本点,它们到直线的距离都大于等于d(支持向量上的样本点到超平面的距离)。公式两边都除以d,就可以得到:
其中,
因为||w||和d都是标量。所以上述公式的两个矢量,依然描述一条直线的法向量和截距。
上述两个公式,都是描述一条直线,数学模型代表的意义是一样的。现在,让我们对wd和γd重新起个名字,就叫它们w和γ。因此,我们就可以说:"对于存在分类间隔的两类样本点,我们一定可以找到一些超平面,使其对于所有的样本点均满足下面的条件:"
上述方程即给出了SVM最优化问题的约束条件。这时候,可能有人会问了,为什么标记为1和-1呢?因为这样标记方便我们将上述方程变成如下形式:
正是因为标签为1和-1,才方便我们将约束条件变成一个约束方程,从而方便我们的计算。
4)线性SVM优化问题基本描述
现在整合一下思路,我们已经得到我们的目标函数:
我们的优化目标是是d最大化。我们已经说过,我们是用支持向量上的样本点求解d的最大化的问题的。那么支持向量上的样本点有什么特点呢?
现在我们就可以将我们的目标函数进一步化简:
因为,我们只关心支持向量上的点。随后我们求解d的最大化问题变成了||w||的最小化问题。进而||w||的最小化问题等效于
为什么要做这样的等效呢?这是为了在进行最优化的过程中对目标函数求导时比较方便,但这绝对不影响最优化问题最后的求解。我们将最终的目标函数和约束条件放在一起进行描述:
这里n是样本点的总个数,缩写s.t.表示"Subject to",是"服从某某条件"的意思。上述公式描述的是一个典型的不等式约束条件下的二次型函数优化问题,同时也是支持向量机的基本数学模型。
5)求解准备





















