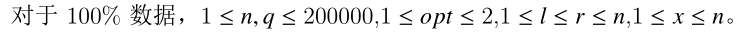神奇的集合 [set维护区间, 线段树]

$神奇的集合$

---

$color{red}{正解部分}$

因为 $1 le x le n$, 所以可以对每个 $x$ 使用 std::set< std::pair<int, int> > 存储其出现的区间, 线段树 维护答案,

• 对 $1$ 操作, 如图所示, 黄色为修改的区间, 黑色为原有的 $x$ 出现的区间, 相交部分使用红线标出,
  第一次出现的区间在 线段树 中 $+1$, 已经出现过的区间在 线段树 中 $imes 2$ .
  
  每次操作后合并区间 .

• 对 $2$ 操作, 直接在 线段树 中查询即可 .

时间复杂度 $O(n log n)$ .

---

$color{red}{实现部分}$

#include<bits/stdc++.h>
#define reg register
#define fi first
#define se second
typedef std::pair <int, int> pr;
typedef long long ll;

int read(){
        char c;
        int s = 0, flag = 1;
        while((c=getchar()) && !isdigit(c))
                if(c == '-'){ flag = -1, c = getchar(); break ; }
        while(isdigit(c)) s = s*10 + c-'0', c = getchar();
        return s * flag;
}

const int maxn = 200005;
const int mod = 998244353;

int N;
int q;

std::set <pr> st[maxn];
std::set <pr>::iterator it_1, it_2, ptk[maxn];

struct Segment_Tree{

        struct Node{ int l, r; ll v, tag, cf; } T[maxn<<3];

        void Build(int k, int l, int r){
                T[k].l = l, T[k].r = r, T[k].cf = 1;
                if(l == r) return ;
                int mid = l+r >> 1;
                Build(k<<1, l, mid), Build(k<<1|1, mid+1, r);
                Push_up(k);
        }

        void Push_up(int k){ T[k].v = (T[k<<1].v + T[k<<1|1].v) % mod; }

        void Push_down(int k){
                T[k].v = T[k].cf * T[k].v % mod;
                T[k].v += (T[k].r-T[k].l+1)*T[k].tag, T[k].v %= mod;
                int lt = k<<1, rt = k<<1|1;
                (T[lt].cf *= T[k].cf) %= mod, (T[rt].cf *= T[k].cf) %= mod;
                (T[lt].tag *= T[k].cf) %= mod, (T[rt].tag *= T[k].cf) %= mod;
                (T[lt].tag += T[k].tag) %= mod, (T[rt].tag += T[k].tag) %= mod;
                T[k].tag = 0, T[k].cf = 1;
        }

        void Modify(int k, const int &ql, const int &qr, int aim){
                int l = T[k].l, r = T[k].r;
                if(T[k].tag || T[k].cf != 1) Push_down(k);
                if(r < ql || l > qr) return ;
                if(ql <= l && r <= qr){ (T[k].tag += aim) %= mod; Push_down(k); return ; }
                int mid = l+r >> 1;
                Modify(k<<1, ql, qr, aim), Modify(k<<1|1, ql, qr, aim);
                Push_up(k);
        }

        void Todify(int k, const int &ql, const int &qr, int aim){
                int l = T[k].l, r = T[k].r;
                if(T[k].tag || T[k].cf != 1) Push_down(k);
                if(r < ql || l > qr) return ;
                if(ql <= l && r <= qr){ (T[k].tag *= aim) %= mod; (T[k].cf *= aim) %= mod; Push_down(k); return ; }
                int mid = l+r >> 1;
                Todify(k<<1, ql, qr, aim), Todify(k<<1|1, ql, qr, aim);
                Push_up(k);
        }

        ll Query(int k, const int &ql, const int &qr){
                int l = T[k].l, r = T[k].r; 
                if(T[k].tag || T[k].cf != 1) Push_down(k);
                if(r < ql || l > qr) return 0;
                if(ql <= l && r <= qr) return T[k].v;
                int mid = l+r >> 1;
                return (Query(k<<1, ql, qr) + Query(k<<1|1, ql, qr)) % mod;
        }

} seg_t;

void Work(){
        int opt = read(), l = read(), r = read();
        if(opt == 1){
                int x = read();
                if(st[x].empty()) st[x].insert(pr(l, r)), seg_t.Modify(1, l, r, 1);
                else{
                        seg_t.Modify(1, l, r, 1);
                        int Llim = l, Rlim = r, cnt = 0;
                        it_1 = st[x].lower_bound(pr(l, l));
                        if(it_1 != st[x].begin()){
                                it_2 = it_1; it_2 --;
                                if(it_2->se >= l){
                                        int lm = l, rm = std::min(r, it_2->se);
                                        seg_t.Modify(1, lm, rm, -1), seg_t.Todify(1, lm, rm, 2);
                                        Llim = std::min(Llim, it_2->fi), Rlim = std::max(Rlim, it_2->se);
                                        ptk[++ cnt] = it_2;
                                }
                        }

                        for(; it_1 != st[x].end() && it_1->fi <= r; it_1 ++){
                                int lm = it_1->fi, rm = std::min(it_1->se, r);
                                seg_t.Modify(1, lm, rm, -1), seg_t.Todify(1, lm, rm, 2);
                                Llim = std::min(Llim, it_1->fi), Rlim = std::max(Rlim, it_1->se);
                                ptk[++ cnt] = it_1;
                        }
                        for(reg int i = 1; i <= cnt; i ++) st[x].erase(ptk[i]);
                        st[x].insert(pr(Llim, Rlim));
                }
        }else printf("%lld
", seg_t.Query(1, l, r));
}

int main(){
        N = read(), q = read();
        seg_t.Build(1, 1, N);
        while(q --) Work();
        return 0;
}