转载请标明出处:http://www.cnblogs.com/zblade/
一、概要
在项目开发中,有引入用到rANS熵编码压缩算法,在使用的背后,想看看其运行的基本原理,也算补一下个人的熵编码知识。这里提到的熵编码压缩算法都是无损压缩。很久没有写文章了,太忙了,不知道一年一篇文章算不算年更 :b
二、熵编码
目前较为成熟的熵编码是霍夫曼编码,算术编码,以及14年Duda提出的ANS(Asymmetric Numeral Systems 非对称数系)编码。先解释一下霍夫曼编码和算术编码,然后重点说一下ANS编码的原理。
2.1 香农熵编码
熵在编码中,是对信息的衡量,熵越大,表明所包含的信息越多。对于高频出现的事件,其本身包含的信息其实是不多的,所以其对应的熵更小。而低频出现的事件,其包含的信息更多,对应的熵更大。香农的熵编码理论值计算公式为: ...(1)
2.2 霍夫曼编码
霍夫曼编码是速度最快的熵编码,其基本原理是基于统计的频率,构建二叉树,最后高频率的字符用最短的编码表示,最低频率的字符用最长的编码来表示。其基本的操作就是不断构建二叉树的过程,借鉴示例用图1:
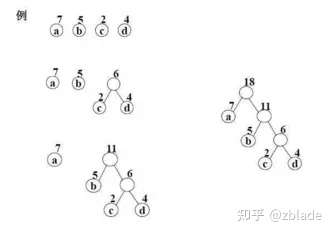
基本操作就是取频率最低的2个字符,搭建一颗二叉树,然后根节点频率为叶子节点之和,如此递归,得到最终的二叉树,示例中的编码结果:
a: 0
b: 10
c: 110
d: 111用编码替换输入的字符,即可得到最终的编码结果。 霍夫曼编码总结就是2个操作:构建霍夫曼树,执行霍夫曼编码。霍夫曼是执行速度最快的熵编码,但是其不能无限接近熵编码的理论值。
2.3 算术编码
算术编码是一种无限接近熵编码理论值的编码,其本质操作就是用一个[0, 1)的小数来表示最终的编码结果,其基本操作也是基于统计来进行的,用示例图来表示最直观[2]:
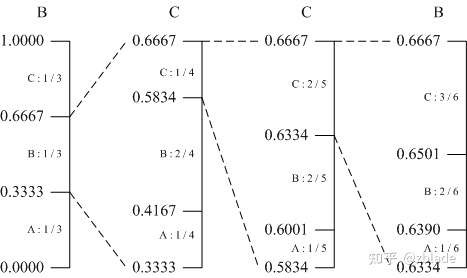
当前编码的字符为ABC三种字符,如何编码“BCCB”这个字符?
1)设定初始频率值,三种字符均值分布,则均为1/3,划分初步的概率分布;
2)输入B,其位于[0.333,0.667),则以此区间进行下一次划分,这是各个字符出现的频率进行更新,分别为1/4, 2/4, 1/4,得到最新的区间划分;
3)依次递推,最后编码所在区间为[0.639,0.6501),输出这个区间内的一个小数,例如0.64,转换为对应的二进制数即为最终的编码结果。 算术编码是一种能够接近理论值的熵编码,对应的代价就是算术的过程,速度慢。
三、ANS熵编码
项目中用到的编码是最近几年提出的一种新的熵编码,本着查看原理的心理去探究了一下这种最新的编码,很多文章都说的较为晦涩,不是我这样的小白能够理解的。在偶然拜读到一位国外大佬的文章后,通过详细的推导,总算大致了解了基本的实现原理,这里推荐有时间的可以看这篇英文原文:
Lossless Compression with Asymmetric Numeral Systems 结合这篇文章,我大致讲讲个人的理解:
3.1 将二进制字符串编码成自然数
从最简单的编码开始,假设一个字符串是以0/1字符串组成,如果用进制转换,我们都知道如何将其转换为10进制数。让我们展开来看:
假设我们已经转换了二进制字符串, 其对应的数值为
,如果我们得到一个新的输入字符
,我们希望基于一个基本的编码函数来得到输出的数值,假设为:
....(2)
基于离散数学教程,如果还记得的话,这个公式是这样: ...(3)
为了区别"0"、“00”等情况,我们设定初始值:, 反过来,我们可以从一个10进制数转换成对应的二进制字符串,其对应的函数可以表示为:
...(4)
举例来说明:
基于公式3和4,将字符转换成一个十进制数,
, 那么其转换操作为:
其对应的解码过程为:
最终“10011”二进制字符串,转换为十进制数为51,需要用个bit来表示,相对于理论极限值,多了一位,注意这里的解压结果相对输入字符串是倒序的,一般应用的时候,会先将输入倒序排列,这样解压得到结果就是正序的结果。
3.2 编码函数推导
上面的编码都是基于0和1字符串是均值分布的前置条件的,实际情况中,是很大可能出现不均值分布的情况的。
引用前面的公式2,, 假设
具有
位的信息,如果我们想把
用理论值编码
位信息,那么可以推导公式:
所以:
所以,我们可以得到这样的理论编码函数: ...(5)
3.3 Uniform Binary Variant(uABS)
现在我们将范围拓展,假设我们要编码的数字范围为[1,N], 用"1" 和"0"来分别表示奇数和偶数,对应的概率为 和
, 对应的在N个数字中,偶数出现的次数为
, 那么我们可以推导N+1 和 N之间的关系为:
...(6)
这里就不再详细的推证了,公式6等价于:...(7)
基于公式7,我们就可以依次编码非均值分布的二进制数字符串了,其对应的解码公式为: =>
用实例来演示编码和解码的过程:
继续上面的用例, 设定
,其编码过程为:
对应的解码过程为:
3.4 Range Variant(rANS)
上面的uABS是针对二进制字符的熵编码,我们也可以进一步的推广到非二进制字符的非均值熵编码。首先我们需要明确的是,公式5是依然生效的,只是在推广的时候,我们将推广为
,也就是输入的二进制字符变成符号
即可。这样在新增一个字符的时候,对应的等价新增该字符的熵编码信息,所以公式5是依然生效的。
此外理论上来说,对于字符集,我们是可以有任意的概率分布的(只要字符集任意长),但是实际的时候我们是将其限定在一个量化范围内的,一般是的范围。在这个范围内,符号
出现的次数为
,那么可以得到
, 基于这个量化,结合uABS的公式,可以用下面的公式来表示rANS的编码:
...(8)
对应的解码操作公式为:....(9)
...(10)
其中,可以理解为累计分布统计操作。
用示例来解释一下压缩和解压:
对于字符集['a', 'b', 'c'],其量化的 n = 3, 其统计的分布为, 其对应的
, 现在我们来编码字符串"abc",对于初始值
, 我们设定为
,基于公式8可以得到编码过程为:
对应的解码操作为:
3.5 量化处理rANS
上面的rANS编码展示的是短字符的时候的编码流程,如果一个文件大小有1MB或者更大,这么长的字符串如何编码?如果直接编码的话,肯定会超过整数的表示范围,解决办法就是移位分解:
当编码的时候,得到的结果过大时,将其右移M位来确保得到的结果处于
(例如M= 16bits)这个区间,同理在解压的时候,如果
较小,会将其左移M位,然后在进行处理,这样就能确保编码结果能用整形数来表示,其大致操作流程为:
MASK = 2**M -1
BOUND = 2**(2*M) - 1
##Encoding
s = readsymbol()
x_test = (x / f[s]) << n + (x % f[s]) + c[s]
if(x_test > BOUND):
write16bits(x & MASK)
x = x >> M
x = (x /f[s]) << n + (x % f[s]) + c[s]
##Decoding
s = symbol[x & MASK]
writeSymbol(s)
x = f[s](x >> n) + (x & MASK) -c[s]
if(x < 2**M):
x = x << M + read16bits()对于ANS, 还有其他的编码,例如tANS编码,这里就不再讨论,还没看到这部分的编码。在实际的编码过程中,就是脱胎于上面的编码理论,进一步的完善编码上下文内容即可。
引用:
[1]:熵压缩:信息熵、Huffman编码、算数编码、ANS+FSE
[2]:算术编码_小石_新浪博客