Part 1:什么是Trie树
当然叫它Trie(踹)树不是让你真的去踹它
Trie;,又称单词查找树,是一种树形结构,用于保存大量的字符串。它的优点是:利用字符串的公共前缀来节约存储空间。
它的本质是一棵(k)叉树((k)取决于构成字符串的字符种类)
Part 2:Trie树建立和查询
Trie树的建立
为了方便理解,我们用图来表示一颗Trie树建立的过程

最初,Trie树中只有一个根节点root
假设我们插入字符串001,那么Trie就变成了这样(因为Graph Editor不支持相同名字的节点,我就只能回归手绘了)
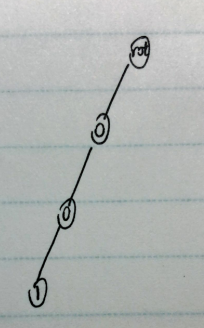
再次插入字符串011,因为他们有一个公共前缀0,此时不需要再在根节点建一个0儿子,所以Trie变成了这样:
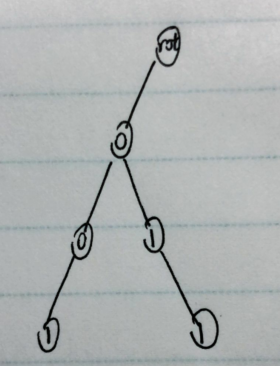
再插入字符串100,因为根节点没有1儿子,新建之
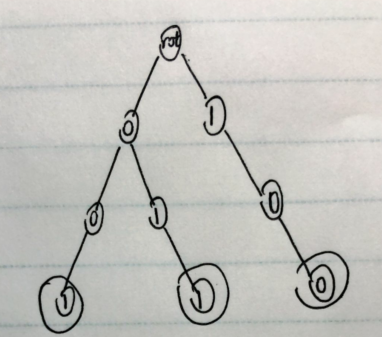
注:标记圆圈的是字符串的末尾
所以Trie就的插入操作的本质就是:
在父节点检查有没有匹配下一个字符的儿子,如果有,就进入这个匹配的儿子继续寻找下一个字符,如果没有就给它新建一个匹配的节点,继续寻找
一直重复直到整个字符串被插入到Trie树中即可,别忘了在字符串结尾处打上标记!
Trie树的查询
首先明确,Trie帮助我们做的事是查询在已经给出的字典中,有几个是给定字符串的前缀
那么我们从根节点开始按照给定字符串在Trie中扫描,如果给定字符串的下一个字符在Trie树中有匹配的儿子节点,那么指针跳到这个儿子节点,同时检查这里是不是一个字符串的末尾,如果是,那么答案+1
如果给定的字符串的下一个字符在当前节点中没有匹配的儿子节点,说明在字典中这一位字符没有和给定字符串的这一位相同的,那么之后的字符串都不可能是给定字符串的前缀,直接返回答案即可
比如查询上面那棵Trie树中有几个字符串是00100的前缀
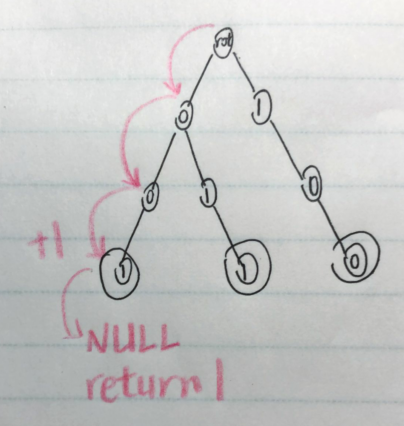
具体的步骤:rot->找到0->跳到0->找到0->跳到0->找到1->跳到1->1是一个字符串的末尾->答案+1->找不到0->返回答案1
假设有一个字符串是0,也在字典树中,那么对于字符串00100的查询就是这样的:

rot->找到0->0是一个字符串的末尾->答案+1->找到0->跳到0->找到1->跳到1->1是一个字符串的末尾->答案+1->找不到0->返回答案2
Part 3: 如何优美的写出一珂Trie树
emmmm,大部分人们喜欢使用数组写数据结构,但是窝不太一样……
既然是树形结构,窝自然的想到了一扶苏一dalao教我的指针线段树写法
线段树是二叉树,搞了两个指针ls,rs,那么类比一下,Trie树是k叉树,就搞k个指针
搞一个根节点rot,然后每次插入的时候,从根节点找到匹配的儿子就往下跳,没有匹配的就用new新建节点再跳
查询也同理,从rot往下查询,找到就往下跳,统计v,没找到就返回答案
于是这么一珂奇奇怪怪的Trie就出炉了
struct Trie{
int v;//记录是几个字符串的结尾(有可能有相同的字符串在字典中)
Trie *nxt[15];//假设是数字串,表示0-9,多开一点无所谓,nxt[i]表示儿子字符i
Trie(){//搞一个构造函数用来初始化
v=0;
for(int i=0;i<Max;i++)
nxt[i]=NULL;
}
};
Trie *rot=new Trie;//申请一个根节点
inline void insert(char *str){//插入操作
int len=strlen(str);//统计字符串长度
Trie *p=rot,*q;//从根节点开始建立
for(int i=0;i<len;i++){
int it=str[i]-'0';
if(p->nxt[it]==NULL){//没有儿子str[i]
p->nxt[it]=new Trie;//没有就建一个
p=p->nxt[it];//跳下去
}else p=p->nxt[it];//有就直接跳
}
p->v++;//记录下最后一个节点是一个字符串的末尾
}
inline int query(char *str){
int ans=0; //有ans个前缀
int len=strlen(str);
Trie *p=rot;//从根节点开始跳
for(int i=0;i<len;i++){
int it=str[i]-'0';
p=p->nxt[it];//先跳到下一个字符
if(p==NULL)//如果并没有这个字符,返回ans
return ans;
ans+=p->v;//有,那么答案+p->v
}
return ans;//返回答案
}
Part 4:使用Trie树切题
其实洛谷上的某些关于Trie树的题存在恶意评价难度的现象,但是那跟我们这些蒟蒻无关
我们只需要享受用Trie的板子稍微改一改就切绿切蓝的快乐就好了
UVA11362 Phone List
传送门与标签
传送门:UVA11362 Phone List
双倍经验:UVA644 Immediate Decodability
双倍经验AC代码
标签:Trie,字典树
(Solution)
题目中给定一堆字符串,问我们其中是不是有字符串A,B满足A是B的前缀或B是A的前缀
那么我们只需要每次读入一个字符串,然后先在字典树中查询有没有字符串是它的前缀
如果没有,把这个字符串插入字典树,继续操作,直到到了数据结束或者找到前缀字符串
(Code)
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<algorithm>
#include<set>
#include<map>
#include<utility>
#include<iostream>
#include<list>
#include<ctime>
#include<cmath>
#include<cstdlib>
#include<iomanip>
typedef long long int ll;
inline int read(){
int fh=1,x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-') fh=-1;ch=getchar(); }
while('0'<=ch&&ch<='9'){ x=(x<<3)+(x<<1)+ch-'0';ch=getchar(); }
return fh*x;
}
inline int _abs(const int x){ return x>=0?x:-x; }
inline int _max(const int x,const int y){ return x>=y?x:y; }
inline int _min(const int x,const int y){ return x<=y?x:y; }
inline int _gcd(const int x,const int y){ return y?_gcd(y,x%y):x; }
inline int _lcm(const int x,const int y){ return x*y/_gcd(x,y); }
using namespace std;
#define Max 15
int n,t;
struct Trie{
int v;
Trie *nxt[15];
Trie(){
v=1;
for(int i=0;i<Max;i++)
nxt[i]=NULL;
}
};
Trie *rot=new Trie;
void createTrie(char *str){//同上的模板化插入
int lenth=strlen(str);
Trie *p=rot;
for(int i=0;i<lenth;i++){
int id=str[i]-'0';
if(p->nxt[id]==NULL){
p->nxt[id]=new Trie;
p=p->nxt[id];
}else{
p->v++;
p=p->nxt[id];
}
}
p->v=-1;
}
int findTrie(char *str){
int lenth=strlen(str);
Trie *p=rot;
for(int i=0;i<lenth;i++){
int id=str[i]-'0';
p=p->nxt[id];
if(p==NULL)
return 0;//没找到下一个字符儿子,返回0
if(p->v==-1)
return -1;//有一个字符串是这个字符串的前缀
}
return 1;//这个字符串是别的字符串的前缀
}
int main(){
t=read();
while(t--){
n=read();
bool flag=true;
rot=new Trie;//重置Trie树
for(int i=0;i<n;i++){
char st[Max];
scanf("%s",st);
int ans=findTrie(st);
createTrie(st);
if(ans==-1||ans==1) flag=false;
}
if(flag==false) printf("NO
");//找到了前缀串,输出答案
else printf("YES
");
}
return 0;
}
洛谷P2922 [USACO08DEC]Secret Message G
标签与传送门
传送门:洛谷P2922 [USACO08DEC]Secret Message G
标签:Trie,字典树
(Solution)
给出包含n个单词的字典,有m次查询,每次查询给出一个字符串A,求出字典中多少个字符串与A有相同前缀
注意这个相同前缀指的是:字典中的串B是A的前缀或者A是B的前缀
还是先建立字典树,记录当前节点是几个单词的公共前缀m,是几个单词的结尾v
每次查询从根节点向下,有两种情况:
1、如果查询串中第i个字符在字典树中找不到,那么这个查询串就不可能是任何字典树中字符串的前缀
这样就只用考虑字典树中字符串有几个是查询串的前缀即可,显然,可以累加维护(sum v),如果找不到,直接返回(sum v)即可
2、在字典树中从根向下可以找到完整的查询串,那么这个查询串不仅在字典树中有(sum v)个字符串是它的前缀,而它本身也是m个字典树中字符串的前缀
那么我们不光要记录(sum v),还要找到查询串的最后一个单词所在的节点是几个字典树中单词的公共前缀m,m+v得到答案
注意最后要减掉以最后一个点为结尾的字典中字符串的数量,因为这部分字符串不仅算了v,也算了m,所以要去掉重复,做到不重不漏
(Code)
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<algorithm>
#include<set>
#include<map>
#include<utility>
#include<iostream>
#include<list>
#include<ctime>
#include<cmath>
#include<cstdlib>
#include<iomanip>
typedef long long int ll;
inline int read(){
int fh=1,x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-') fh=-1;ch=getchar(); }
while('0'<=ch&&ch<='9'){ x=(x<<3)+(x<<1)+ch-'0';ch=getchar(); }
return fh*x;
}
inline int _abs(const int x){ return x>=0?x:-x; }
inline int _max(const int x,const int y){ return x>=y?x:y; }
inline int _min(const int x,const int y){ return x<=y?x:y; }
inline int _gcd(const int x,const int y){ return y?_gcd(y,x%y):x; }
inline int _lcm(const int x,const int y){ return x*y/_gcd(x,y); }
using namespace std;
#define Max 15
#define maxn 10005
struct Trie{
int w,v;//w表示这个节点是几个字符串的公共前缀的末尾,v表示有几个字符串以这个节点为结尾
Trie *nxt[Max];
Trie(){
w=1,v=0;//w初始化为1,v初始化为0
for(int i=0;i<Max;i++)
nxt[i]=NULL;
}
};
Trie *rot=new Trie;
inline void createTrie(int *str,int lenth){
Trie *p=rot;
for(int i=0;i<lenth;i++){
int id=str[i];
if(p->nxt[id]==NULL){
p->nxt[id]=new Trie;//新开节点再往下跳
p=p->nxt[id];
}else{
p=p->nxt[id];
p->w++;//过该节点的字符串数量+1
}
}
p->v++;//最后一个字符打标机
}
inline int findTrie(int *str,int lenth){
int ans=0;
Trie *p=rot;
for(int i=0;i<lenth;i++){
int id=str[i];
p=p->nxt[id];//往下跳
if(p==NULL)//找不到完整的查询串
return ans;//只统计几个字典中字符串是查询串的前缀
ans+=p->v;//累加v
}
return p->w+ans-p->v;//不重不漏
}
int main(){
int n=read(),m=read();
for(int i=0;i<n;i++){
int st[maxn];
int len=read();
for(int j=0;j<len;j++)
st[j]=read();
createTrie(st,len);//建立字典树
}
int ans=0;
for(int i=0;i<m;i++){
int st[maxn];
int len=read();
for(int j=0;j<len;j++)
st[j]=read();
printf("%d
",findTrie(st,len));//输出查询结果
}
return 0;
}