A:不管有没有负数 一顿操作之后肯定只有正数 又因为A=A-B 所以最大值是一直在减小的 所以一定有结果
B:..一开始以为求min操作数 WA了2发 直接求所有数的GCD如果所有数的GCD都不是1的话就无解 有解就无脑扫2次就好了
C:给你一个char正方形矩阵 要求a[i][j]四个正方形对称轴都一样 可以任意change 直接爆搜八分之一块就行了.

#include <bits/stdc++.h> #include <cstring> #include <iostream> #include <algorithm> #define foror(i,a,b) for(i=a;i<b;i++) #define foror2(i,a,b) for(i=a;i>b;i--) #define EPS 1.0e-8 #define PI acos(-1.0) #define INF 3000000000 #define MOD 1000000007 #define mem(a,b) memset((a),b,sizeof(a)) #define TS printf("!!! ") #define lson o<<1, l, m #define rson o<<1|1, m+1, r //using ll = long long; //using ull= unsigned long long; //std::ios::sync_with_stdio(false); using namespace std; //priority_queue<int,vector<int>,greater<int>> que; int cmp(int a,int b) { return a<b; } char s[150][150]; int visit[150][150]; int gcd1(int a, int b) { return a == 0 ? b : gcd1(b % a, a); } map<char,int> mp; int main() { //freopen("in.txt", "r", stdin); //freopen("out.txt", "w", stdout); int t; cin >> t; while(t--) { int anser=0; int n; char ch; cin >> n; int mid=(n+1)/2; for(int i=1;i<=n;i++) mem(visit[i],0); for(int i=1;i<=n;i++) { scanf("%s",s[i]+1); } /*for(int i=1;i<=n;i++) { printf("%s ",s[i]+1); }*/ int maxn=0; for(int i=1;i<=(n+1)/2;i++) for(int j=1;j<=(n+1)/2;j++) { if(visit[i][j]==1) continue; if(i==j&&i+j==n+1) continue; if(i==j||i+j==n+1||2*i==n+1||2*j==n+1) { int ans=0; mp.clear(); mp[s[i][j]]++; mp[s[i][n+1-j]]++; mp[s[n+1-i][j]]++; mp[s[n+1-i][n+1-j]]++; mp[s[j][i]]++; mp[s[n+1-j][i]]++; mp[s[j][n+1-i]]++; mp[s[n+1-j][n+1-i]]++; visit[i][j]=1; visit[i][n+1-j]=1; visit[n+1-i][j]=1; visit[n+1-i][n+1-j]=1; visit[j][i]=1; visit[n+1-j][i]=1; visit[j][n+1-i]=1; visit[n+1-j][n+1-i]=1; ans=max(ans,mp[s[i][j]]); ans=max(ans,mp[s[i][n+1-j]]); ans=max(ans,mp[s[n+1-i][j]]); ans=max(ans,mp[s[n+1-i][n+1-j]]); ans=max(ans,mp[s[j][i]]); ans=max(ans,mp[s[n+1-j][i]]); ans=max(ans,mp[s[j][n+1-i]]); ans=max(ans,mp[s[n+1-j][n+1-i]]); //cout <<i << ""<<j<<endl; //cout<<4-ans/2<<endl; anser+=4-ans/2; } else { int ans=0; mp.clear(); mp[s[i][j]]++; mp[s[i][n+1-j]]++; mp[s[n+1-i][j]]++; mp[s[n+1-i][n+1-j]]++; mp[s[j][i]]++; mp[s[n+1-j][i]]++; mp[s[j][n+1-i]]++; mp[s[n+1-j][n+1-i]]++; visit[i][j]=1; visit[i][n+1-j]=1; visit[n+1-i][j]=1; visit[n+1-i][n+1-j]=1; visit[j][i]=1; visit[n+1-j][i]=1; visit[j][n+1-i]=1; visit[n+1-j][n+1-i]=1; ans=max(ans,mp[s[i][j]]); ans=max(ans,mp[s[i][n+1-j]]); ans=max(ans,mp[s[n+1-i][j]]); ans=max(ans,mp[s[n+1-i][n+1-j]]); ans=max(ans,mp[s[j][i]]); ans=max(ans,mp[s[n+1-j][i]]); ans=max(ans,mp[s[j][n+1-i]]); ans=max(ans,mp[s[n+1-j][n+1-i]]); //cout <<i << ""<<j<<endl; //cout <<8-ans<<endl; anser+=8-ans; } } cout << anser<<endl; } return 0; }
D:画人脸

#include <bits/stdc++.h> #include <cstring> #include <iostream> #include <algorithm> #define foror(i,a,b) for(i=a;i<b;i++) #define foror2(i,a,b) for(i=a;i>b;i--) #define EPS 1.0e-8 #define PI acos(-1.0) #define INF 3000000000 #define MOD 1000000009 #define mem(a,b) memset((a),b,sizeof(a)) #define TS printf("!!! ") #define lson o<<1, l, m #define rson o<<1|1, m+1, r //using ll = long long; //using ull= unsigned long long; //std::ios::sync_with_stdio(false); using namespace std; //priority_queue<int,vector<int>,greater<int>> que; char ans[11][1100][1100]; int len1[15],len2[15]; void init() { for(int i=0;i<8;i++) for(int j=0;j<8;j++) ans[3][i][j]='*'; ans[3][1][4]=ans[3][2][4]=ans[3][3][4]=' '; ans[3][1][3]=ans[3][2][3]=ans[3][3][3]=' '; ans[3][4][1]=ans[3][5][1]=ans[3][6][1]=' '; ans[3][4][6]=ans[3][5][6]=ans[3][6][6]=' '; ans[3][5][3]=ans[3][6][3]=' '; ans[3][5][4]=ans[3][6][4]=' '; len1[4]=1,len2[4]=3; for(int i=5;i<=10;i++) len1[i]=len1[i-1]*2+1; for(int i=5;i<=10;i++) len2[i]=len2[i-1]*2+1; } void draw1(int x,int x1,int y1,int x2,int y2)//y2>y1 x2>x1 { if(x1==x2) { for(int i=y1;i<=y2;i++) { ans[x][x1][i]='*'; } } else { for(int i=x1;i<=x2;i++) ans[x][i][y1]='*'; } } void draw(int x,int len) { int jian0=len>>1; int jianer=len>>3; int jianyi=len>>2; draw1(x,0,0,0,len-1); draw1(x,0,0,len-1,0); draw1(x,0,len-1,len-1,len-1); draw1(x,len-1,0,len-1,len-1); //TS; draw1(x,jianer,jianer,jianer+jianyi-1,jianer); draw1(x,jianer,jianer,jianer,jianer+jianyi-1); draw1(x,jianer+jianyi,jianer,jianer+jianyi,jianer+jianyi-1); draw1(x,jianer,jianer+jianyi-1,jianer+jianyi,jianer+jianyi-1); //TS; draw1(x,jianer,jianer+2*jianyi-1,jianer,jianer+3*jianyi-2); draw1(x,jianer,jianer+2*jianyi-1,jianer+jianyi,jianer+2*jianyi-1); draw1(x,jianer,jianer+3*jianyi-2,jianer+jianyi,jianer+3*jianyi-2); draw1(x,jianer+jianyi,jianer+2*jianyi-1,jianer+jianyi,jianer+3*jianyi-2); //TS; for(int i=len-1;i>=jian0;i--) for(int j=jianyi+jian0-1;j>=jianyi;j--) { ans[x][i][j]=ans[x-1][len-1-i][jianyi+jian0-1-j]; } //cout << x<<endl; } int main() { //freopen("in.txt", "r", stdin); //freopen("out.txt", "w", stdout); int n; init(); //TS; for(int x=4;x<=10;x++) { draw(x,1<<x); } while(scanf("%d",&n)==1) { if(n<8) break; int num=log2(n); for(int i=0;i<n;i++) { for(int j=0;j<n;j++) { printf("%c",ans[num][i][j]); } cout <<endl; } cout <<endl; } return 0; }
E:先离散化 离散化 +模拟双端队列

#include <iostream> #include <cstdio> #include <algorithm> using namespace std; struct Node{ int c,p; bool operator<(const Node& rhs)const{ if(c!=rhs.c) return c<rhs.c; return p<rhs.p; } }s[111111]; int N,K; int cal(int st,int ed){ int k=0,sum=0,ret=0; for(int p=st,q=st;q<=ed;){ if(k<=K){ sum++; ret=max(ret,sum); k+=s[q+1].p-s[q].p-1; q++; }else{ sum--; k-=s[p+1].p-s[p].p-1; p++; } } return ret; } int main() { // freopen("data.in","r",stdin); while(scanf("%d%d",&N,&K)==2){ int i,j; for(i=0;i<N;s[i].p=i++) scanf("%d",&s[i].c); sort(s,s+N); int ans=0; for(i=0;i<N;i=j+1){ int c=s[i].c; j=i; while(j+1<N && s[j+1].c==c) j++; ans=max(ans,cal(i,j)); } printf("%d ",ans); } return 0; }
F:递推DP
1)用dp[i][j]表示源串第i次操作后,与目标串不同的位置有几个。
(2)对于dp[i][j],有j个位置与目标串不同,所以可以将j个位置中的t个位置变为与目标串相同,把其余n-j个位置中的m-t个位置变为与目标串不同,转移方程就是dp[i+1][j-t+m-t]+=dp[i][j]*C(t,j)*C(m-t,n-j);
(3)如果j+m>n,那么t就无法从0开始枚举了,所以此时t从(m-(n-j))开始(m次操作中有n-j次操作落在n-j个相同位置的里面,还有m-(n-j)次操作落在j个不同位置的里面)。
(4)初始条件就是用cnt统计源串和目标串有多少个位置不一样,dp[0][cnt]=1,通过dp把路径都找出来,那么答案就是dp[k][0]。

#include <iostream> #include <cstdio> using namespace std; typedef long long LL; const LL MOD=1000000009; LL dp[111][111],c[111][111]; char s[111],d[111]; void _init(){ c[0][0]=1; for(int i=1;i<=100;i++){ c[i][0]=1; for(int j=1;j<=i;j++){ c[i][j]=(c[i-1][j-1]+c[i-1][j])%MOD; } } } int main() { int n,k,m, i,j,t,x; _init(); while(scanf("%d%d%d",&n,&k,&m)==3){ scanf("%s",s); scanf("%s",d); x=0; for(i=0;i<n;i++) if(s[i]!=d[i])x++; for(i=0;i<=k;i++) for(j=0;j<=n;j++) dp[i][j]=0; dp[0][x]=1; for(i=0;i<k;i++)//ith operation for(j=0;j<=n;j++){//j different if(dp[i][j]==0)continue; for(t=max(0,m-(n-j));t<=j&&t<=m;t++)//j+m should no biger than n or at least (m-(n-j)) should be change dp[i+1][j-t+m-t]=(dp[i+1][j-t+m-t]+dp[i][j]*c[j][t]%MOD*c[n-j][m-t]%MOD)%MOD; } LL ans=dp[k][0]; printf("%lld ",ans); } return 0; }
G:给你一个完全/非完全二叉树求最小的宽度 首先肯定把根节点的两个叶子放在同一侧是最优的 然后让较宽的那一枝在最里面是最优的 以一个节点为例:如果只有一个枝就无限地延伸 ans[x]=ans[a[x][0]] 如果有两个枝的话 相同就宽度+1 不同就取最大的

#include <bits/stdc++.h> #include <cstring> #include <iostream> #include <algorithm> #define foror(i,a,b) for(i=a;i<b;i++) #define foror2(i,a,b) for(i=a;i>b;i--) #define EPS 1.0e-8 #define PI acos(-1.0) #define INF 3000000000 #define MOD 1000000009 #define mem(a,b) memset((a),b,sizeof(a)) #define TS printf("!!! ") #define lson o<<1, l, m #define rson o<<1|1, m+1, r //using ll = long long; //using ull= unsigned long long; //std::ios::sync_with_stdio(false); using namespace std; //priority_queue<int,vector<int>,greater<int>> que; vector<vector<int> >a(10005); int ans[10005]; void doit(int x) { if(a[x].size()==0) { ans[x]=1; } else if(a[x].size()==1) { doit(a[x][0]); ans[x]=ans[a[x][0]]; } else if(a[x].size()==2) { doit(a[x][0]); doit(a[x][1]); if(ans[a[x][0]]==ans[a[x][1]]) ans[x]=ans[a[x][0]]+1; else ans[x]=max(ans[a[x][0]],ans[a[x][1]]); } } int main() { //freopen("in.txt", "r", stdin); //freopen("out.txt", "w", stdout); int n; while(scanf("%d",&n)==1) { mem(ans,0); for(int i=1;i<=n;i++) a[i].clear(); for(int i=1;i<=n-1;i++) { int x; scanf("%d",&x); a[x].push_back(i+1); } doit(1); /*for(int i=1;i<=n;i++) printf("%d ",ans[i]); cout << endl;*/ cout << ans[1]<<endl; } return 0; }
H:几何
题目大意:给你一个三角形的内切圆半径跟外接圆半径,求解出符合条件的三角形,输出三角形的三条边的长度,如果没有符合条件的三角形,输出“NO Solution!”。
解题思路:这个题是SP,既是因为情况不唯一,而且还有精度的误差。
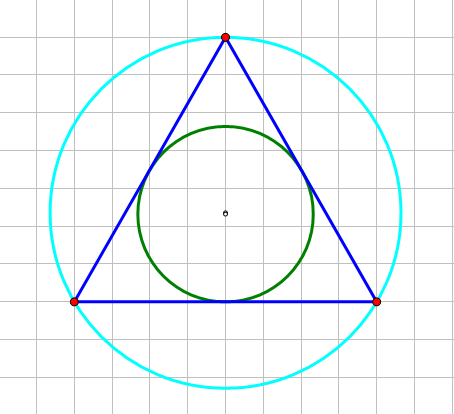
首先能够想到的就是NO Solution!的情况,即当内切圆半径等于1/2外接圆半径时,此时内切圆最大,而三角形为等边三角形,如图。
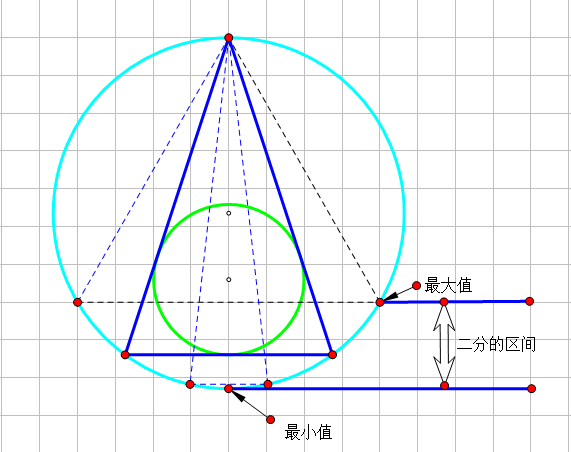
其次要解决的就是怎么构造三角形的问题,因为解不唯一,所以只要列举出一种解就OK,于是就很容易的想到构造等腰三角形,在最大与最小之间二分等腰三角形的底边长度,解三角形得到答案,如图。

#define sqr(x) (x)*(x) int main() { double r, R; while(~scanf("%lf%lf", &r, &R)){ if(R < 2*r){ printf("NO Solution! "); continue; } double left = 0, right = sqrt(3.0)*R; while(right-left > eps){ double mid = (left+right)/2.0; double t = sqrt(sqr(sqrt(sqr(R)-sqr(mid/2.0))+R)+sqr(mid/2.0)); //printf("%lf ", t); if(sqr(sqrt(sqr(r)+sqr(t-mid/2.0))+r) + sqr(mid/2.0) - sqr(t) < eps){ right = mid; } else { left = mid; } } double p = sqrt(sqr(sqrt(sqr(R)-sqr(left/2.0))+R)+sqr(left/2.0)); printf("%.16lf %.16lf %.16lf ", p, p, left); } return 0; } /*Sample test*/ /* */ ZOJ 3806
