Part 1:简单总结分治应用
分治算法不是一种固定的算法,确切的说,它是一种思想
总结一下几种常用的分治算法
二分法求解
注意事项
二分法在之前的分治博客中已经提到过了,这里仅作简单的补充描述
首先,二分法在求最优解问题上有广泛的应用,如果一个题目提到了“存在多个答案输出最优解”,那么有很大的概率要运用二分
其次,也是使用二分法需要注意的点:对于一个有单调性的答案区间,我们才能使用二分法进行求解
单调性:对于有解区间内的任意值(x_1,x_2(x_1<x_2)),带入求解得到解(y_1,y_2),那么(y_1,y_2)的大小关系一定可以确定
换句话说,就是解(y)关于自变量(x)的函数,在定义域(有解区间)内,具有单调性
二分法求解模板
使用(while)或者递归实现二分比较方便,这里因为个人习惯(while)就发一个(while)版本的(PS:递归有常数)
int l=/*二分下界,答案可能出现的最小值*/,r=/*二分上界,答案可能出现的最大值*/
while(l<=r){
int Mid=(l+r)>>1;
if(check(Mid)){
r=mid-1;//或者l=mid+1,看情况而定
//更新答案
}else l=Mid+1;
}
//最后的最优解是l
这里的(check())函数是精髓,需要根据题目来编写,用来判断这个解合不合法,然后缩小答案所在区间的范围,逐步求解
时间复杂度
一般是(O(klogn)),其中(k)是(check())函数的复杂度
分治法求解
其实二分属于分治,但是二分需要具有单调性,分治却不需要,所以这里才分开来讲
分治的应用范围非常广泛,对于一个大问题可以不断按照某种规则划分成几个小问题,而一些小问题可以直接求解的模型,可以考虑使用分治法
分治的典型应用就是各种(ex)数据结构(比如线段树、(st)表、二叉堆等等)
分治法模板
这个真的没啥模板了,就像(DP)方程一样,需要自己思考实现
Part 2:例题梳理
洛谷P1281书的复制
传送门
(Solution)
首先拿到了题面,扫了一眼之后发现了这样一句话很扎眼,而且出题人还单独分了一行出来给我们看:

嗯,求最大时间最少,有二分内味了
但是不能妄下结论,先判断一手单调性:
假设抄写页数最多的人花的时间是(x),那么显然其他人的抄写数量要(leq x)
因为其他人抄书数量在(leq x)时,不对答案造成影响,所以设所有人最多能抄书的页数为(y),那么(y)在当(x)增大时一定增大,当(x)减小时一定减小
换句话说,只要抄的总量不超过(x),每个人想抄多少抄多少,对答案没有影响。
为了所有人抄的总量最大,贪心的想,每个人要尽可能多抄,假设每个人都抄了(x),那么有(y=kx)((k)是人数),这个函数显然具有单调性
综上所述,本题可以使用二分法求解
明确了(y)与(x)之间的关系具有单调性,现在要求(x)的最小值,考虑二分(x)的值
每二分一次,我们都要检查一下这个答案是不是合法(也就是设计(check())函数)
题目中要求(k)个人去抄(m)本书,因为我们二分了(x)的值,所以每个人就最多抄(x)页
扫一遍整个代表每本书的页数的数组,如果一个人已经抄了(i)页,下一本书是(j)页
如果(i+jleq x)说明这个人再抄一本书也不会超过(x),根据每个人多抄的思路,我们把下一本书也给这个人抄
如果(i+j>x)说明这个人再抄下一本书,他就超过那个每个人最多抄(x)的限制了,此时我们要再新找一个人来抄这(j)页
扫到最后,看看这(k)个人在每个人抄写不超过(x)页的情况下能不能把所有书都抄完
如果抄不完,根据单调性,说明(x)取小了,如果抄完了,说明(x)可能取大了,更新答案,继续二分(x)
题目还要求后面的人多抄,那么我们只要在统计答案的时候,改为从后向前扫描,依旧贪心地分配任务(尽可能多抄)
二分结束后求出了最优的(x),再扫一遍整个数组,记录下每个人从第几本抄到第几本即为最终答案
(Code)
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<algorithm>
#include<set>
#include<map>
#include<utility>
#include<iostream>
#include<list>
#include<ctime>
#include<cmath>
#include<cstdlib>
#include<iomanip>
typedef long long int ll;
inline int read(){
int fh=1,x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-') fh=-1;ch=getchar(); }
while('0'<=ch&&ch<='9'){ x=(x<<3)+(x<<1)+ch-'0';ch=getchar(); }
return fh*x;
}
inline int _abs(const int x){ return x>=0?x:-x; }
inline int _max(const int x,const int y){ return x>=y?x:y; }
inline int _min(const int x,const int y){ return x<=y?x:y; }
inline int _gcd(const int x,const int y){ return y?_gcd(y,x%y):x; }
inline int _lcm(const int x,const int y){ return x*y/_gcd(x,y); }
const int maxn=505;
int seq[maxn];
struct Node{
int st,ed;
}wk[maxn];
int n,k,l,r; //l,r二分最快需要多少时间完成工作
inline bool check(const int Mid){
int t=0,cnt=0;//t记录这个人抄了t页,cnt记录用了cnt个人
for(int i=1;i<=n;i++){
if(t+seq[i]<=Mid) t+=seq[i];//合法,分配
else t=seq[i],cnt++;//超过了二分的值,新找一个人
if(cnt>k) return false;//如果用人数已经大于k个了,直接返回false
}
cnt++;//最后一点任务要分配一个人来抄
if(cnt<=k) return true;
else return false;
}
inline void make_ans(const int ans){//最终答案是ans,从后向前贪心分配每个人的工作
int t=0,cnt=k;//从后往前安排
wk[cnt].ed=n;//最后一个人的最后一本书是n
wk[1].st=1;//第一个人的第一本书是1
for(int i=n;i>=1;i--){
if(t+seq[i]<=ans) t+=seq[i];//抄第i本没有超过ans,贪心分配
else{
wk[cnt].st=i+1;//记录这个人抄到了第i+1本(因为是倒序枚举的)
cnt--;//找一个新的人
wk[cnt].ed=i;//新的人的最后一本书是第i本
t=seq[i];//新的人已经抄了i页
}
}
}
int main(){
n=read(),k=read();
for(int i=1;i<=n;i++){
seq[i]=read();
l=_max(l,seq[i]);
r+=seq[i];//更新答案区间上下界
}
while(l<=r){
int x=(l+r)>>1;//套板子
if(check(x)) r=x-1;
else l=x+1;
}
make_ans(l);//统计答案
for(int i=1;i<=k;i++)
printf("%d %d
",wk[i].st,wk[i].ed);
return 0;
}
平面最接近点对
传送门(1):洛谷P1429平面最接近点对(爸爸数据)
传送门(2):洛谷P1257平面最接近点对(儿子数据)
当然了这里教大家“打人先打脸,擒贼先擒王,骂人先骂娘”,我们直接拿爸爸开刀,如果切了爸爸,儿子就是双倍经验(爽)
(Solution)
不正确的做题姿势(1)
某数据结构巨佬:我喜欢暴力数据结构,所以我用(KD-Tree)的板子一边喝水一边过了此题(我要是出题人我马上给你卡成(O(n^2))的,让你装13)
不正确的做题姿势(2)
俗话说的好:“(n)方过百万,暴力碾标算,管他什么(SA),(rand()),能(AC)的算法就是好算法”
于是某玄学大师:“啊?我就按照(x)排了个序,如果要求最短,肯定横坐标差不会太大,所以我枚举每个点之前,之后的(10)个点,更新答案,然后就(AC)了……”
正确的做题姿势:
好习惯:打开题目看到数据范围——(nleq 2*10^5),猜到正解大概是一个复杂度为(O(nlogn))的算法
首先,题目随机给定(n)个点的坐标,先不管三七二十一,拿个结构体存下来一点也不亏
再考虑,如何更快的求解最小距离?突然想到了最小值具有结合律——即整个区间的最小值等于把它分成两个子区间,这两个子区间的最小值(比如线段树(RMQ))
但是现在手里的数组是无序的,这样没法划分区域,所以我们需要先排序,为了更直观些,我选择了按照横坐标(x)从小到大排序
假设我们有这样(5)个点,可以按照这(5)个点组成平面中,最中间的那个点,划分成左平面和右平面(中间点归左平面管)
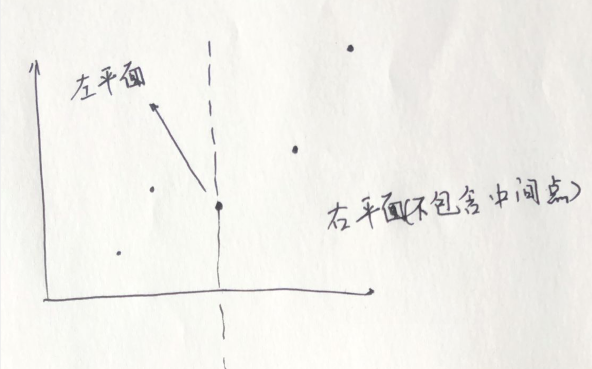
这样一直递归的划分下去,直到一个平面里只有(2)到(3)个点,此时我们暴力求出点距,然后向上合并平面统计(ans=min(ans,min(left,right));)
简直(Perfect),难道这题就这吗?显然不是,有一种情况被我们忽略了——产生最小点距的两个点可能来自不同的平面
现在处理这种特殊情况,设左平面和右平面中最接近点对的距离为(d),显然,只有横坐标与中间点横坐标距离不超过(d)的点才可能更新答案
形象点说,就是这样:
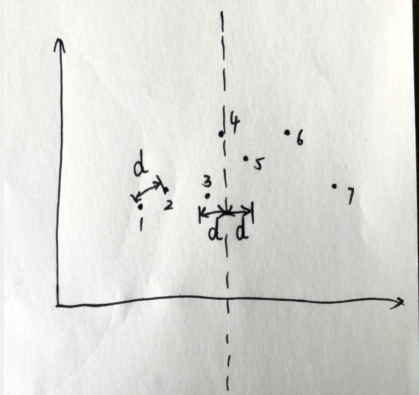
已知(d)的大小,如果一个左平面的点到中间点横坐标的距离已经(>d),那么它想和右边的点结合,此时两点距离一定(>d),不可能更新答案,对于右平面也是这样
所以对于上图,我们只用枚举(3、4、5),也就是与中间点(4)横坐标距离小于等于(d)的点即可
但是这么做,复杂度仍然有可能退化到(O(n^2)),因为可能有这种数据:
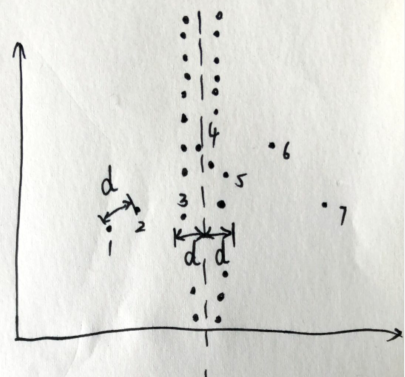
当卡在判断距离之内的点过多时,这么做其实和纯种的暴力没有区别了,怎么办呢?(但是对于这个题来说已经足够了,吸个氧就过掉了)
发动人类智慧精华:既然我们可以按照横坐标排序划分,为什么不能按纵坐标排序划分呢?
我们先(O(n))把距离中间点横坐标距离(leq d)的点全都统计出来到一个数组(T)里,然后把数组(T)按照纵坐标排序
那么我们找可能更新答案的点对时,还可以以纵坐标作为约束,这样,根据某玄学的数学证明方法(鸽巢原理),枚举次数不会超过(6)?
这样再更新一次答案,不停合并直到得到整个平面的最接近点对即可
Code
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<algorithm>
#include<set>
#include<map>
#include<utility>
#include<iostream>
#include<list>
#include<ctime>
#include<cmath>
#include<cstdlib>
#include<iomanip>
typedef long long int ll;
inline int read(){
int fh=1,x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-') fh=-1;ch=getchar(); }
while('0'<=ch&&ch<='9'){ x=(x<<3)+(x<<1)+ch-'0';ch=getchar(); }
return fh*x;
}
inline int _abs(const int x){ return x>=0?x:-x; }
inline int _max(const int x,const int y){ return x>=y?x:y; }
inline int _min(const int x,const int y){ return x<=y?x:y; }
inline int _gcd(const int x,const int y){ return y?_gcd(y,x%y):x; }
inline int _lcm(const int x,const int y){ return x*y/_gcd(x,y); }
inline double _dis(const double x1,const double y1,const double x2,const double y2){
return std::sqrt(std::pow(x1-x2,2)+std::pow(y1-y2,2));
}
inline double _smin(const double a,const double b,const double c){ return std::min(a,std::min(b,c)); }
const int maxn=200005;
struct Node{
double x,y;
}poi[maxn];
inline bool cmd1(const Node a,const Node b){ return a.x<b.x; }
inline bool cmd2(const Node a,const Node b){ return a.y<b.y; }
int n;
double find(const int L,const int R){
if(R==L+1) return _dis(poi[L].x,poi[L].y,poi[R].x,poi[R].y);
if(R==L+2) return _smin(_dis(poi[L].x,poi[L].y,poi[L+1].x,poi[L+1].y),_dis(poi[L+1].x,poi[L+1].y,poi[R].x,poi[R].y),_dis(poi[L].x,poi[L].y,poi[R].x,poi[R].y));
//点数<=3暴力统计
int Mid=(L+R)>>1;//按x二分平面
double d=std::min(find(L,Mid),find(Mid+1,R));//找最小值
int cnt=0;
Node T[1005];
for(int i=L;i<=R;i++)
if(poi[i].x>=poi[Mid].x-d&&poi[i].x<=poi[Mid].x+d){
T[++cnt].x=poi[i].x;
T[cnt].y=poi[i].y;
}//O(n)统计所有可能更新答案的点
std::sort(T+1,T+cnt+1,cmd2);//按y排个序
for(int i=1;i<=cnt;i++)//枚举所有可能更新答案的点
for(int j=i+1;j<=cnt;j++){
if(T[j].y-T[i].y>=d) break;//如果纵坐标之差超过d,显然不可能更新答案,跳出
d=std::min(d,_dis(T[i].x,T[i].y,T[j].x,T[j].y));//尝试更新答案
}
return d;//返回平面最小值d
}
int main(){
n=read();
for(int i=1;i<=n;i++)
poi[i].x=read(),poi[i].y=read();//读入点对
std::sort(poi+1,poi+n+1,cmd1);//按照x排序
double ans=find(1,n);
printf("%.4lf",ans);//lf精度别忘了
return 0;
}