NLP与深度学习（四）Transformer模型

1. Transformer模型

在Attention机制被提出后的第3年，2017年又有一篇影响力巨大的论文由Google提出，它就是著名的Attention Is All You Need^[1]。这篇论文中提出的Transformer模型，对自然语言处理领域带来了巨大的影响，使得NLP任务的性能再次提升一个台阶。

Transformer是一个Seq2Seq架构的模型，所以它也由Encoder与Decoder这2部分组成。与原始Seq2Seq 模型不同的是：Transformer模型中没有RNN，而是完全基于Attention（以及全连接层）。在大型数据集上，它的效果可以完全碾压RNN模型（即使RNN中加入Attention机制）。现如今例如机器翻译场景，已经看不到RNN的影子了，基本都是Transformer + Bert。

Transformer模型的架构如下图所示：

 

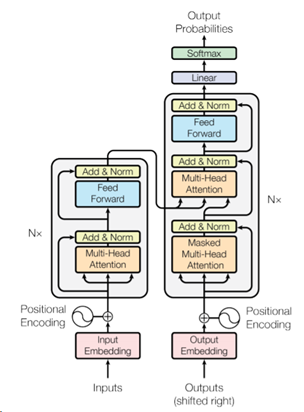
Figure 1: The Transformer - model architecture^[1]

在上图中，左边的是Encoder部分，右边的是Decoder部分。它们旁边均有个Nx，这个代表的是有N个这个的结构层进行堆叠，这里N为6。假设左边与右边部分命名分别为Base_Encoder_Layer和Base_Decoder_layer（均抛开Input Embedding与Positional Encoding），则Encoder由Base_Encoder_Layer堆叠6次组成，Decoder是由Base_Decoder_layer堆叠6次组成。

由于Transformer也是Seq2Seq模型，所以它们的输入输出与流程基本一致。在Transformer中，输入首先经过词嵌入（Word Embedding）以及（Positional Encoding），然后输入到6个堆叠的Base_Encoder_Layer中，得到隐藏层的向量表示h。然后在Decoder中，隐藏层向量h会输入到每个Base_Decoder_Layer。Decoder的输入经过6个堆叠的Base_Decoder_Layer后，得到Decoder的输出。此过程如下图所示（此图是一个基本流程，省去了很多组件）：

 

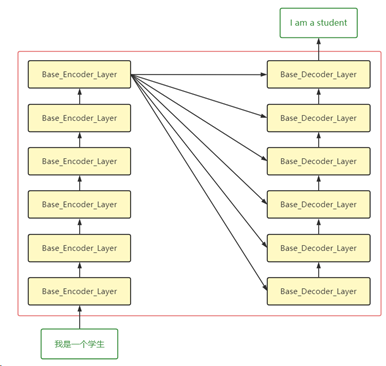
在对Transformer模型有了一个基本了解后，下面逐一介绍Transformer中的各个组件。

2. Input Embedding

与其他序列转换模型一样，Transformer使用了预训练的词嵌入，将输入的单词（Input Embedding层）以及输出的单词（Output Embedding层）转为512维的词嵌入。词嵌入的介绍以及方法已经在前面（NLP与深度学习（一）NLP任务流程）已经介绍过，在此不再赘述。不过值得提到的一点是：如果训练的数据非常大，那么使用随机初始化的词向量与预训练的词向量（如word2vec、GloVe）的结果差别不会太大。但如果是参加各类比赛的话，则需要多尝试各种方法。

2. Positional Encoding

前面提到，Transformer模型种没有使用RNN，而是完全基于Attention。RNN的一个重要特点就是：对于输入序列的单词是有位置信息的。例如“我爱中国“，第一个输入字符是”我“，然后是”爱“，直到最后的”国“。所以RNN在处理序列过程种本身就包含了输入字符的位置信息。但是这种机制在Attention中是没有的，所以Transformer在处理输入序列时，需要对输入序列的每个token进行位置编码。

在原论文中，位置编码的公式为：

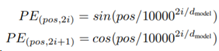
首先解释公式里的3个参数：

1. pos：序列中token（也就是单词）的位置
2. i：词向量的维度范围。例如假设词向量维度为512，则i的范围为[0, 511]
3. d_model：Embedding维度，论文中为512维

然后可以看到编码公式一共有2个，分别定义了偶数位置（2i）与奇数位置（2i+1）的位置i的编码方式。偶数位置i的值使用sin函数，奇数位置的i的值使用cos函数。

下面举个例子说明编码方式，以“我爱我的国家“序列为例。其中”爱“在序列中的位置为1（从0开始），维度为512（词嵌入维度）。所以”爱“的位置编码为：

PE_{(1, 2i)} = sin(1/10000^2i/512)

PE_{(1, 2i+1)} = cos(1/10000^2i/512)

将sin与cos方法抽象出来后，更具体的表现为：

爱 => 512维词嵌入 [0, 1, 2, …, 511]  => 对不同位置i的值进行处理 [sin, cos, sin, …, cos]

如下图所示：

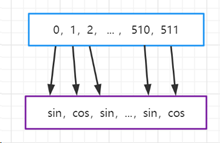
所以最终对单词“爱“的位置编码也为512维（与词嵌入维度一致）。在得到一个单词的位置编码PE_token后，直接与单词的Embedding_token进行矩阵加法，即完成了对输入单词的编码。

在原论文中，作者还提到了另一种位置编码的方法：直接通过训练学习得到位置编码。并且从测试结果来看，两者几乎没什么差别。不过作者最终仍使用了正弦曲线（sin与cos）的方法，原因有2点：

1. 因为它可以使得模型能够适应更长的序列。举个例子，假设训练集中序列最长长度为100，但是在部署后遇到了长度为110的序列。正弦曲线的方法在这种情况下仍能很好的以预期的方式对序列进行位置编码。
2. 预期模型能够很容易学习到相对位置的表示。因为任意位置的PE_pos+k 都可以被PEpos 以线性函数的方式表示。这点基于的是2个公式：cos(a + b) = cos(a)cos(b) – sin(a)sin(b) 和 sin(a + b) = sin(a)cos(b) + cos(a)sin(b)

在输入经过了词嵌入与位置编码后，下一步遍输入Encoder进行处理。

3. Base_Encoder_Layer

前面提到Encoder是由6个Base_Encoder_Layer堆叠而来（这里Base_Encoder_Layer是本文为了方便解释而提出，并非原论文中的术语），其中每个Base_Encoder_Layer的结构都相同，如下图所示：

 

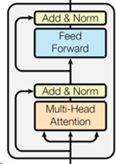
在每个Base_Encoder_Layer中，都由2个Sublayer组成，分别为多头自注意力机制（Multi-Head Self-Attention mechanism），以及一个前馈网络（Feed Forward）。而每个Sublayer都使用了残差连接（residual connection）以及层标准化（Layer Normalization）。

使用公式来表示，每个Sublayer的输出Sublayer_Output即可表示为：

Sublayer_Output = LayerNorm(x + Sublayer(x))

残差连接与层标准化LN（Layer Normalization）均是用于在模型到一定深度后，为了解决梯度消失的问题而提出（相对于层标准化，还有批标准化BN（Batch Normalization），但是BN在NLP场景有局限性）。这2部分不在本文的讨论中，所以不在此进行赘述。

下面我们介绍Base_Encoder_Layer中最重要的部分——多头自注意力机制。

4. Multi-Head Self-Attention

在介绍多头自注意力（Multi-Head Self-Attention）机制前，我们先介绍Self-Attention。

4.1. Self-Attention

在上一章中，我们介绍了注意力（Attention）机制，它被应用于Seq2Seq模型中，解决长序列的表示问题。在每一个时间步t中，在计算Attention时，除了需要当前Decoder在时间步t的输入外，还需要用到所有输入序列的hidden states。这个是一般Attention的计算方法。但是在Self-Attention中，并不需要Decoder的输入，而是仅用Encoder的输入。

首先我们要明确一个概念：Self-Attention是输入一个序列，输出一个同等长度的序列。输出序列中每个输出token，都是看过了输入序列中每个输入token的信息后生成 。如下图所示：

 

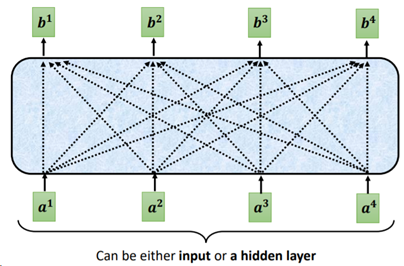
Fig. 2. 李宏毅. Transformer Model^[2]

Self-Attention中涉及到3个可训练的参数矩阵，分别为W_K，W_Q与W_V。假设输入的序列为x=[x₁, x₂, …, x_m]，使用512维的词嵌入，则x向量的维度为[m, 512]（在batch训练时，维度应为[batch, m, 512]）。在这个前提下，计算Self-Attention的具体步骤为：

1. 对每个输入token x_i，分别与参数矩阵W_K，W_Q与W_V 进行矩阵乘法。这3个参数矩阵的维度均为[dim_Embedding, d]（其中d = d_K = k_Q = d_V = 64），在原论文中是[512, 64]。得到3个向量分别为：

l  Query向量Q=[q₁, q₂, …, q_m]，维度为[m, 64]

l  Key向量K = [k₁, k₂, …, k_m]，维度为[m, 64]

l  Value向量V = [v₁, v₂, …, v_m]，维度为[m, 64]

以x₁为例（维度为[1, 512]），分别与W_K，W_Q与W_V做矩阵乘法得到的向量为q₁，k₁，v₁，维度均为[1, 64]。如下图所示：

 

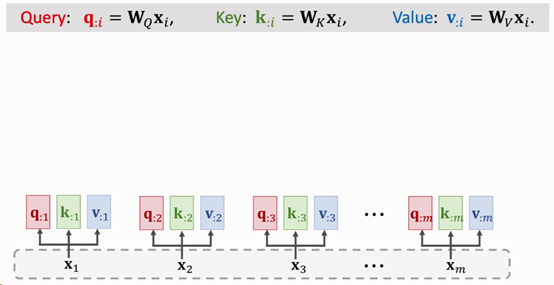
Fig. 3. ShusenWang. Transformer Model^[3]

1. 然后计算权重向量a。对每个q_i（维度为[1, 64]）与K向量（维度为[m, 64]）每一行进行点积（其实就是与每个k_i做点积），也就是[q_i * k₁, q_i * k₂, …, q_m * k_m]。得到向量a₁（维度为[1, m]），并将a_i送入Softmax后得到权重向量a_i（维度为[1, m]）。最终得到权重向量a = [a₁, a₂, …, a_m]（维度为[m, m]）。如下图所示：

 

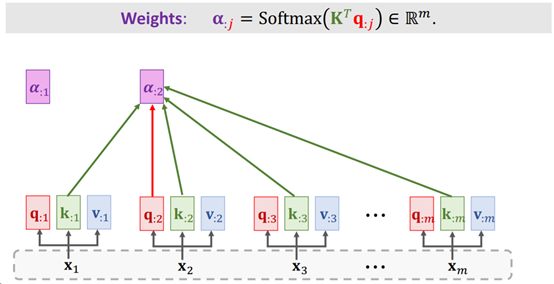
Fig. 4. ShusenWang. Transformer Model^[3]

3. 对每个v_i（维度为[1, 64]），与其对应的a_i权重（维度为[1, m]）进行加权平均（此时a_i即为v_i的权重），得到上下文向量c_i，即c_i =v₁ * a₁ + v₂ * a₂ +…+ v_m * a_m（维度为[1, 64]）。并最终得到Self-Attention的输出，也就是上下文向量c=[c₁, c₂, …, c₃]，维度为[m, 64]。如下图所示：

 

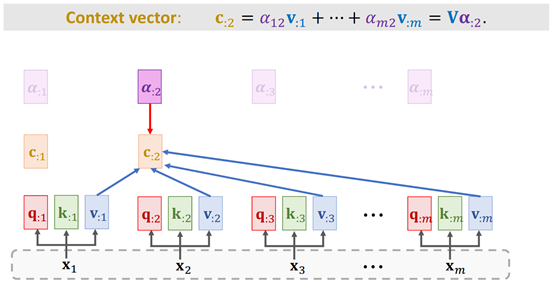
Fig. 5 ShusenWang. Transformer Model^[3]

整个过程用公式表示很简单：

Attention(Query, Key, Value) = softmax(Query x Key^T) x Value

但是在Transformer中，对Query x Key^T 进行了进一步缩放，使用的公式为：

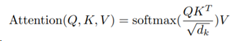
其中d_k = d_v = d_model/h = 64。这里h表示的Multi-Head的个数，原模型中为8。前面提到过，d_model为512。

所以在经过了1个Self-Attention层后，输入由[m, 512] 转变为了[m, 64]。且每个c_i都包含了每个输入x_i的信息。这篇文章中^[4]也很清晰地展示了这个计算过程：

 

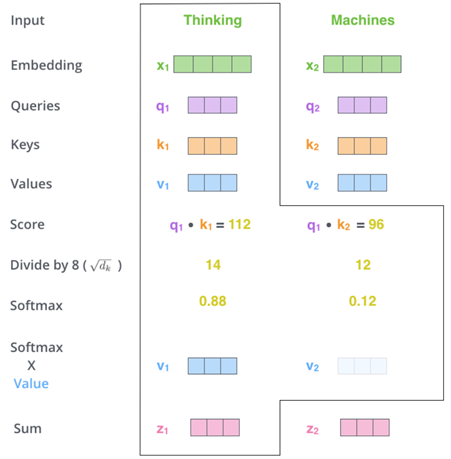
Fig.6. Jay Alammar. The Illustrated Transformer^[4]

在了解了Self-Attention的计算方法后，下面我们继续介绍Multi-Head Self-Attention。

4.2. Multi-Head Self-Attention

多头自注意力机制（Mutli-Head Self-Attention）其实非常简单，就是多个Self-Attention的输出的拼接。如下图所示：

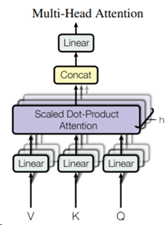
例如，transformer中使用的是8头（也就是图中的h=8），那就有8个self-attention模块。这8个self-attention的W_K，W_Q，W_V 参数均不共享。也就是说，会有8组不同的W_K，W_Q，W_V 参数。

前面提到，在经过了1个Self-Attention层后，输入由[m, 512] 转变为了[m, 64]。那同时经过8-头Self-Attention后，将所有Self-Attention的输出进行拼接，输出维度即为[m, 512]（也就是 64 * 8 = 512）。

5. Encoder总结

前面提到，每个Base_Encoder 中都有2个Sublayer，1个为Multi-Head Attention，1个为前馈网络（Feed Forward Network，其实就是一个全连接层）。每个Sublayer的输出Sublayer_Output即可表示为：

Sublayer_Output = LayerNorm(x + Sublayer(x))

在经过6个Base Encoder的堆叠后，便得到了Encoder的输出u=[u₁, u₂, …, u_m]，维度为[m, 512]。如下图所示：

 

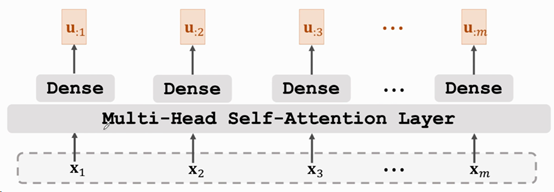
Fig. 7 ShusenWang. Transformer Model^[3]

它会输入到每个Base_Decoder_Layer中进行进一步处理。

6. Decoder

同样，Decoder部分也是由6个Base_Decoder_Layer堆叠而来（这里Base_ Decoder _Layer同样也是本文为了方便解释而提出，并非原论文中的术语），其中每个Base_ Decoder _Layer的结构都相同，如下图所示（需要注意的是，Base_Decoder_Layer仅代表Nx的那部分，前后的输入与输出不包含在这个堆叠结构中）：

 

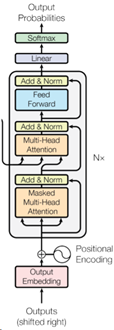
6.1. Decoder 输入

在Decoder中，首先来看输入部分，可以看到这里有个shifted right，这里表示右移一位。是为了在给Decoder第一次输入时，添加一个起始符。因为Decoder在第一次输入时，需要一个起始符。以机器翻译为例，将中文翻译为英文。Encoder输入是“我爱中国”。在对应Decoder输出时，它需要一个起始的状态，例如</start>，将其编码后，输入到Decoder中，而后模型应该输出一个“I”。然后“love”再次作为Decoder的输入，用于预测下一个单词。所以正常的Decoder输出序列应为：

0 – “I“

1 – “love”

2 – “China”

而在Decoder的输入序列应为：

0 – “</start>”

1 – “I“

2 – “love”

3 – “China”

所以相当于输出整体右移了1位。

然后便是与Encoder部分同样结构的Embedding（这个Embedding层与Encoder中Embedding层共享同一组词嵌入参数）以及Positional Embedding，在此不再赘述。

6.2. Base_Decoder_Layer

Base_Decoder_Layer的结构与Base_Encoder_Layer中sublayer的结构类似，里面包含3个Sublayer。首先是一个Masked Multi-Head Self Attention层，它与前面提到的Multi-Head Self Attention稍微有点区别。

在Encoder 中，由于序列是一次性输入的，所以在计算Multi-Head Self Attention时，可以获取到所有的输入信息。但是在Decoder中，只能看到当前已经输出的序列信息。以机器翻译为例，Encoder输入是“我爱中国“。预期Decoder的输入应为”I love China“。但是在时间步1时，Decoder输入了”love“，所以此时Decoder在计算Multi-Head Self Attention时，仅能看到”I love“这2个单词。所以此时便引入了Masked Multi-Head Self Attention。

Masked Multi-Head Self Attention 与 Multi-Head Self Attention的计算方法类似，也是使用了3个参数矩阵W_K，W_Q与W_V。它们唯一的区别在于计算权重向量a那里。例如，在第2个时间步t₂时，由于Decoder仅能看到输入的x₁与x₂，所以在计算权重向量a₁时，只会使用到x₁与x₂，如下图所示（需要注意的是，Decoder的输出并非是一个序列，而是每次一个单词，也就是说，这里t₂时间步的输出此时只有c₂）：

 

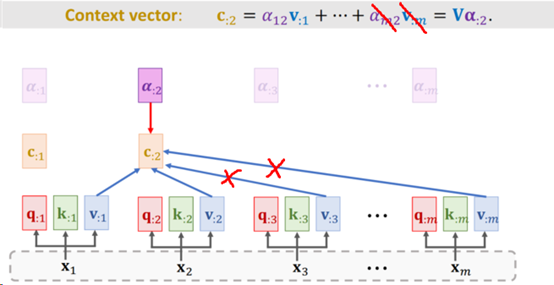
在得到Masked Multi-Head Self Attention的输出后（维度为[1, 512]）。继续进入到下一个

Multi-Head Self Attention。但是在这一层的Multi-Head Self-Attention中，Encoder的输出也会加入进来，如下图所示：

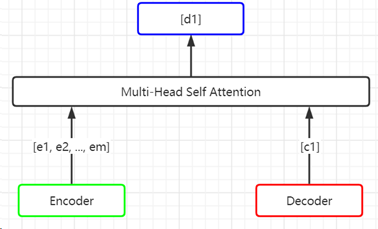
Encoder部分e的维度为[m, 512]，Decoder输入部分c1的维度为[1, 512]，经过Multi-Head Self-Attention后，输出为d1，维度为[1,512]。最后，d1会输入到一个前馈网络。这样，一个Base_Decoder_Layer便结束了。将6个Base_Decoder_Layer进行堆叠，得到的向量（维度为[1, 512]）输入到一个线性变化层（Linear，就是一个全连接神经网络），然后输入到softmax后，即可进行根据softmax输出的概率结果，对下一个单词进行预测。

7. Transformer总结

Transformer模型的出现，对NLP领域产生了巨大的影响。当前仍非常热门的预训练模型如BERT（仅使用了Transformer的Encoder部分），GPT-2，GPT-3（GPT使用的是Decoder部分）等，都是基于Transformer模型而构建。对于小型企业或是各类比赛，这几个预训练模型（及其变种）仍然在被广泛使用。后续我们会介绍BERT与GPT以及它们的应用。

References

[1] https://arxiv.org/pdf/1706.03762.pdf

[2] https://www.bilibili.com/video/BV1Wv411h7kN?p=35

[3] https://www.bilibili.com/video/BV1SK4y1d7Qh

[4] http://jalammar.github.io/illustrated-transformer/

[5] https://www.zhihu.com/question/337886108/answer/893002189